1. Определение и свойства плотности распределения.

Определение плотности распределения

Выше непрерывная случайная величина задава­лась с помощью функции распределения. Этот способ задания не является единственным. Непрерывную слу­чайную величину можно также задать, используя другую функцию, которую называют плотностью распределения или плотностью вероятности (иногда ее называют диф­ференциальной функцией). .

Плотностью распределения вероятностей непрерывной

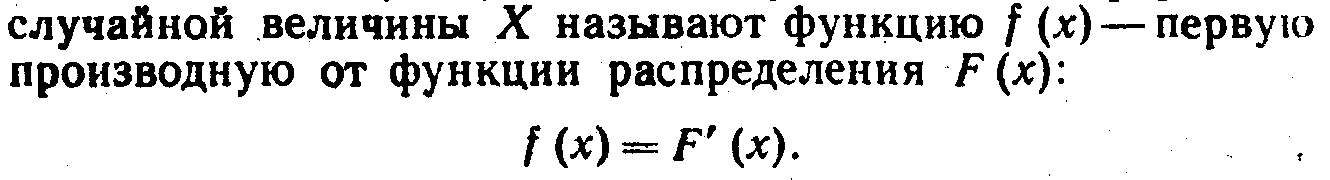
Из этого определения следует, что функция распре­деления является первообразной для плотности распре­деления.

Заметим, что для описания распределения вероятно­стей дискретной случайной величины плотность распре­деления неприменима.

Свойства плотности распределения

Свойство 1. Плотность распределения—не­отрицательная функция:

Доказательство. Функция распределения — не­убывающая функция, следовательно, ее производная

Рис. 1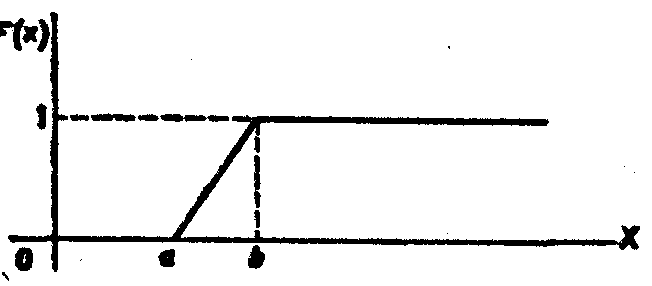

отрицательная.

Геометрически это свойство означает, что точ­ки, принадлежащие гра­фику плотности распреде­ления, расположены либо над осью Ох, либо на этой оси.

График плотности распределения называют кривой распределения.

Свойство 2. Несобственный интеграл от плотности распределения в пределах от - ∞ до + ∞ равен единице:

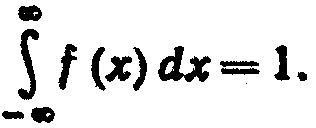
Доказательство. Несобственный интеграл

том, что случайная величина примет значение, принад-

достоверно, следовательно, вероятность его равна единице.

Геометрически это означает, что вся площадь криво­линейной трапеции, ограниченной осью Ох и кривой распределения, равна единице.

В частности, если все возможные значения случайной величины принадлежат интервалу (а, b), то

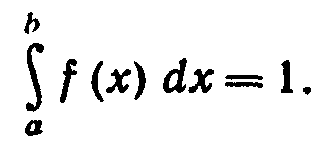
Пример. Плотность распределения случайной величины Х задана:

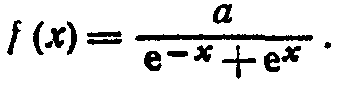
Найти постоянный параметр а.

Решение. Плотность распределения должна удовлетворять ус-

венство

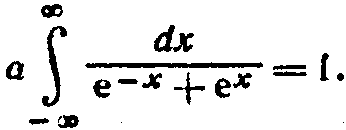
Отсюда

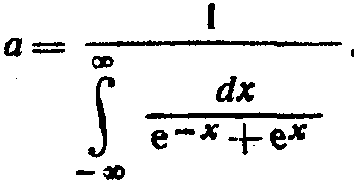
Найдем неопределенный интеграл:

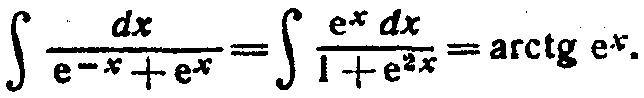
Вычислим несобственный интеграл:

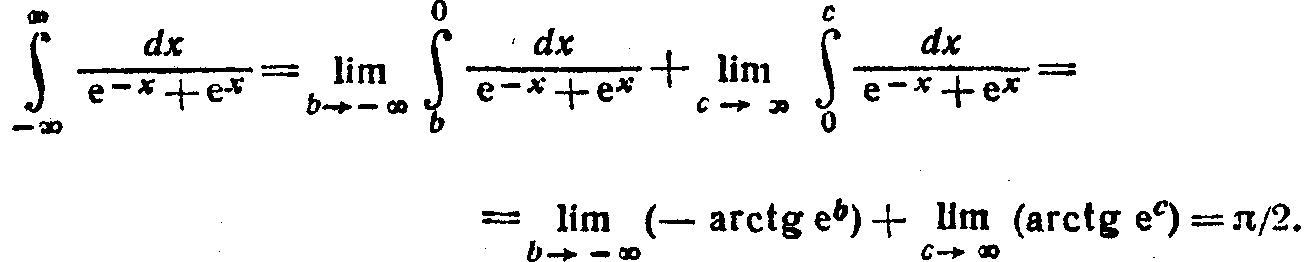
Таким образом, искомый параметр

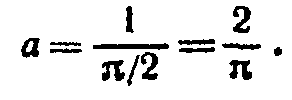
2. Взаимосвязь функции и плотности распределения вероятностей.

Зная плотность распределения f (x), можно найти функцию распределения F (x) по формуле

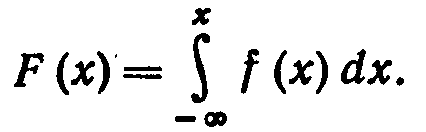
Действительно, мы обозначили через F (x) вероятность того, что случайная величина примет значение, мень­шее x. т. е.

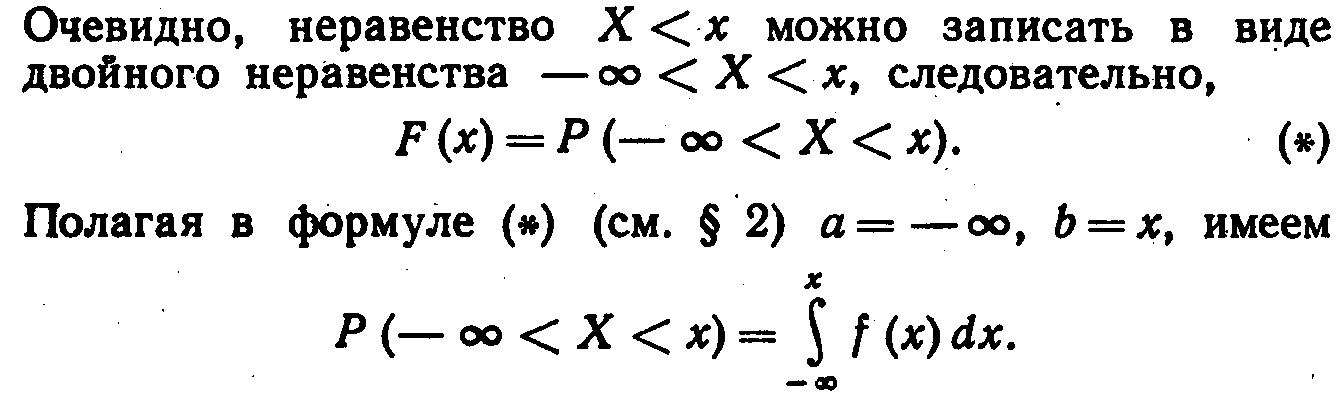
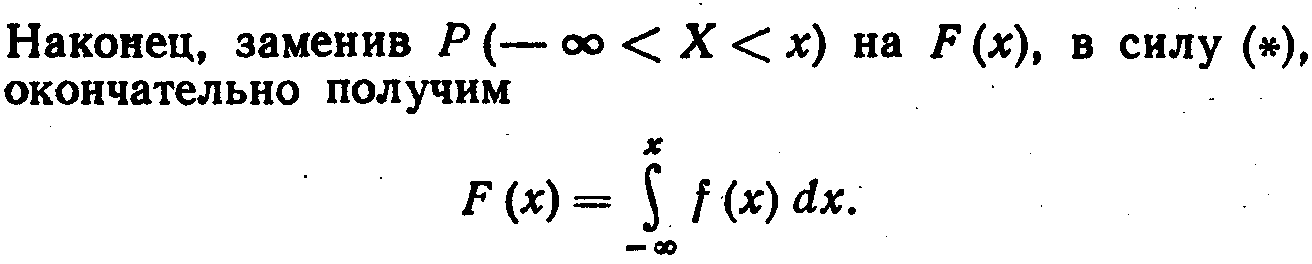
Таким образом, зная плотность распределения, можно найти функцию распределения. Разумеется, по известной функции распределения может быть найдена плотность распределения, а именно:

Пример. Найти функцию распределения по данной плотности распределения:

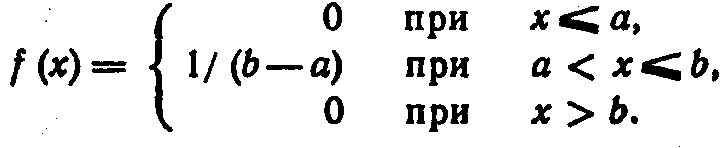
Построить график найденной функции.

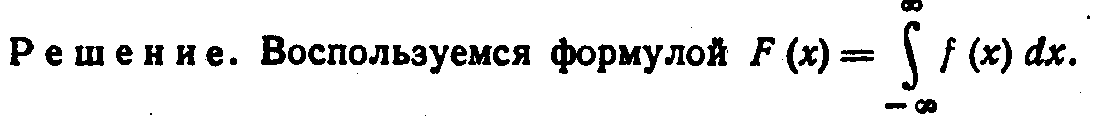
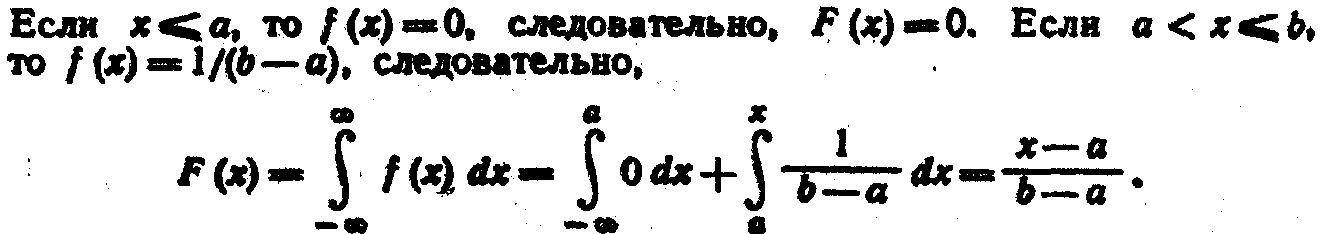
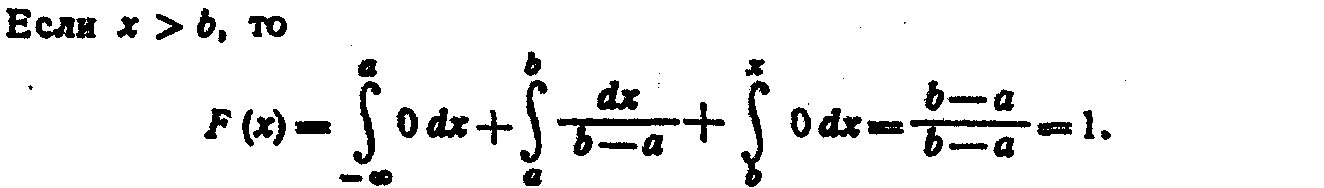
Итак, искомая функция распределения

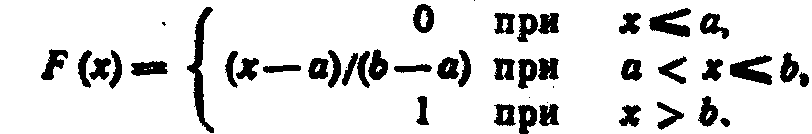
График этой функции изображен на рис. 1.

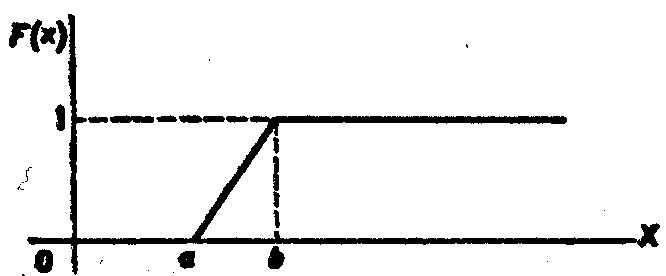
Рис. 1.

3. Вероятностный смысл плотности распределения.

Пусть F (x)—функция распределения непрерыв­ной случайной величины X. По определению плотности

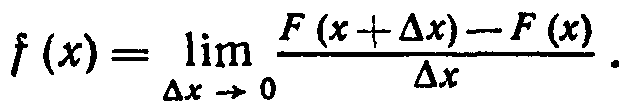
деляет вероятность того. что Х примет значение, при-

дел отношения вероятности того, что непрерывная слу­чайная величина примет значение, принадлежащее интер­

равен значению плотности распределения в точке x. По аналогии с определением плотности массы в точке *)

----------------------------------------------------------------------------------------------

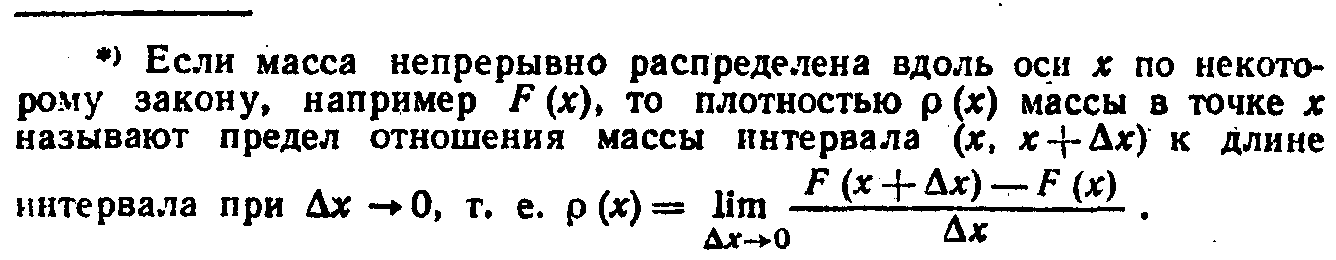
точке х как плотность вероятности в этой точке.

Итак, функция f (х) определяет плотность распределе­-

ния вероятности для каждой точки х.

Из дифференциального исчисления известно, что при­ращение функции приближенно равно дифференциалу функции, т. е.

или

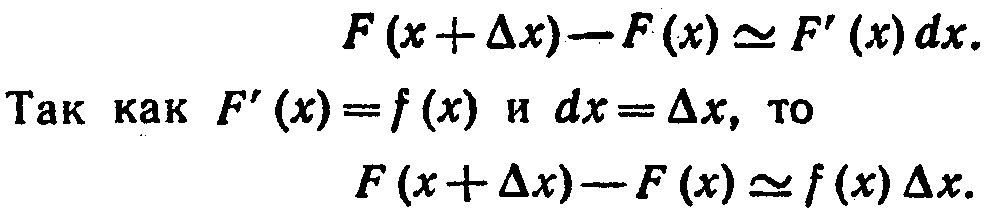
Вероятностный смысл этого равенства таков: вероят­ность того, что случайная величина примет значение.

(с точностью до бесконечно малых высшего порядка от-

Геометрически этот результат можно истолковать так:

вероятность того. что случайная величина примет значение принадлежащее интервалу (х ,х+∆х ),приближенно

равна площади прямоуголь­ника с основанием ∆х и вы­сотой f(x).

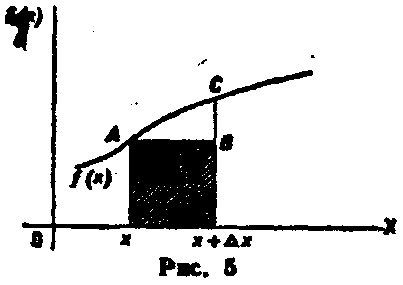
На рис. 5 видно, что пло­щадь заштрихованного пря­моугольника, равная произве-

женно равна площади криво­линейной трапеции (истинной вероятности, определяемой определенным интегралом

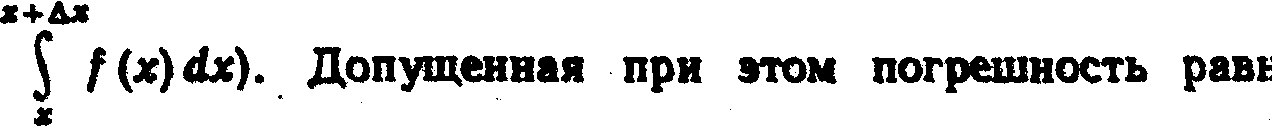
площади криволинейного треугольника АВС.