4 . Распределение Пуассона

Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А равна р. Для определения вероятности k появлений со­бытия в этих испытаниях используют формулу Бернулли. Если же п велико, то пользуются асимптотической фор­мулой Лапласа. Однако эта формула непригодна, если вероятность события мала (Р≤0,1). В этих случаях (п велико, р мало) прибегают к асимптотической формуле Пуассона.

Итак, поставим перед собой задачу найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно k раз.

Сделаем важное допущение: про­изведение пр сохраняет постоянное значение, а именно пр=λ. Как будет следовать из дальнейшего, это означает, что среднее число появлений события в различных сериях испытаний, т. е. при различных значениях п, остается неизменным.

Воспользуемся формулой Бернулли для вычисления, интересующей нас вероятности:

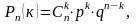но т.к. из формул комбинаторики известно, что число размещений 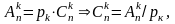при этом 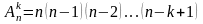. Тогда можно записать:

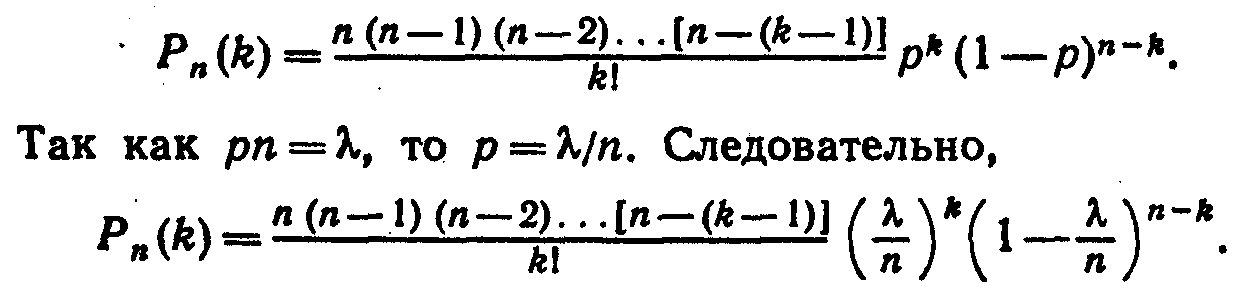
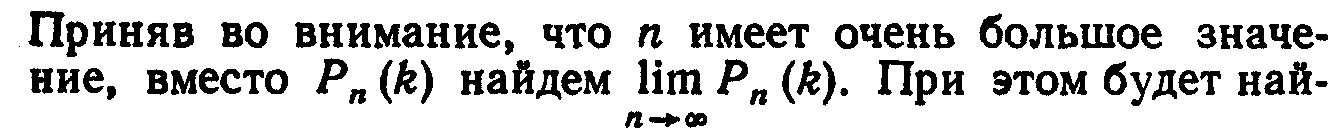
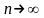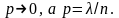дено лишь приближенное значение отыскиваемой вероят­ности; п хотя и велико, но конечно, а при отыскании предела мы устремим п к бесконечности. Заметим, что поскольку произведение пр сохраняет постоянное значение, то при , вероятность Причём

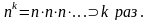
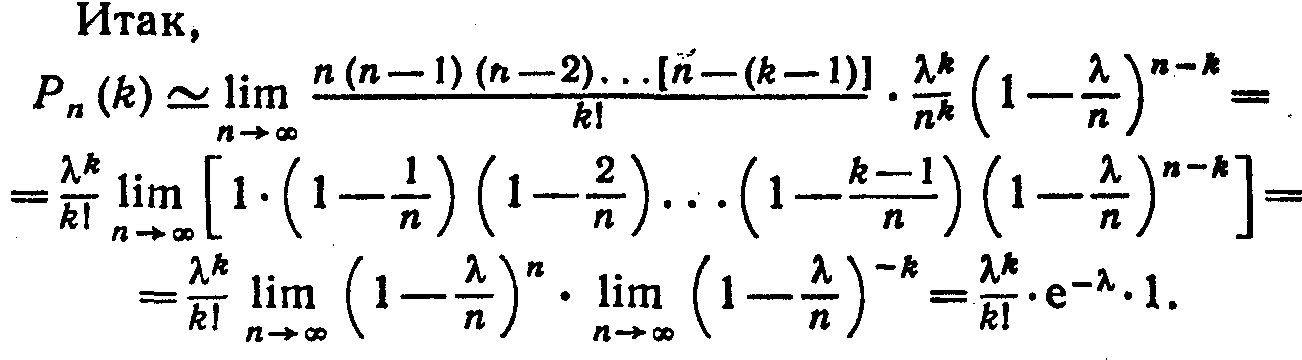
. Таким образом (для простоты записи знак приближен­ного равенства опущен):

Эта формула выражает закон распределения Пуассона вероятностей массовых (п велико) и редких (р мало) событий.

Замечание. Имеются специальные таблицы, пользуясь кото­рыми можно найти Pn(к), зная k и λ.

Пример. Завод отправил на базу 5000 доброкачественных изде­лий. Вероятность того, что в пути изделие повредится, равно 0,0002. Найти вероятность того. что на базу прибудут 3 негодных изделия.

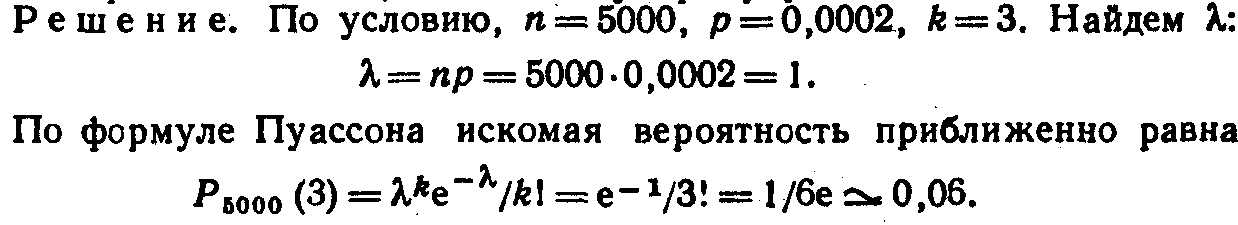
5 . Геометрическое распределение .

Пусть производятся независимые испытания, в каждом из которых вероятность появления события А

только появится событие А. Таким образом, если собы­тие А появилось в к-м испытании, то в предшествующих k—1 испытаниях оно не появлялось.

Обозначим через Х дискретную случайную величину — число испытаний, которые нужно провести до первого появления события А. Очевидно, возможными значе-

сложного события», по теореме умножения вероятностей независимых событий,

По этой причине распределение (*) называют геометри­ческим.

Легко убедиться, что ряд (**) сходится и сумма его равна единице. Действительно, сумма ряда (**)

Пример. Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель р== 0,6. Найти вероятность того, что попадание произойдет при третьем выстреле.

Решение. По условию, р==0.6, q=0,4. k=3. Искомая вероят­ность по формуле (*.)

1. Понятие и вероятностный смысл математического ожидания дискретной случайной величины

Как уже известно, закон распределения пол­ностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничи­ваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины. К числу важных числовых характеристик относится математическое ожи­дание.

Математическое ожидание, как будет показано далее, приближенно равно среднему значению случайной вели­чины. Для решения многих задач достаточно знать мате­матическое ожидание. Например, если известно, что мате­матическое ожидание числа выбиваемых очков у первого стрелка больше, чем у второго, то первый стрелок в сред­нем выбивает больше очков, чем второй, и, следова­тельно, стреляет лучше второго. Хотя математическое ожидание дает о случайной величине значительно меньше сведений, чем закон ее распределения, но для решения задач, подобных приведенной и многих других, знание математического ожидания оказывается достаточным.

Математическое ожидание дискретной случайной величины

Математическим ожиданием дискретной слу­чайной величины называют сумму произведений всех ее возможных значений на их вероятности.

Если дискретная случайная величина Х принимает счетное множество возможных значений, то

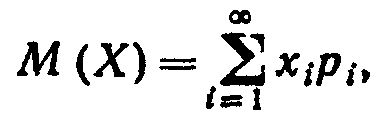
причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.

Замечание. Из определения следует, что математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина. Рекомендуется запомнить это утверждение, так как далее оно используется многократно. В дальнейшем будет пока­зано, что математическое ожидание непрерывной случайной величины также есть постоянная величина.

Пример 1. Найти математическое ожидание случайной вели­чины X. зная закон ее распределения:

Решение. Искомое математическое ожидание равно сумме произведений всех возможных значений случайной величины на их вероятности:

М (Х}==3.0,1 +5.0,6+2.0,3==3,9.

Пример 2. Найти математическое ожидание числа появлений события А в одном испытании, если вероятность события А равна р.

Решение. Случайная величина Х—число появлений события

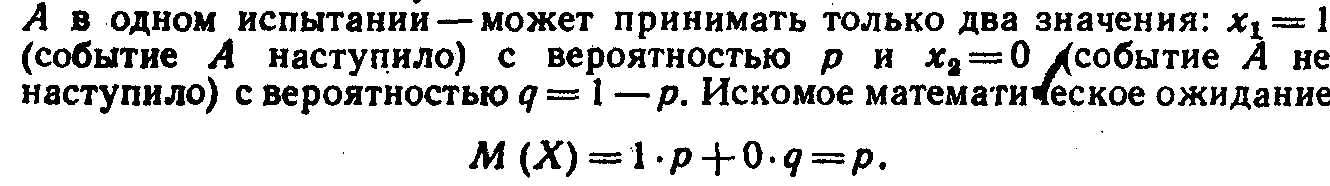
Итак, математическое ожидание числа появлений собы­тия в одном испытании равно вероятности этого собы­тия. Этот результат будет использован далее (ниже).