
- •Предмет теории вероятностей
- •2. Понятие события. Виды событий.
- •Виды случайных событий
- •3. Классическое и статистическое определение вероятности. Основные формулы комбинаторики
- •3.1 Классическое определение вероятности.Свойства вероятности.
- •3.2 Относительная частота. Устойчивость относительной частоты
- •3.3 Ограниченность классического определения вероятности. Статистическая вероятность.
- •3.4 Основные формулы комбинаторики
- •Решение. Искомое число способов
- •1. Понятие суммы и произведения событий.
- •2. Теоремы сложения вероятностей несовместных событий и событий, образующих полную группу событий
- •Теорема сложения вероятностей несовместных событий
- •2.2. Полная группа событий
- •Теорема сложения вероятностей противоположных событий. Принцип практической невозможности маловероятных событий.
- •3.1 Противоположные события
- •3.2. Принцип практической невозможности маловероятных событий
- •2. Теоремы умножения для зависимых и независимых событий.
- •Теорема о вероятности появления хотя бы одного независимого
- •Теорема сложения вероятностей совместных событий
- •2. Формула полной вероятности
- •Деталь может быть извлечена , либо из первого набора (событие в1), либо из второго (событие в2).
- •3. Вероятность гипотез. Формулы Бейеса
- •1) Деталь проверил первый контролер (гипотеза в1);
- •2) Деталь проверил второй контролер (гипотеза b2).
- •1. Формула Бернулли
- •2. Локальная теорема Лапласа
- •3. Интегральная теорема Лапласа
- •Случайная величина
- •Дискретные и непрерывные случайные величины
- •2. Закон распределения вероятностей дискретной случайной величины .
- •3. Биномиальный закон распределения .
- •4 . Распределение Пуассона
- •5 . Геометрическое распределение .
- •Понятие и вероятностный смысл математического ожидания дискретной случайной величины
- •Вероятностный смысл математического ожидания Пусть произведено «n» испытаний, в которых слу-
- •2. Свойства математического ожидания
- •Математическое ожидание случайной величины сх:
- •3. Теорема о математическом ожидании биномиального закона распределения
- •Дисперсия дискретной случайной величины и формула для ее вычисления.
- •1.1 Целесообразность введения числовой характеристики рассеяния случайной величины
- •1.2 Отклонение случайной величины от ее математического ожидания
- •1.3 Дисперсия дискретной случайной величины
- •1.4. Формула для вычисления дисперсии
- •2. Свойства дисперсии и их следствия.
- •Доказательство. По формуле для вычисления дисперсии имеем
- •Дисперсия числа появлений события в независимых испытаниях (дисперсия биномиального закона распределения)
- •3. Среднеквадратическое отклонение одной и суммы независимых случайных величин.
- •Среднее квадратическое отклонение суммы взаимно независимых случайных величин
- •4. Сущность и значение для практики теоремы Чебышева.
- •2. Свойства функции распределения
- •3. График функции распределения
- •1. Определение и свойства плотности распределения.
- •Свойства плотности распределения
- •2. Взаимосвязь функции и плотности распределения вероятностей.
- •Вероятностный смысл плотности распределения.
- •Вероятность попадания непрерывной случайной величины в заданный интервал
2. Свойства функции распределения
Свойство 1. Значения функции распределения принадлежат отрезку [a, b]:
![]()
Доказательство. Свойство вытекает из определения функции распределения как вероятности: вероятность всегда есть неотрицательное число, не превышающее единицы.
Свойство 2. F (х) —неубывающая функция, т. е.
![]()
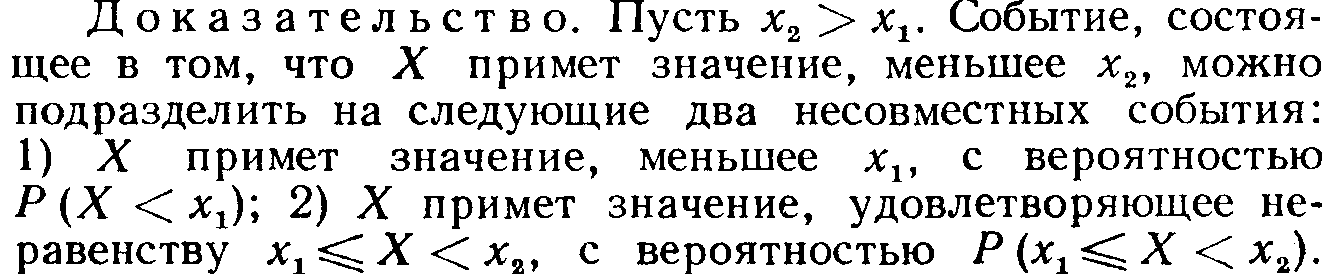
![]()
Отсюда
![]()
или
![]()
Так как любая вероятность есть число неотрицатель-
![]()
бовалось доказать.
Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (а, b), равна приращению функции распределения на этом интервале:
![]()
Это важное следствие вытекает из формулы (*), если
![]()
Пример. Случайная величина Х задана функцией распределения
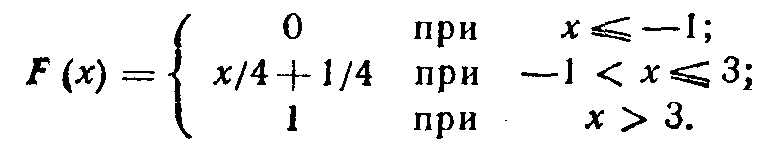
Найти вероятность того, что в результате испытания Х примет значение. принадлежащее интервалу (0. 2):
![]()
Решение. Так как на интервале (0, 2), по условию,
![]()
то
![]()
Итак,
![]()
Следствие 2. Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.
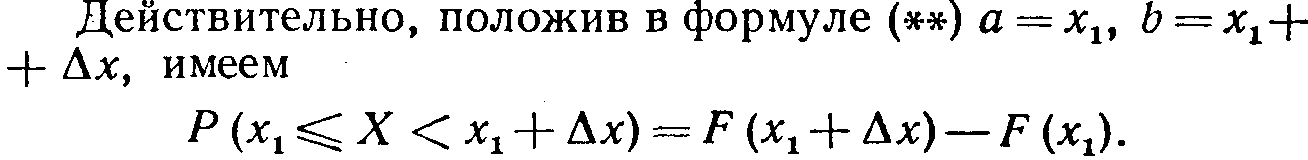
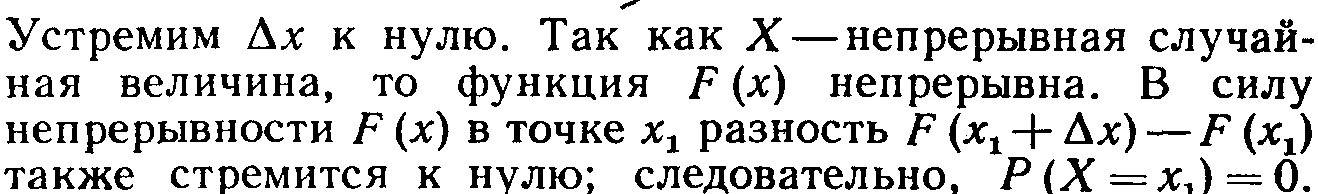
Используя это положение, легко убедиться в справедливости равенств
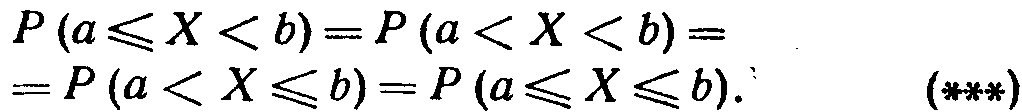
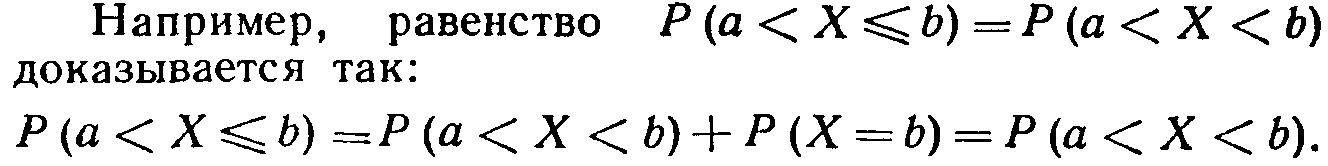
Таким образом, не представляет интереса говорить о вероятности того, что непрерывная случайная величина примет одно определенное значение, но имеет смысл рассматривать вероятность попадания ее в интервал, пусть даже сколь угодно малый. Этот факт полностью соответствует требованиям практических задач. Например, интересуются вероятностью того, что размеры деталей не выходят за дозволенные границы, но не ставят вопроса о вероятности их совпадения с проектным размером.
Заметим, что было бы неправильным думать, что ра-
![]()
классическим определением вероятности). Действительно, в результате испытания случайная величина обязательно примет одно из возможных значений; в частности, это

довательно, вероятность его равна единице.
Следствие. Если возможные значения непрерывной случайной величины расположены на всей оси х, то справедливы следующие предельные соотношения:
![]()
3. График функции распределения
Доказанные свойства позволяют представить, как выглядит график функции распределения непрерывной случайной величины.
График расположен в полосе, ограниченной прямыми у==0, у=1 (первое свойство).
При возрастании x в интервале (a, b), в котором заключены все возможные значения случайной величины, график «подымается вверх» (второе свойство).
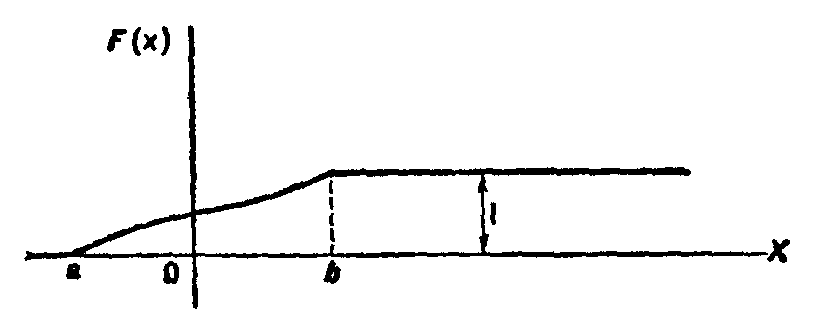
Рис. 1
При
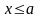 ординаты
графика равны нулю;
при
ординаты
графика равны нулю;
при

ординаты графика равны единице (третье свойство).
График функции распределения непрерывной случайной величины изображен на рис 1.
Замечание. График функции распределения дискретной случайной величины имеет ступенчатый вид.
Убедимся в этом на примере.
Пример. Дискретная случайная величина Х задана таблицей распределения
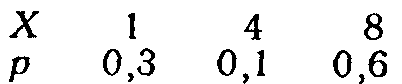
Найти функцию распределения и вычертить ее график.
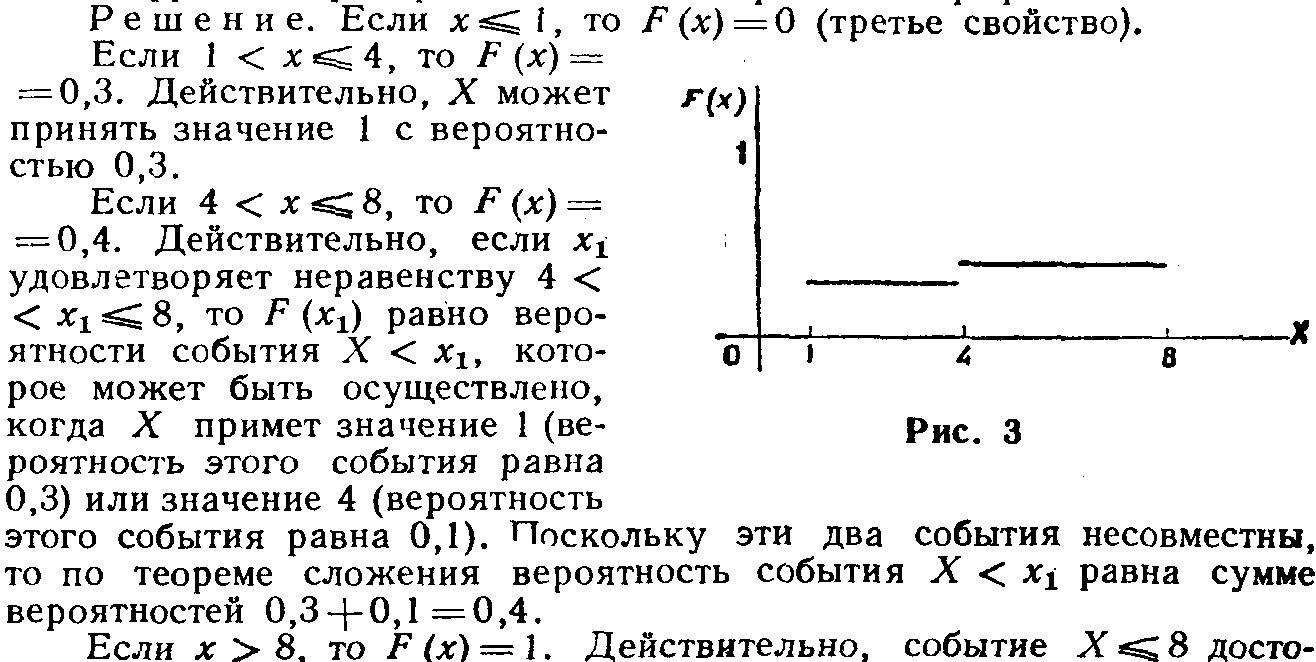
верно, следовательно, его вероятность равна единице.
Итак, функция распределения аналитически может быть записана так:
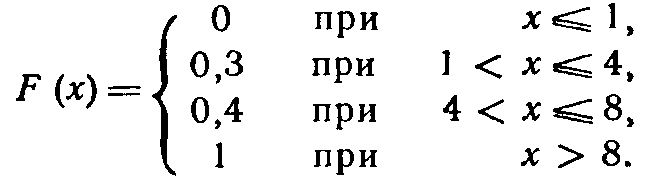
График этой функции приведен на рис. 3.
