Доказательство. По формуле для вычисления дисперсии имеем

Раскрыв скобки и пользуясь свойствами математиче­ского ожидания суммы нескольких величин и произведе­ния двух независимых случайных величин, получим

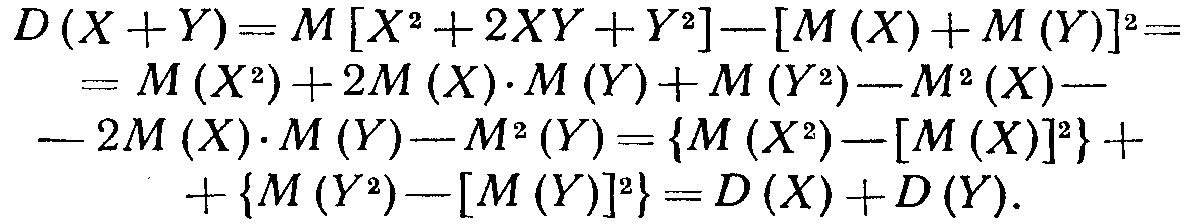
Итак,

Следствие 1.

Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин.

Например, для трех слагаемых имеем

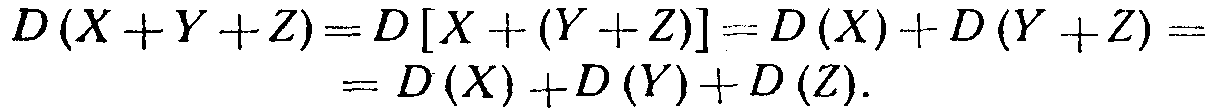
Для произвольного числа слагаемых доказательство проводится методом математической индукции.

Следствие 2.

Дисперсия суммы постоянной вели­чины и случайной равна дисперсии случайной величины:

Доказательство.

Величины С и Х независимы, поэтому, по третьему свойству,

В силу первого свойства D (С) == 0.

Следовательно,

Свойство становится понятным, если учесть, что ве­личины X и Х+С отличаются лишь началом отсчета и, значит, рассеяны вокруг своих математических ожиданий одинаково.

Свойство 4.

Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:

Доказательство.

В силу третьего свойства

По второму свойству,

или

Дисперсия числа появлений события в независимых испытаниях (дисперсия биномиального закона распределения)

Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А постоянна. Чему равна дисперсия числа появлений со­бытия в этих испытаниях? Ответ на этот вопрос дает следующая теорема.

Теорема. Дисперсия числа появлений события А в п не­зависимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления со­бытия в одном испытании:

3. Среднеквадратическое отклонение одной и суммы независимых случайных величин.

Для оценки рассеяния возможных значений слу­чайной величины вокруг ее среднего значения кроме дис­персии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение.

Средним квадратическим отклонением случайной ве­личины Х называют квадратный корень из дисперсии:

Легко показать, что дисперсия имеет размерность, равную квадрату размерности случайной величины. Так как среднее квадратическое отклонение равно квадратному

с размерностью X. Поэтому в тех случаях, когда жела­тельно, чтобы оценка рассеяния имела размерность слу­чайной величины, вычисляют среднее квадратическое от­клонение, а не дисперсию. Например, если Х выражается

Пример. Случайная величина Х задана законом распределения

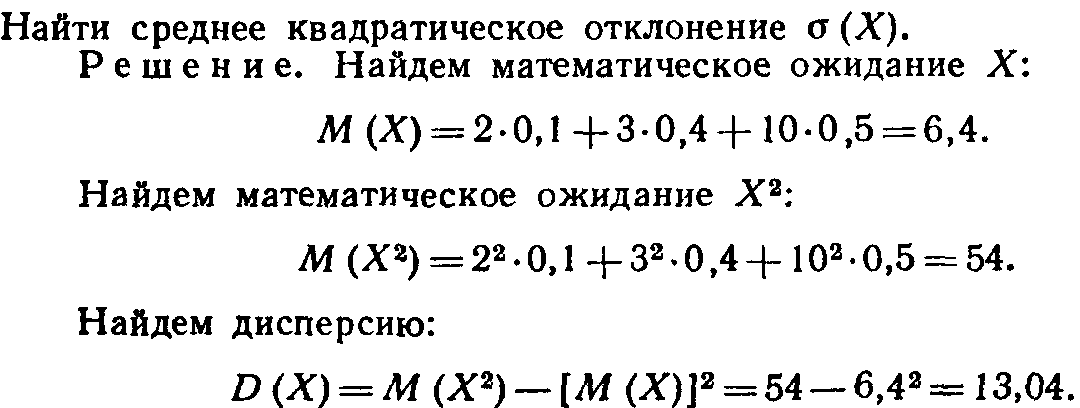
Искомое среднее квадратическое отклонение

Среднее квадратическое отклонение суммы взаимно независимых случайных величин

Пусть известны средние квадратические откло­нения нескольких взаимно независимых случайных вели­чин. Как найти среднее квадратическое отклонение суммы этих величин? Ответ на этот вопрос дает следующая теорема.

Теорема.

Среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин:

Доказательство. Обозначим через Х сумму рас­сматриваемых взаимно независимых величин:

Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий слагаемых поэтому

Отсюда

или окончательно