7.3. Истечение жидкости через насадки

В том случае, если стенка, через отверстие в которой происходит истечение, имеет значительную толщину по сравнению с размерами отверстия, то характер истечения существенным образом меняется, поскольку стенка влияет на направление струи. Аналогичный эффект наблюдается, если к отверстию в тонкой стенке присоединить короткую трубку того же диаметра, что и отверстие. Такие трубки длиной не менее 2,5-3 диаметров отверстия называются насадками или соплами. Присоединение насадка к отверстию изменяет расход вытекающей жидкости, и следовательно, изменяет время опорожнения сосуда.

Рассмотрим наружный цилиндрический насадок (рис. 7.5). Струя жидкости при входе в насадок сжимается, затем расширяется и заполняет все его сечение. В промежутке между сжатым сечением и стенками насадка образуется вихревая зона. Так как струя выходит из насадка полным сечением, то коэффициент сжатия струи =1, а коэффициент расхода , т.е. для насадка коэффициент расхода и коэффициент скорости имеют одинаковую величину.

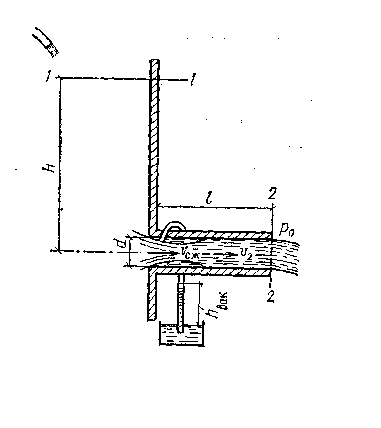
Рис. 7.5

Составим уравнение Бернулли для сечения 1-1 и 2-2, показанных на рис.7.5.

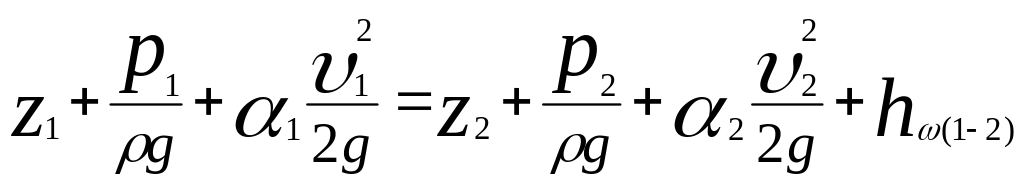
Принимая и что

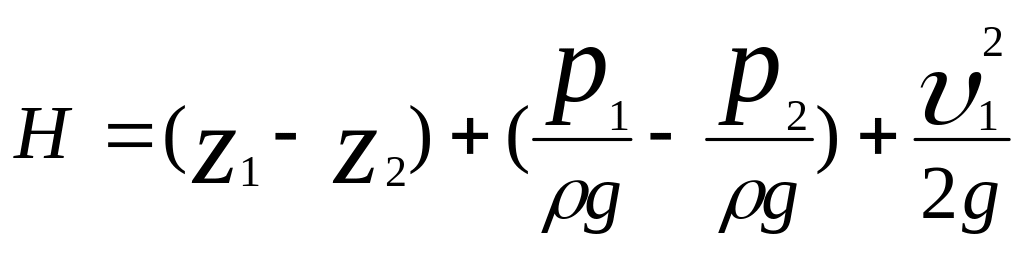, (7.24)

преобразуем уравнение к следующему виду

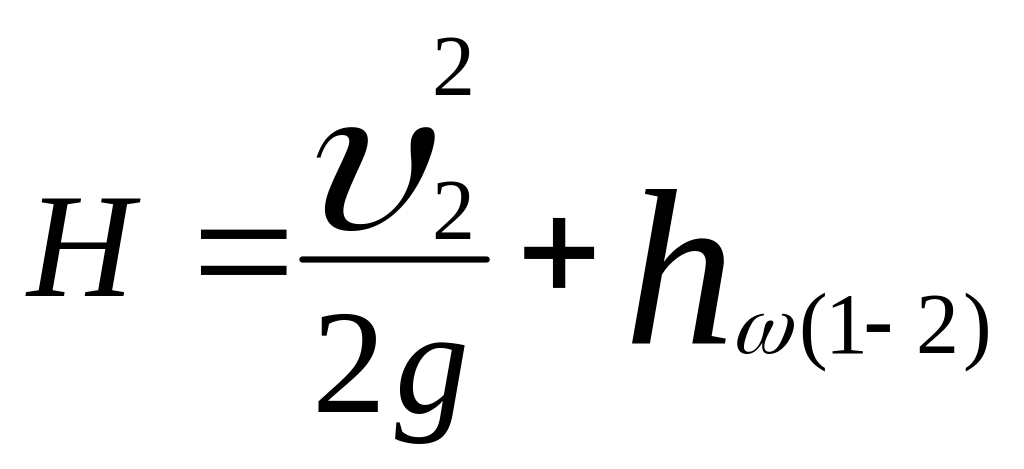. (7.25)

Потери напора в насадке складываются из потерь на вход в насадок и на внезапное расширение сжатой струи внутри насадка, т.е.

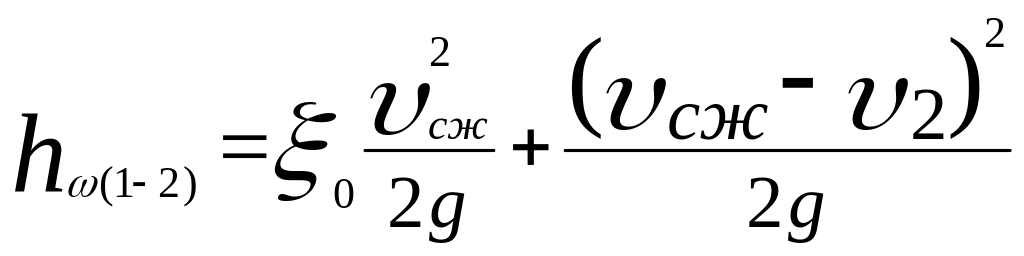. (7.26)

Из уравнения неразрывности имеем

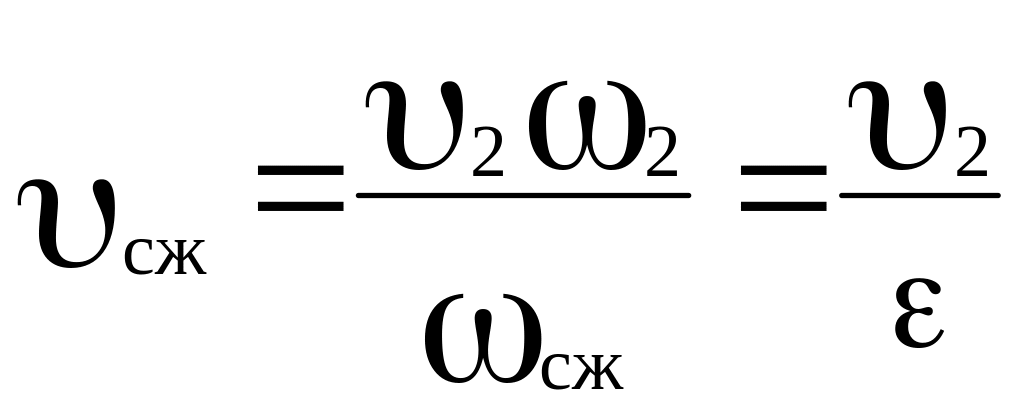. (7.27)

Подставляя выражение (7.27) а формулу (7.26), получим

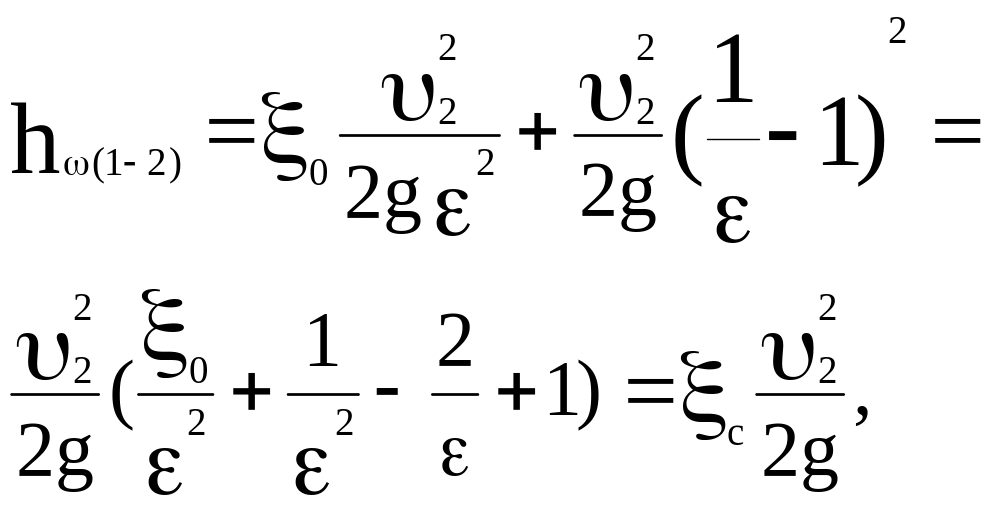(7.28)

где - коэффициент сопротивления сопла.

Уравнение (7.25) с учетом (7.28) запишется в виде

а скорость истечения из насадка

(2.29)

где введено обозначение

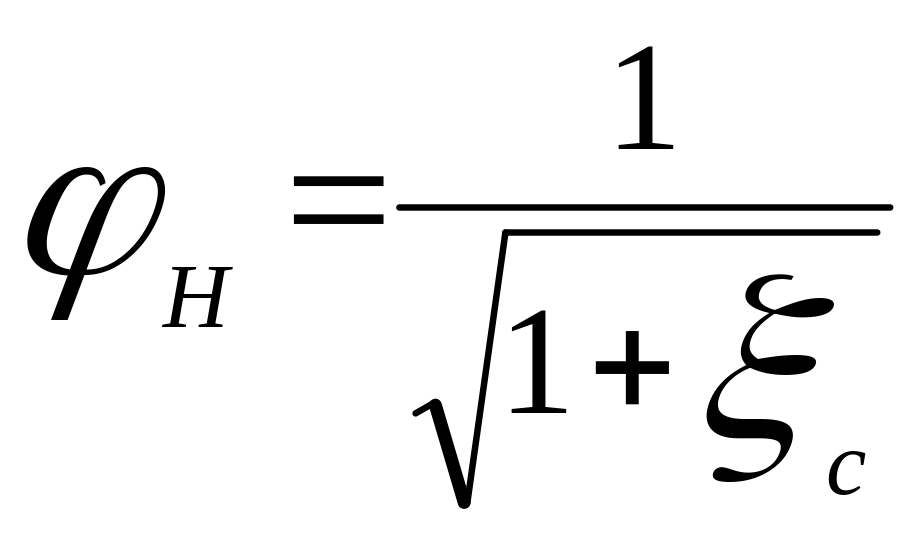. (7.30)

Для расхода получим формулу

.

Сравнивая ее со стандартной формулой , приходим к заключению, что

. (7.31)

Таким образом формулы скорости и расхода для насадка имеют тот же вид, что и для отверстия в тонкой стенке, но значения коэффициентов будут другими.

При истечении с большими числами Re ( =0), получаем следующее значение коэффициента расхода

0,845 . (7.32)

При истечении воды и воздуха в обычных условиях опыт показывает, что

0,82. (7.33)

Сравнивая коэффициенты расхода и скорости для насадка и отверстия в тонкой стенке, видим, что насадок увеличивает расход (более чем на 35%) и уменьшает скорость истечения примерно на 15%.

Действительно, для больших значений Re отношение 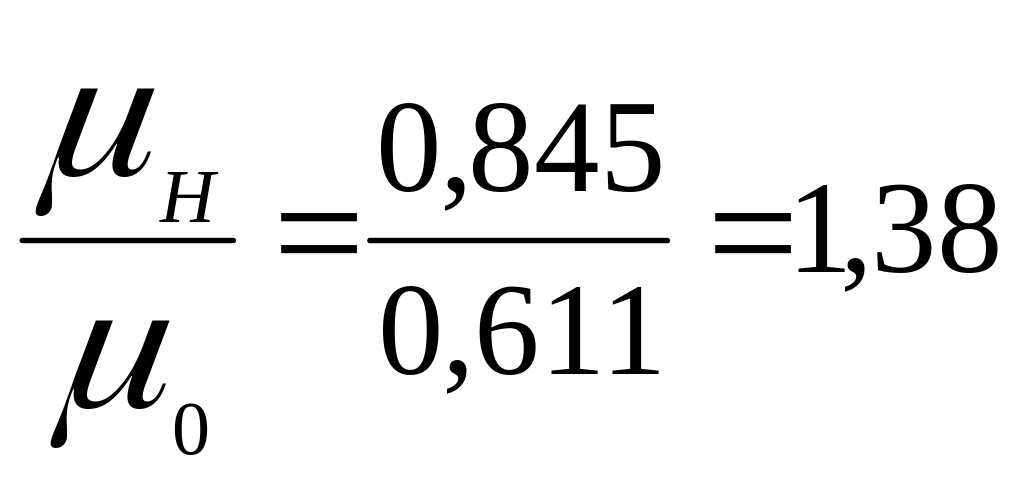и .

Для насадка характерно, что давление в сжатом сечении внутри насадка меньше атмосферного. Для определения величины вакуума в сжатом сечении насадка запишем уравнение Бернулли, связывающее это сечение с выходным сечением

, (7.34)

где 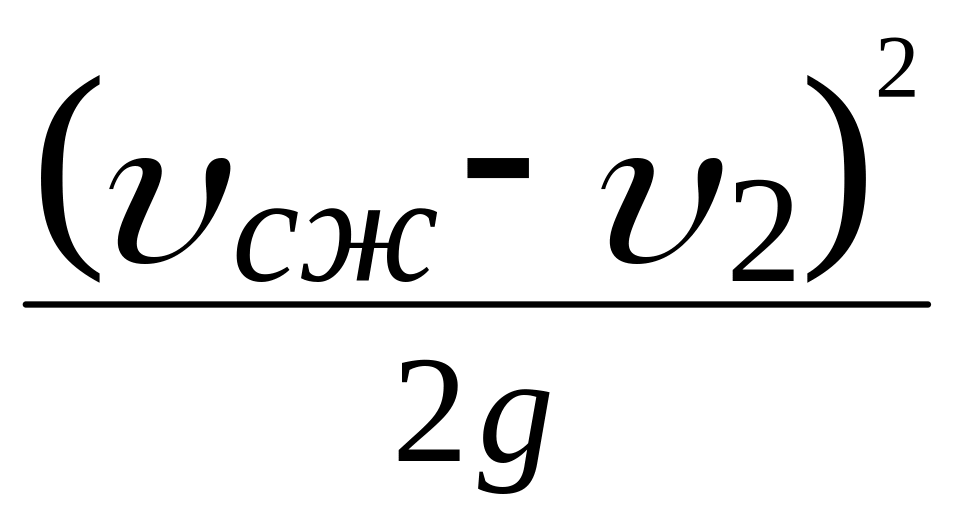- потери напора на внезапное расширение струи.

Далее получаем

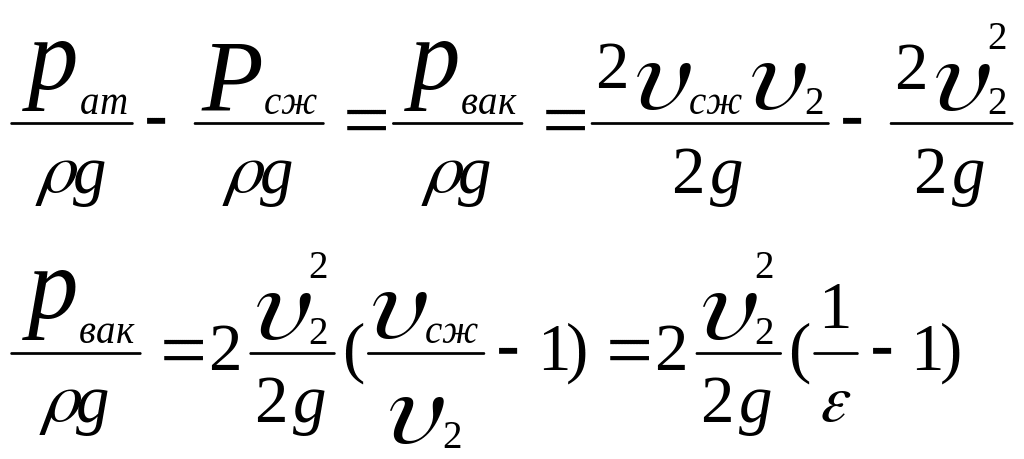
Принимая во внимание, что

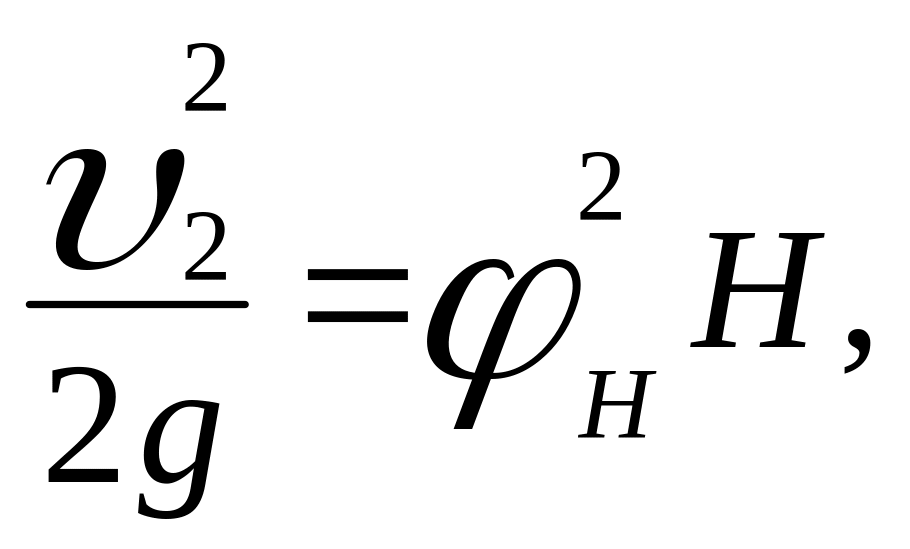
имеем

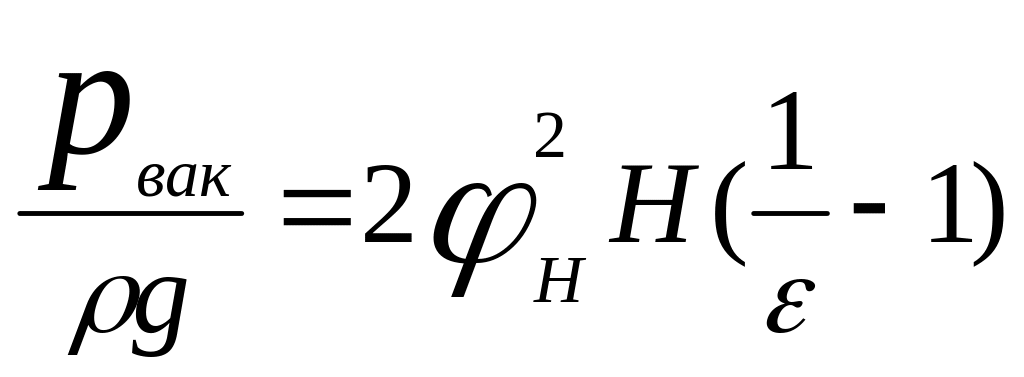
или 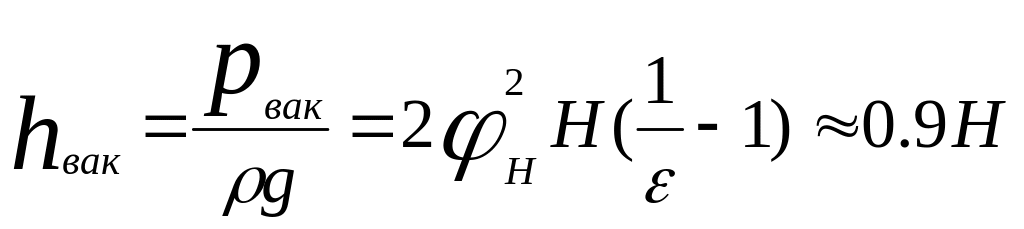. (7.35)

При истечении воды обычно принимают 0,75Н. В соответствии с уравнением (7.35) вакуум зависит от напора, возрастая с его увеличением. Предельное значение величины составляет 10,33м вод. столба, это соответствует предельной величине напора Н_пр=11,6м. При увеличении напора сверх Н_пр происходит отрыв струи от стенок и насадок начинает работать как отверстие в тонкой стенке (вакуум исчезает).