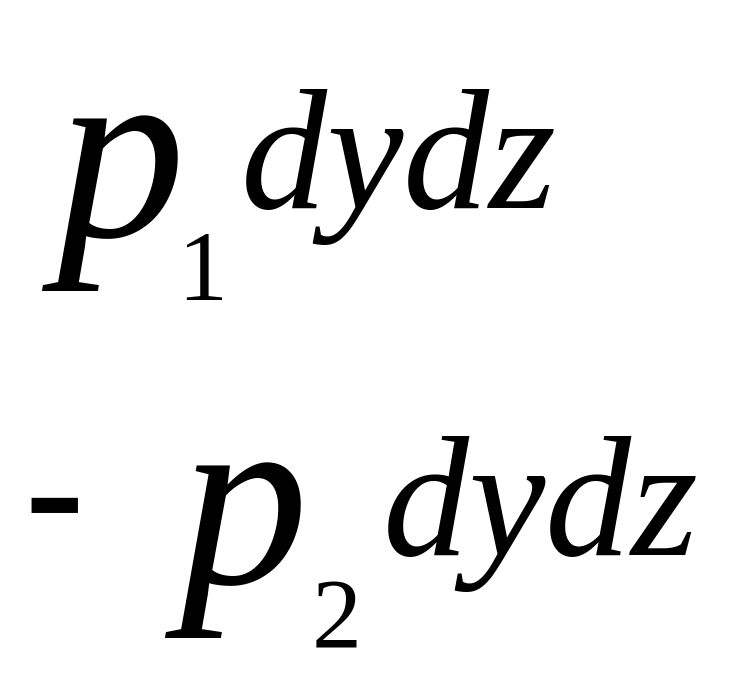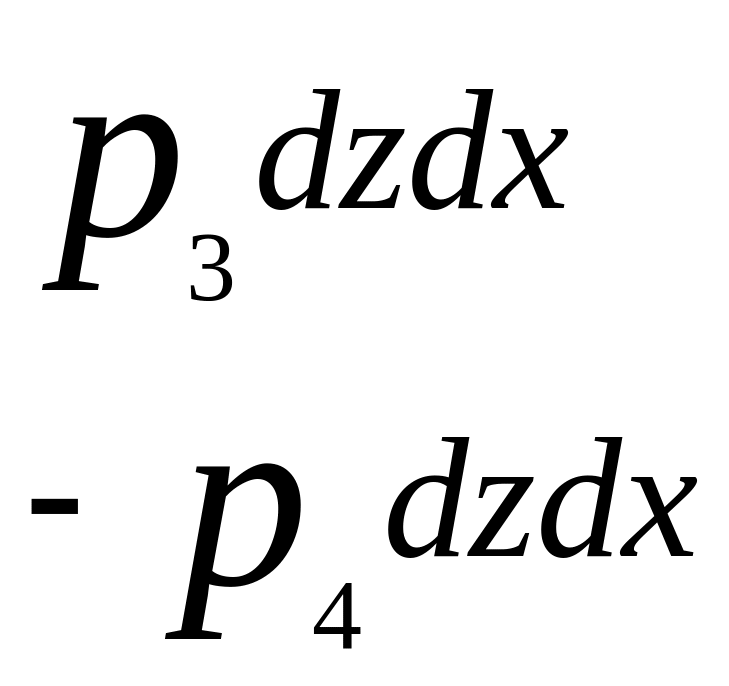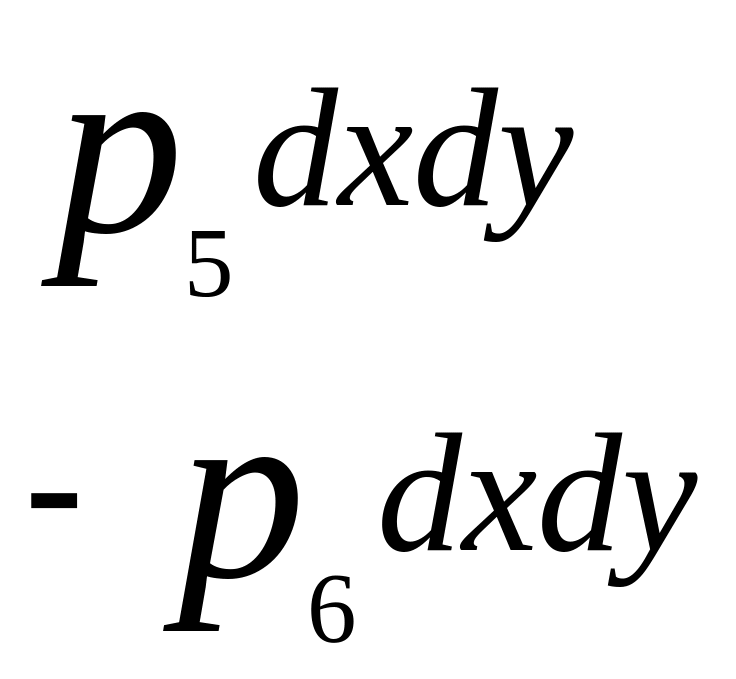- •2,Основные физические свойства жидкостей
- •1.1. Модели жидкостей
- •1.2. Основные физические свойства жидкости.
- •2. Гидростатика
- •2.1.Силы, действующие на жидкость. Давление в жидкости
- •2.2.Гидростатическое давление и его свойство
- •Дифференциальные уравнения равновесия жидкости
- •2.4 Равновесие жидкости в поле силы тяжести. Поверхность уровня
- •2.5 Относительное равновесие.
- •2.5.1. Движение резервуара с жидкостью по вертикали с постоянным ускорением а (рис.2.6).
- •2.6.Давление жидкости на твердые поверхности. Закон Архимеда
- •2.6.1.Давление жидкости на плоскую стенку
- •2.6.2.Давление жидкости на криволинейные поверхности. Закон Архимеда.
- •3.Кинематика жидкости и газа.
- •3.2.Уравнение неразрывности сжимаемой жидкости.
- •3.3. Движение жидкой частицы
- •4.Динамика жидкости
- •4.1. Уравнение Бернулли для элементарной струйки идеальной жидкости
- •Уравнение Бернулли для элементарной струйки вязкой жидкости
- •4.2. Основные дифференциальные уравнения движения идеальной жидкости в форме Эйлера и их интегрирование
- •Интегрирование уравнений Эйлера для установившегося движения.
- •4.3. Уравнение Бернулли для потока жидкости с поперечным сечением конечных размеров.
- •4.4. Уравнение движения вязкой жидкости (Уравнение Навье – Стокса)
- •5. Гидравлические сопротивления
- •5.1. Виды гидравлических сопротивлений
- •5.2. Режимы течения жидкости в трубах. Число Рейнольдса
- •5.3. Ламинарное течение в трубах. Одномерное течение
- •5.4. Турбулентное течение
- •5.5. Местные гидравлические сопротивления
- •5.5.1. Внезапное расширение трубопровода
- •5.5.2. Постепенное расширение трубопровода
- •5.5.3. Внезапное сужение трубопровода
- •5.5.4. Постепенное сужение трубы
- •6. Гидравлический расчет трубопроводов
- •6.1. Общие сведения. Простой трубопровод постоянного сечения
- •6.1.2. Расчет длинных трубопроводов в квадратичной области сопротивления.
- •6.2. Расчет сложных трубопроводов
- •6.2.1. Параллельное соединение трубопроводов
- •6.2.2. Непрерывная раздача расхода по пути (дырчатые трубопроводы)
- •6.2.3. Простая разветвленная сеть
- •6.2.4. Кольцевой трубопровод
- •7. Истечение жидкости через отверстия и насадки
- •7.1.Истечение жидкости из отверстий в тонкой стенке
- •7.1.1. В случае истечения из сосудов со свободной поверхностью
- •7.2. Истечение жидкости при переменном уровне
- •7.3. Истечение жидкости через насадки
- •8. Гидравлический удар
Уравнение Бернулли для элементарной струйки вязкой жидкости
Вязкая жидкость испытывает сопротивление при своем движении, и ее удельная энергия не может сохраняться неизменной вдоль струйки.
В соответствии с этим при движении
вязкой жидкости в уравнение Бернулли
необходимо внести поправку на потери
напора
![]() при переходе от одного сечения струйки
к другому, расположенному ниже по
течению
при переходе от одного сечения струйки
к другому, расположенному ниже по
течению
 (4.7)
(4.7)
или
![]() .
(4.8)
.
(4.8)
Линия, проведенная через концы отрезков Е, называется в этом случае линией полного напора. Она не является горизонтальной, ее значение уменьшается в направлении течения, и чем больше наклон этой линии, тем интенсивнее расходуется энергия по пути.
Отношение
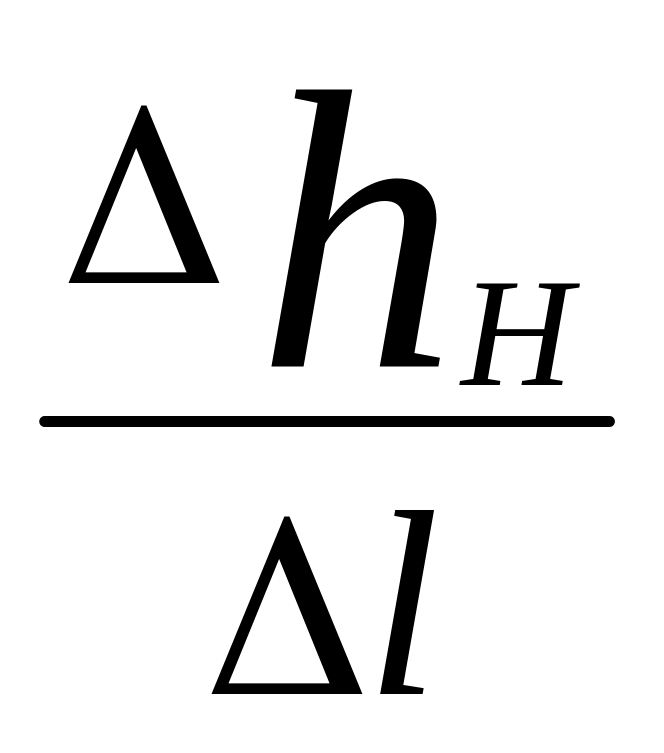 потерь на длине участка к самой длине
называют средним гидравлическим уклоном
для этого участка
потерь на длине участка к самой длине
называют средним гидравлическим уклоном
для этого участка
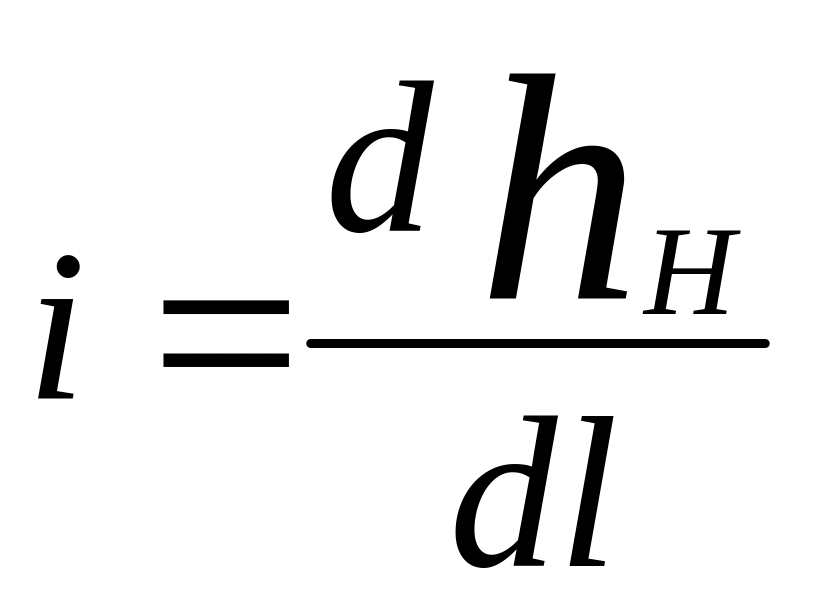 - уклон в данном сечении.
(4.9)
- уклон в данном сечении.
(4.9)
4.2. Основные дифференциальные уравнения движения идеальной жидкости в форме Эйлера и их интегрирование
 Выведем
дифференциальные уравнения для
произвольной идеальной сжимаемой
жидкости, движущейся относительно
прямоугольной системы координат OXYZ.
Из всей совокупности движущихся частиц
выделим в данный момент какую – нибудь
частицу жидкости в форме элементарного
прямоугольного параллелепипеда (рис.
4.3) со сторонами dx, dy,
dz.
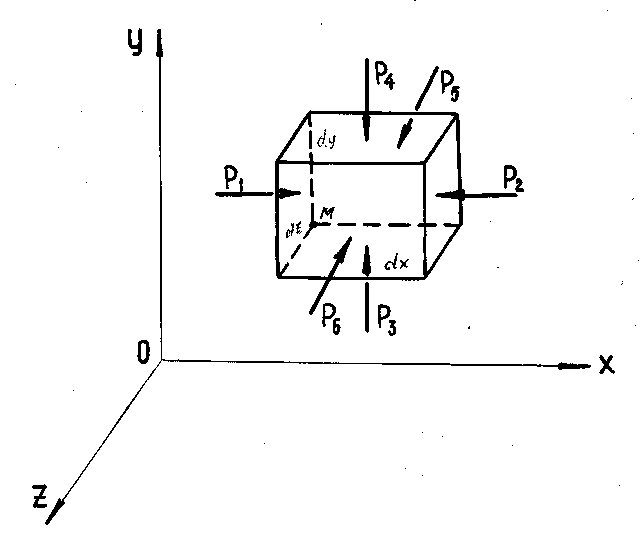
Выведем
дифференциальные уравнения для
произвольной идеальной сжимаемой
жидкости, движущейся относительно
прямоугольной системы координат OXYZ.
Из всей совокупности движущихся частиц
выделим в данный момент какую – нибудь
частицу жидкости в форме элементарного
прямоугольного параллелепипеда (рис.
4.3) со сторонами dx, dy,
dz.
Рис. 4.3
Задачу получения динамических уравнений для движущейся жидкости будем решать, используя принцип Даламбера.
Считая, что в данный момент времени бесконечно малая жидкая частица как бы отвердела, остановим ее и рассмотрим условия равновесия этой остановленной частицы. Как известно условиями равновесия являются шесть уравнений равновесия – три уравнения для проекций сил на оси координат и три уравнения для проекций моментов. Чтобы составить эти уравнения, нужно рассмотреть, какие силы действуют на рассматриваемую частицу жидкости.
На грани будут действовать поверхностные силы р1;р2…р6, являющиеся результатом воздействия на частицу окружающей жидкости. Величина каждой из них определится, очевидно, произведением среднего гидродинамического давления р, действующего по соответствующей площадке, на ее площадь dS.
Помимо поверхностных сил, на частицу будут действовать массовые силы, распределенные по всему ее объему, т.е. воздействующие на каждую точку внутри частицы (силы тяжести).
Проекции массовых сил, отнесенных к единице массы частицы, обозначим через X, Y, Z. Тогда, чтобы получить проекции массовых сил, действующих на всю частицу, нужно величины X, Y, Z умножить на массу частицы, равную . Таким образом, проекции массовой силы могут быть написаны в виде
![]()
Установив силы, действующие на частицу, для получения уравнений равновесия нужно применить принцип Даламбера. Согласно этому принципу действующие на частицу поверхностные и массовые силы в каждый момент времени уравновешиваются силами инерции. Обозначим через Ux, Uy, Uz проекции скорости бесконечно малой частицы по координатным осям. Тогда проекции ускорения частицы могут быть написаны в виде
![]()
Известно, что сила инерции численно равна произведению массы на ускорение, но направлена обратно ускорению. Следовательно, для проекций инерционной силы будем иметь следующие выражения:
![]() .
.
Для удобства последующих выкладок составим таблицу проекций на координатные оси всех полученных выше сил.
Таблица 4.1
Силы в проекции на |
Поверхностные |
Массовые |
Инерционные |
Ось Х
Ось Y
Ось Z
|
|
|
|
Чтобы получить уравнения равновесия, нужно приравнять нулю сумму поверхностных, массовых и инерционных сил. Для этого просуммируем сначала первую строчку таблицы и приравняем сумму нулю, затем то же сделаем с другими. В результате будем иметь следующие три уравнения равновесия:
![]()
![]()
![]()
Далее следовало составить три уравнения для моментов относительно координатных осей. Но мы эти уравнения писать не будем по той причине, что в пределе частица стягивается в точку и все силы будут сходящимися, т.е. уравнения моментов тождественно обратятся в нуль.
Для преобразования полученных трех уравнений вычислим прежде всего разность р1-р2.
Так как давление в идеальной жидкости не зависит от направления, то следовательно, давление по трем взаимно ортогональным бесконечно малым площадкам, проходящим через одну и ту же точку, одинаково. Обозначим его через р.
Тогда, очевидно, р1=р3=р5=р.
Давление р2 на правую грань параллелепипеда, отстоящую от левой грани на расстоянии dx , равно
р2=р+![]() .
.
Следовательно, искомая разность
![]() .
.
Подставив найденное выражение для
![]() в первое уравнение ,
в первое уравнение ,
получим
![]() .
.
Это уравнение можно переписать иначе:
![]()
Два другие уравнения получаются аналогично. В результате будем иметь следующую систему дифференциальных уравнений:
![]() (4.10)
(4.10)
Полученные уравнения являются основными дифференциальными уравнениями движения идеальной жидкости в форме Эйлера. Члены этих уравнений представляют собой соответствующие ускорения, а смысл каждого из уравнений заключается в следующем: полное ускорение частицы вдоль координатной оси складывается из ускорения от массовых сил и ускорения от сил давления.
Учитывая, что
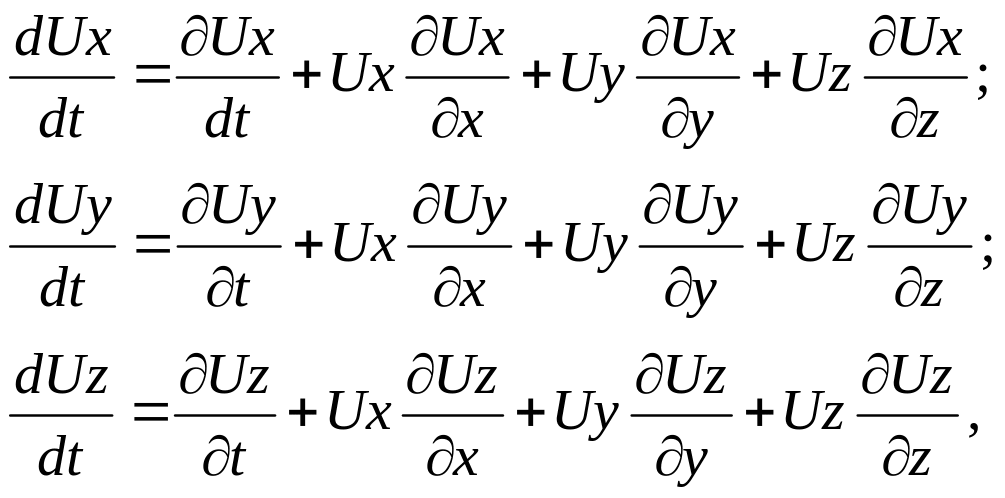
уравнения (4.10) можно записать в виде
![]() (4.11)
(4.11)
В систему трех уравнений входят пять неизвестных Ux, Uy, Uz, р и . Поэтому ее необходимо дополнить уравнениями неразрывности и состояния. Эти уравнения применимы как к несжимаемой жидкости, так и к сжимаемой, т.е. к газу. Различие будет только в характере изменения плотности . Если жидкость несжимаемая, то - величина постоянная; для газа будет величиной переменной.