5.5.2. Постепенное расширение трубопровода

Постепенно расширяющаяся труба называется диффузором. Течение жидкости в диффузоре сопровождается уменьшением скорости и увеличиваем давления, а следовательно, преобразованием кинетической энергии жидкости в энергию давления. Частицы движущейся жидкости преодолевают нарастающее давление за счет кинетической энергии, которая уменьшается вдоль диффузора и в направлении от оси к стенке.

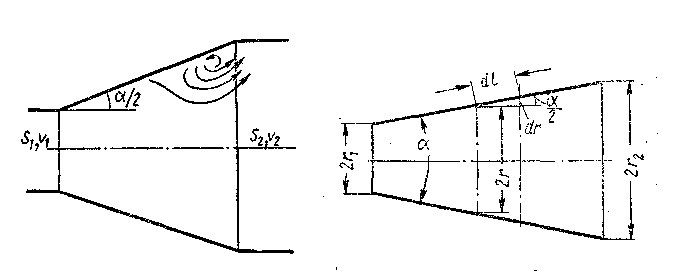Слои жидкости, прилегающие к стенкам, обладают столь малой кинетической энергией, что иногда оказываются не в состоянии преодолевать повышенное давление, они останавливаются или даже начинают двигаться обратно. Обратное движение (противоток) вызывает отрыв основного потока от стенки и вихреобразования (рис.5.10). Интенсивность этих явлений возрастает с увеличением угла расширения диффузора, а вместе с этим растут и потери на вихреобразование в нем.

Рис.5.10 Рис.5.11

Диффузор характеризуется двумя параметрами: углом конусности и степенью расширения n, определяемой отношением

.

Полную потерю напора в диффузоре условно рассматривают как сумму двух слагаемых:

, (5.21)

где и - потери напора на трение и расширение (вихреобразование).

Потерю напора на трение можно приближенно подсчитать следующим образом. Рассмотрим круглый диффузор с прямолинейной образующей и с углом при вершине. Пусть радиус входного отверстия равен r₁, выходного r₂ (рис. 5.11). Поскольку радиус сечения и скорости движения жидкости являются величинами переменными вдоль диффузора, то возьмем элементарный отрезок диффузора длиной вдоль образующей и для него выразим элементарную потерю напора на трение по основной формуле

,

где - средняя скорость в произвольно взятом сечении, радиус которого r.

Из элементарного треугольника следует:

.

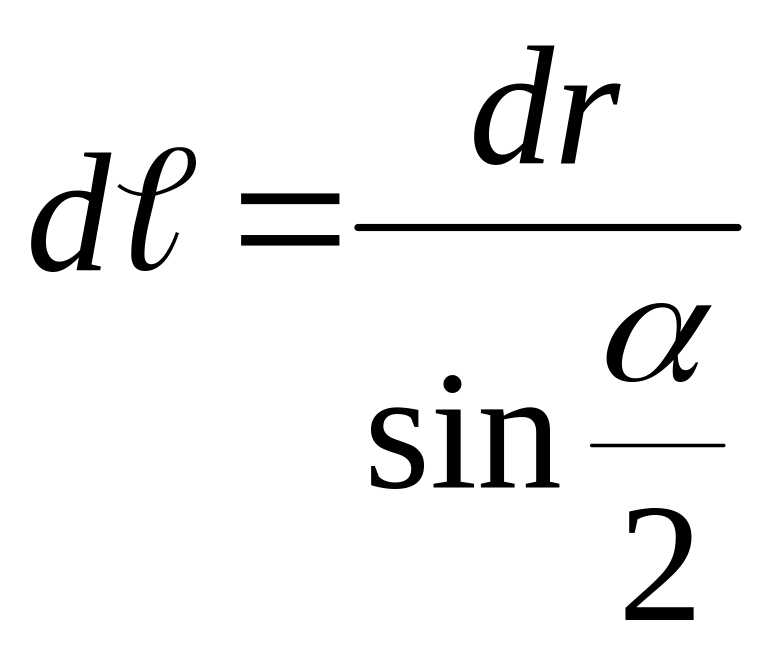Далее, на основании уравнения расхода можно записать

, ;

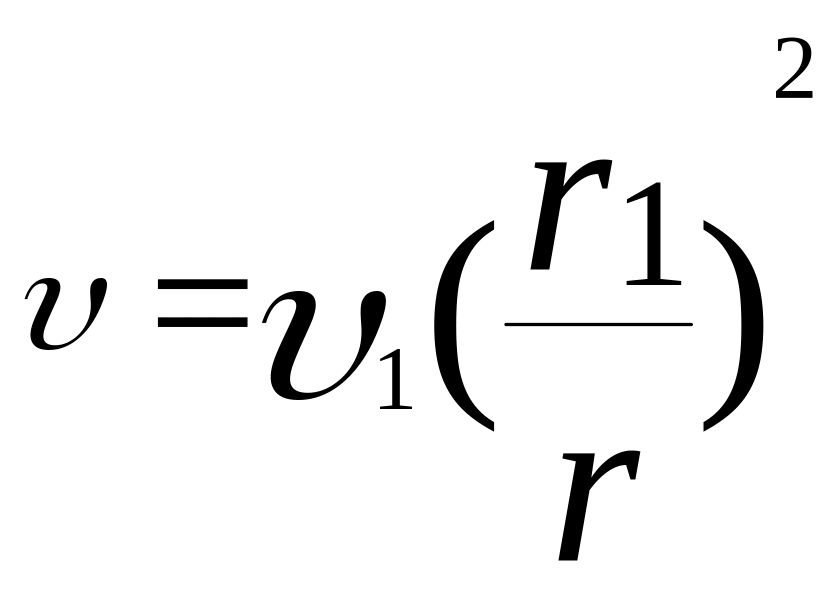где - скорость в начале диффузора.

Подставляя эти выражения в формулу для и выполняя интегрирование в пределах от r₁ до r₂, т.е. вдоль всего диффузора, считая при этом коэффициент постоянным, получим

,

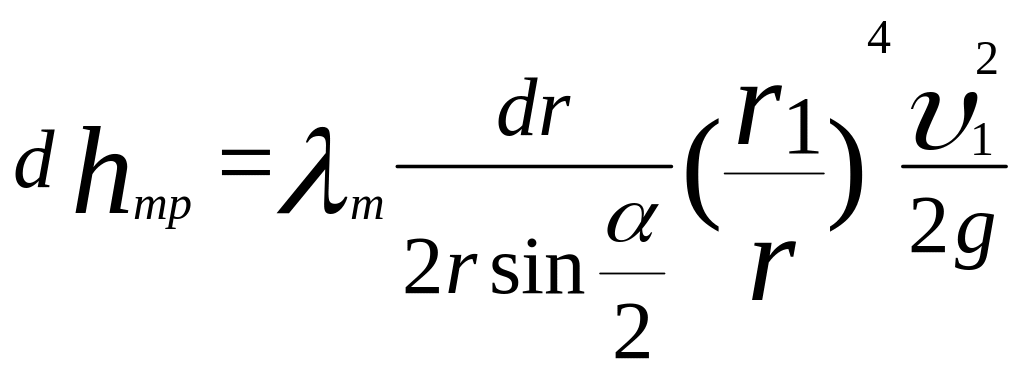откуда

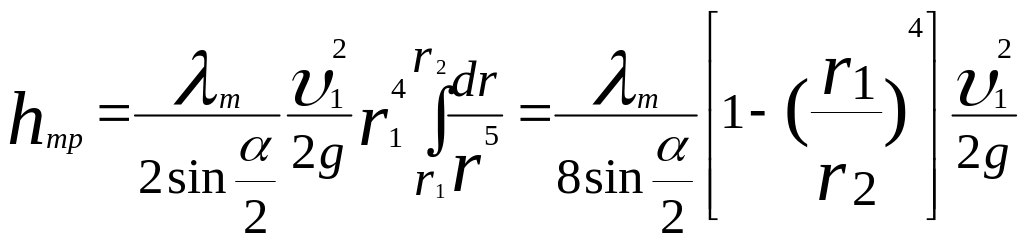
или

, (5.22) где 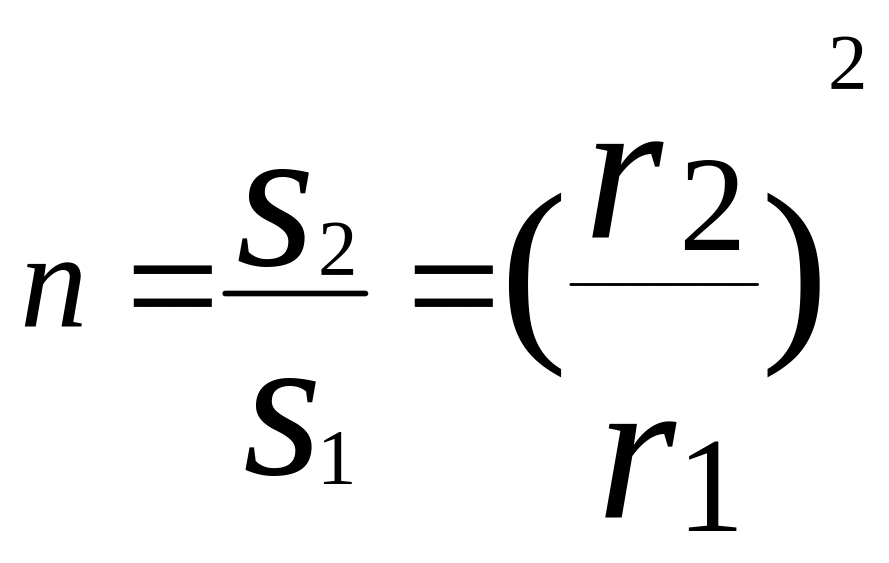- степень расширения диффузора.

Второе слагаемое – потеря напора на расширение имеет в диффузоре ту же природу, что и при внезапном расширении, но меньшее значение, поэтому оно обычно выражается по той же формуле (5.19) или (5.20), но с поправочным коэффициентом к, меньшим единицы,

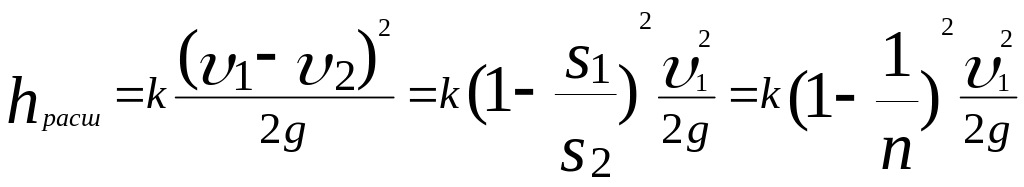. (5.23)

Так как в диффузоре по сравнению с внезапным расширением торможение потока как бы смягченное, коэффициент называют коэффициентом смягчения. Его численное значение для диффузоров с углами конусности =5-20⁰ можно определять по приближенной формуле

. (5.24)

Учитывая (5.22) и (5.23), уравнение (5.21) можно переписать в виде

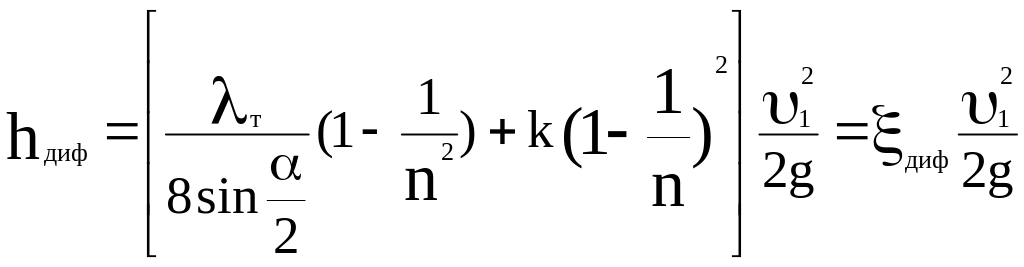, (5.25)

а коэффициент сопротивления диффузора можно выразить формулой

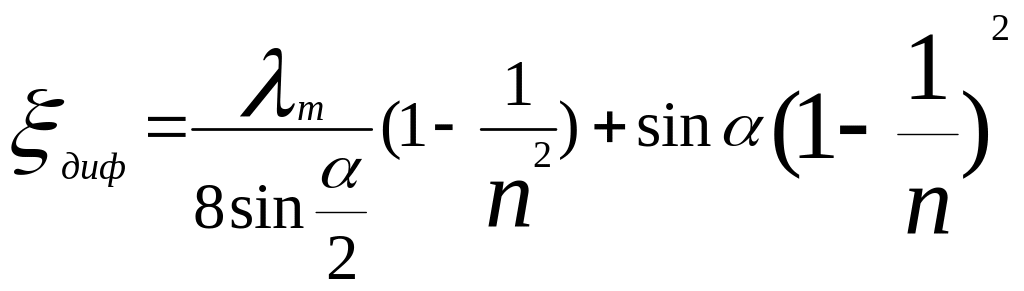. (5.26)

Последнее выражение показывает, что коэффициент зависит от угла , коэффициента и степени расширения n.

С , при заданных и n, первое слагаемое в формуле (5.26), обусловленное трением, , т.к. диффузор становится короче, а второе слагаемое, обусловленное вихреобразованием и отрывом потока, , и наоборот. Оптимальный угол конусности лежит в пределах от 5 до 8⁰.