21 «Істинне» рівняння регресії. Парна регресія. Систематична та випадкова складові.

Нехай маємо набір значень двох змінних – пояснювальна змінна та – пояснююча змінна, кожна з яких містить n спостережень. Нехай між ними теоретично існує деяка лінійна залежність

Це рівняння будемо називати «істинним» рівнянням регресії.

Враховуючи можливі відхилення лінійне рівняння зв’язку двох змінних (парну регресію) представимо у вигляді де – постійна величина (або вільний член рівняння); – коефіцієнт регресії, що визначає нахил лінії. вздовж якої розсіяні дані_спостереження; – випадкова змінна (випадкова

складова, залишок або збурення).

У векторно-матричній формі, співвідношення буде мати такий вигляд:

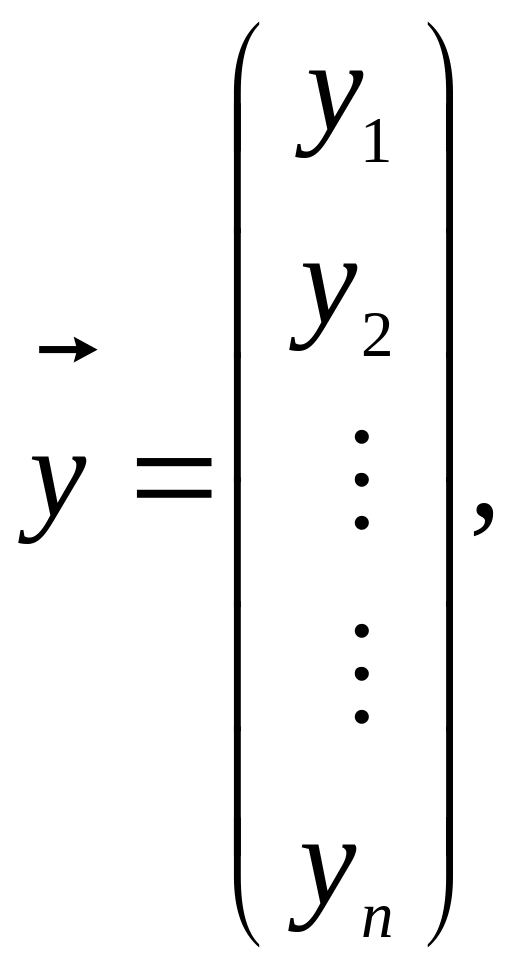
Випадкова складова відображає той факт, що зміна буденеточно описуватися зміною , оскільки присутні інші фактори, невраховані в даній моделі. Таким чином в рівнянні ,значеннякожного спостереження представлено як сума двох частин –систематичної та випадкової . В свою чергу систематичну частину можна представити у вигляді рівняння

22.Умови Гаусса-Маркова.

Для того, щоб регресійний аналіз, що базується на звичайному методі найменших квадратів (МНК) давав найкращі із всіх можливі результати, необхідно щоб виконувалися певні умови, які називаються умовами Гаусса-Маркова, а саме:

1.Математичне_сподівання випадкових відхилень повинно дорівнювати нулеві (незміщеність оцінок):

Умова вимагає, щоб випадкові відхилення в середньому не впливали на залежну змінну Y, тобто в кожному конкретному спостереженні відхилення може набувати додатні або від’ємні значення, але не повинно спостерігатися систематичне зміщення відхилень в переважній більшості в бік одного знаку.

Із_врахуванням вищесказаного, будемо мати:

2. Дисперсія випадкових відхилень повинна_бути_сталою_величиною ,

Ця вимога передбачає, що не зважаючи на те, що при кожному конкретному_спостереженні випадкове відхилення може виявитися відносно великим чи малим, це не повинно складати основу для апріорної причини, тобто причини, що не базується на досвіді, що спонукала б велику похибку. Моделі, для яких виконується ця умованазивають гомоскедастичними (рівнозмінними). Моделі, для яких не виконується умова називають гетероскедастичними.

3. Випадкові відхилення та , повинні бути незалежними одне від одного.

Виконання цієї умови припускає, що між будь-якими випадковими відхиленнями_відсутній систематичний зв’язок, тобто величина та знак будь-якого випадкового відхилення не буде являтися причиною величини та знаку будь-якого іншого випадкового відхилення. Цю умову можна записати так

(3.8)