15) Якісна оцінка коефіцієнтів кореляції за шкалою Чеддока. Розподіл Фішера-Іейтса.

Для якісної оцінки коефіцієнтів кореляції застосовуються різні шкали, найбільш часто – шкала Чеддока. В залежності від значень коефіцієнта кореляції зв'язок може мати одну з оцінок

0,1-0,3 – слабкий;

0,3-0,5 – помітний;

0,5-0,7 – помірний;

0,7-0,9 – високий;

0,9-1,0 – вельми високий.

Варто відмітити, що величина коефіцієнта кореляції не є доказом того, що між ознаками, що досліджуються, є причинно-наслідковий зв'язок, а являє собою оцінку ступеня взаємної узгодженості в змінах ознак. Для того, щоб встановити причинно-наслідкову залежність необхідним є аналіз якісної природи явищ.

Вибірковий коефіцієнт кореляції r застосовується в основному для перевірки загальної гіпотези про наявність кореляції між спостережуваними величинами, не вдаючись у детальні оцінки сили цієї кореляції.

Отже, для перевірки гіпотези про відсутність кореляції, необхідно перевіряти, значимо чи r відрізняється від нуля. А для цього потрібно знати розподіл r як випадкової величини. Цей розподіл відомий, але, як і варто було очікувати, воно залежить від невідомого генерального коефіцієнта . Однак, якщо ми як нульову візьмемо гіпотезу, що = 0 (відсутність кореляції), то r-розподіл відповідний = 0, сильно спрощується і буде залежати тільки від обсягу вибірки. Його щільність має вигляд

r-Розподіл називають розподілом Фішера-Іейтса. Видно, що це симетричний відносно нуля унімодальний розподіл. У статистичних таблицях наведені квантилі цього розподілу для деяких рівнів значимості та ступенів свободи.

У припущенні, що генеральна кореляція = 0, інтервальна оцінка для r з довірчою ймовірністю р = 1 - , очевидно, дорівнює

.

Отже, якщо виявиться, що знайдений за вибіркою коефіцієнт r задовольняє нерівності

то його потрібно визнати значущим, тобто потрібно вважати, що нульова гіпотеза невірна. А це означає, що   0 і між величинами, що спостерігаються, є кореляція. Вона буде тим сильніше, чим значніше | r | перевищує і наближається до 1.

16, 14(1)) Поняття кореляції. Оцінка значимості коефіцієнта кореляції з використанням t-критерію Стьюдента.

Оцінка значимості коефіцієнта корреляції при малих обсягах вибірки виконується з використанням t-критерію Стьюдента. При цьому фактичне (спостережне) значення цього критерію визначається за формулою

Розраховане за цією формулою значення порівнюється з критичним значенням t-критерію Стьюдента з урахуванням заданного рівня значущості та числа ступенів свободи n-2.

Якщо , то отримане значення коефіцієнта кореляції признається значущим і робиться висновок про тісний статистичний взаємозв’язок величин.

17) Матриця коефіцієнтів парної кореляції. Вибірковий коефіцієнт множинної кореляції та коефіцієнт детермінації. Вибірковий частинний коефіцієнт кореляції.

Матриця коефіцієнтів парної кореляції

Коефіцієнти парної кореляції використовуються для виміру сили лінійних зв’язків різних пар ознак з їх множини. Для множини ознак отримують матрицю коефіцієнтів парної кореляції.

Нехай вся сукупність даних складається зі змінної _Y та m змінних (факторів) Х, кожна з яких містить n спостережень. Тоді можна розрахувати матрицю коефіцієнтів парної кореляції R, вона симетрична відносно гловної діагоналі

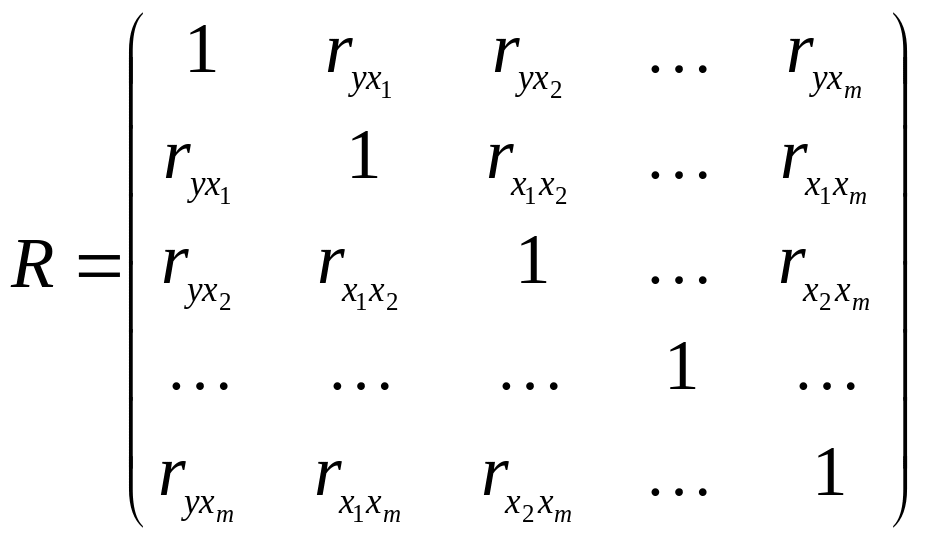
Аналіз матриці коефіцієнтів парної кореляції використовується при побудові моделей множинної регресії.

Однією кореляційною матрицею неможливо повністю описати залежності між величинами. У зв’язку з цим в багатомірному кореляційному аналізі розглядаються дві задачі:

1)визначення тісноти зв’язку однієї випадкової величини з сукупністю інших величин, що включені в дослідження;

2)визначення тісноти зв’язку між двома величинами при фіксуванні або виключенні впливу інших величин.

Ці задачі вирішуються відповідно за допомогою множинної чи частинної кореляції.

Вибірковий коефіцієнт множинної кореляції визначається за формулою

,

де  – визначник кореляційної матриці ;

– алгебраїчне доповнення елемента тієї ж матриці.

Квадрат коефіцієнта множинної кореляції прийнято називати вибірковим множинним коефіцієнтом детермінації. Він показує яку частку варіації (випадкового розкиду) досліджуємої величини пояснює варіація інших випадкових величин .

Перевірка значущості коефіцієнта детермінації здійснюється шляхом порівняння розрахункового значення F-критерію Фішера

,

з табличним . Табличне значення критерію визначається заданим рівнем значущості та числа ступенями свободи та (де p – кількість параметрів моделі). Коефіцієнт значимо відрізняється від нуля, якщо виконується нерівність

.

Якщо випадкові величини, що розглядаються, корелюють один з одним, то на величину парної кореляції частково мають вплив інші величини. У зв’язку з цим виникає необхідність дослідження частинної кореляції між величинами при виключенні впливу інших випадкових величин (однієї чи декількох).

Вибірковий частинний коефіцієнт кореляції визначається за формулою

,

де  – алгебраїчні доповнення до відповідних елементів матриці .

За умови, що m=3, вираз (2.16) буде мати вигляд

,

Коефіцієнт називається коефіцієнтом кореляції між та при фіксованому .