14) Поняття кореляція. Кореляційний момент або коваріація. Коефіцієнт кореляції. Вибірковий кореляційний момент. Стандартна похибка.
Кореляція. Вибірковий коефіцієнт кореляції
Між випадковими величинами може існувати лише стохастичний зв'язок, при якому із зміною однієї величини змінюється розподіл іншої. Виявлення стохастичного зв'язку та оцінка його сили – важлива і важка задача математичної статистики. Досить сказати, що це завдання в загальному вигляді не вирішено.
Відомо, що дисперсія суми двох незалежних величин дорівнює сумі дисперсій цих величин. Тому, якщо для двох випадкових величин X і Y виявиться, що
D(X + Y) D(X) + D(Y), (2.1)
то це слугує вірною ознакою наявності залежності між X и Y.
При виконанні вказаної нерівності будемо говорити, що випадкові величини X і Y корельовані і кореляція тим сильніше, чим більш відмінні дисперсії суми від суми дисперсій.
Встановимо величину кореляції між випадковими величинами X і Y. Безпосередньо з властивостей математичного сподівання і дисперсії випливає, що
де
Отже,
сила кореляції визначається величиною
яку з цієї причини називають кореляційним
моментом
або коваріацією.
Отже, коваріація – це статистична
міра взаємодії двох змінних. Очевидно,
необхідною і достатньою умовою кореляції
служить нерівність
Кореляційний момент залежить від одиниць
вимірювання величин X
і Y,
тому на практиці частіше використовується
безрозмірна величина
яка
називається коефіцієнтом кореляції.
Таким
чином, якщо випадкові величини X
і Y
залежні, то коефіцієнт кореляції
відмінний від нуля. На жаль, зворотне
твердження невірно: з рівності
не витікає незалежність випадкових
величин.
Запишемо очевидні рівності:
З визначення коефіцієнта кореляції випливає, що він не змінюється при переході від X і Y до нормованим величин:
для
яких
В цьому випадку з (2.5) отримуємо
(2.7)
звідки
витікає, що
тобто
Якщо
коефіцієнт кореляції відмінний від
нуля, то він своєю величиною характеризує
не тільки наявність, а й силу зв'язку
між змінними. Чим більше ||,
тим сильніше зв'язок (кореляція).
Максимальна кореляція значенням =
1. Як неважко помітити, в цьому випадку
або
,
отже,
або
Повертаючись до величин X і Y, відмічаємо,
що при
=
1 між ними існує строгий функціональний
(причому, лінійний) зв'язок.
Зі сказаного випливає, що при 0 < || <1 між Y і X може бути як стохастичний зв'язок, так і функціональний (нелінійний) без сліду випадковості. У цьому полягає серйозний недолік коефіцієнта кореляції. Ми можемо лише вважати, що є показником того, наскільки зв'язок між випадковими величинами Y і X близький до строгої лінійної залежності.
Незміщеними
оцінками кореляційного моменту
і дисперсій
і
є вибірковий
кореляційний момент
(вибіркова коваріація)
і вибіркові
дисперсії
і
.
Тоді якщо відомі
–
фактичні значення змінних X
і Y,
то вибіркова коваріація між ними
розраховується наступним чином
,)
де
–
середні арифметичні відповідних величин.
Видно, що у виразі для присутній один зв'язок (добуток середніх), тому для нього, як і для вибіркових дисперсій, число ступенів свободи дорівнює n-1.
Той факт, що для отримання незміщеної оцінки s2 в знаменнику вибіркової дисперсії довелося n замінити на n-1, безпосередньо пов'язаний з тим, що величина відносно якої беруться відхилення, сама залежить від елементів вибірки. Якщо б у формулі вибіркової дисперсії були дві такі величини, то n потрібно було б замінити на n-2 і т.д.
Кожна величина, яка залежить від елементів вибірки і є у формулі вибіркової дисперсії, називається зв'язком. Виявляється, що знаменник вибіркової дисперсії завжди дорівнює різниці між обсягом вибірки n і числом зв'язків, накладених на цю вибірку. Число r = n-l називається числом ступенів свободи.
Вибірковий коефіцієнт кореляції (коефіцієнт кореляції Пірсона) розраховується за формулою
.
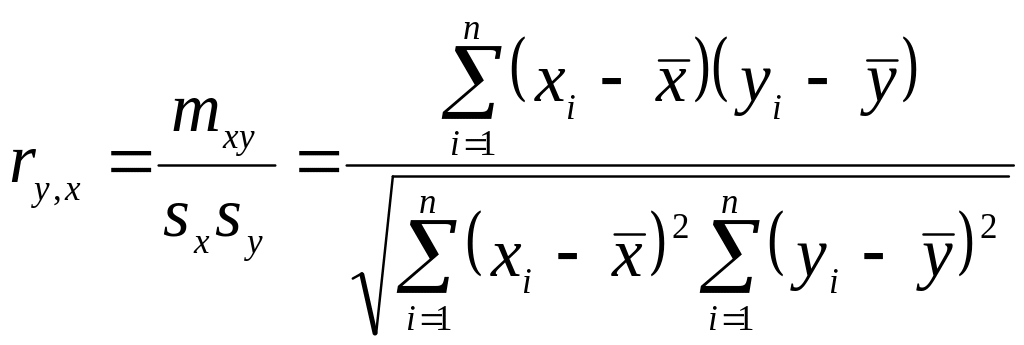При цьому оцінка дисперсії характеризує ступінь розкиду значень навколо їх середнього або варіабельність та визначається за формулою
В загальному випадку для отримання незміщеної оцінки дисперсії суму квадратів необхідно поділити на число ступенів свободи. Так як вибірка вже використовувалася один раз для визначення середнього Х, то число накладених зв’язків в даному випадку дорівнює одиниці, а число ступенів свободи n-1.
Однак, більш природно вимірювати ступінь розкиду значень змінних в тих же одиницях, в яких вимірюється і сама змінна. Цю задачу вирішує показник, що називається середньоквадратичним відхиленням (стандартним відхиленням) або стандартною похибкою і визначається співвідношенням
.