31 Нелінійна регресія відносно пояснюючих змінних. Нелінійна регресія по параметрам, що оцінюються. Внутрішньо лінійна та нелінійна функції.

При вивченні залежностей економічних показників на основі реальних статистичних даних з використанням апарату теорії ймовірностей та математичної статистики можна зробити висновки, що лінійні залежності зустрічаються не так часто. Їх використовують лише як частковий випадок для зручності та наочності розгляду економічного процесу. Частіше зустрічаються моделі,які відображають економічні процеси у вигляді нелінійної залежності. Існує також так звана кускова функція, яка на різних ділянках області визначення може бути задана різними аналітичними виразами.

Якщо між економічними явищами існують нелінійні відношення, то вони виражаються за допомогою відповідних нелінійних функцій.

Розрізняють два класи нелінійних регресій:

1)нелінійні відносно пояснюючих змінних, однак лінійні по параметрам, що оцінюються;

2)нелінійні по параметрам, що оцінюються.

Клас регресій нелінійних відносно пояснюючих змінних, однак лінійних по параметрам, що оцінюються, включає рівняння, в яких залежна змінна лінійно пов’язана з параметрами. Приклад таких регресій можуть слугувати:

-поліноми різних ступенів

; (5.1)

рівностороння гіпербола

. (5.2)

При оцінці параметрів регресії, нелінійних по пояснюючим змінним, використовується метод заміни змінних. Суть його полягає в заміні нелінійних пояснюючих змінних новими лінійними змінними, в результаті чого нелінійна регресія зводиться до лінійної. До нової, перетвореної регресії може бути застосований звичайний МНК.

Наприклад, у випадку поліноміальної модел з декількома пояснюючими змінними

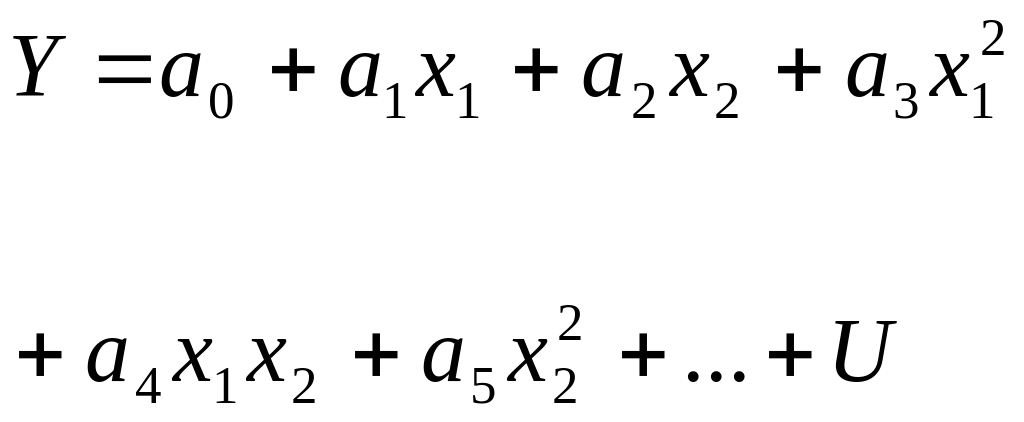
заміна , , , ... призводить до лінійної регресійної моделі.

До класу регресій, нелінійних по параметрам, що оцінюються, відносяться рівняння, в яких залежна змінна нелінійно пов’язана з параметрами. Прикладом таких регресій є функції:

-степенева: ;

-показникові: ;

-експоненціальні: .

Якщо нелінійна модель внутрішньо лінійна, то вона за допомогою відповідних перетворень може бути приведена до лінійного виду (наприклад, логарифмуванням). Якщо ж нелінійна функція внутрішньо нелінійна, то вона не може бути зведена до лінійної функції і для оцінки її параметрів використовують ітеративні процедури, успішність яких залежить від виду рівняння та особливостей ітеративного підходу, що застосовується.

31 Нелінійна регресія відносно пояснюючих змінних. Нелінійна регресія по параметрам, що оцінюються. Внутрішньо лінійна та нелінійна функції.

Розрізняють два класи нелінійних регресій:

1)нелінійні відносно пояснюючих змінних, однак лінійні по параметрам, що оцінюються;

2)нелінійні по параметрам, що оцінюються.

Клас регресій нелінійних відносно пояснюючих змінних, однак лінійних по параметрам, що оцінюються, включає рівняння, в яких залежна змінна лінійно пов’язана з параметрами. Приклад таких регресій можуть слугувати:

поліноми різних ступенів

рівностороння гіпербола

При оцінці параметрів регресії, нелінійних по пояснюючим змінним, використовується метод заміни змінних. Суть його полягає в заміні нелінійних пояснюючих змінних новими лінійними змінними, в результаті чого нелінійна регресія зводиться до лінійної. До нової, перетвореної регресії може бути застосований звичайний МНК.

Наприклад, у випадку поліноміальної моделі з декількома пояснюючими змінними

заміна , , , ... призводить до лінійної регресійної моделі.

До класу регресій, нелінійних по параметрам, що оцінюються, відносяться рівняння, в яких залежна змінна нелінійно пов’язана з параметрами. Прикладом таких регресій є функції:

степенева: ;

показникові: ;

експоненціальні: .

Якщо нелінійна модель внутрішньо лінійна, то вона за допомогою відповідних перетворень може бути приведена до лінійного виду (наприклад, логарифмуванням). Якщо ж нелінійна функція внутрішньо нелінійна, то вона не може бути зведена до лінійної функції і для оцінки її параметрів використовують ітеративні процедури, успішність яких залежить від виду рівняння та особливостей ітеративного підходу, що застосовується.

Прикладом регресії, що є внутрішньо лінійної є регресія попиту (Y) від загального доходу (z) та ціни цього товару (p):

.