21.Непрерывность сложной функции.

Непрерывность сложной функции.

X1=

X2= * {N}из к-мерного евклидова пространства

….

Xn=

Введем понятие сложной функции нескольких

переменных. Пусть функции

* заданы на множестве {N} к-мерного евклидово пространства, тогда каждой точке N с координатами N(t1, t2, …tk) поставлено в соответствие по формулам *точка М с координатами (х1, х2, …, хn) и пусть множество {M} множество таких точек. Пусть функция u=f(x1,x2,…,xn), задана на множестве {m}Еⁿ Тогда на множестве {N}}Е^k задана сложная функция u=f(x1,x2,…,Xn), где (x1, x2, …,xn) является функцией переменных (t1, t2…. Tk), определяемыми соотношениями *.

Тогда справедлива следующая теорема о непрерывности сложной функции нескольких переменных:

[T] Пусть функции * непрерывны в т. А(а1, а2, …, ак) а функция u=f(x1, x2, …xn) непрерывна в точке B(b1, b2, …bn), где bi=I(a1,a2,…ak) (I= ), тогда сложная функция u=f(1(T)….n(T) непрерывна в точке А(а1, а2, …аn)

22.Частные производные функции n переменных.

Частная производная функции нескольких переменных.

Рассмотрим функцию u=f(x1, x2,…xn), заданную на множестве {M} n- мерного евклидова пространства. И пусть точка М(x1, x2, …, xn) внутрення точка области определения множества М

Рассмотрим в данной фиксированной точке М отношения частного приращения функции 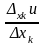(Хк0) Оно должно быть таким, чтобы вновь полученная т.М с координатами (х1, …Хк-1, Хк+Хn,Xn+1 ….Хn) принадлежала множеству М.

Существует (1)

Def Если существует предел (1) частных приращений функции функции u=f(x1, x2,…xn) в точке М с координатами (х1, х2, ….хn) по переменной Хк к соответствующему приращению Хк аргумента Хк при Хк -> 0, то этот предел называется частной производной функции в т.М по аргументу Хк и обозначается одним из следующих символов: . Частная производная представляет собой обычную производную функции. Одной переменной Хк при фиксированных значениях остальных переменных.

23.Дифференцируемость функции n переменных.

[T] Если u=f(x1,x2,x3,…,xn) дифференцируема в точке M(x1, x2,…,xn), то существуют частные производные данной функции по всем переменным, причем , где I= . Доказательство: из условий дифференцируемости функции (2) запишем: xiU=AiXi+iXi, I= . Найдем предел :

Следствия:

-условие дифференцируемости функции в точке М можно записать в виде: xkU= (5)

-если u=f(x1,x2,x3…xn) дифференцируема в точке М, то ее представление приращение в форме (2) или (3) единственно

-Если u=f(x1,x2,…xn) дифференцируема в точке М(x1, x2,…xn), то она непрерывна в каждой точке. (по 4 определению непрерывности функции

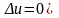
Достаточное условие дифференцируемости функции: Если функция u=f(x1, x2,…,xn) имеет частные производные по всем переменным в некоторой окрестности точки Мо( причем все частные производные непрерывны в самой точке Мо, то указанная функция дифференцируема в этой точке.

U=f(x1,x2,…xn) в точке M(x1,…,xn) записывается в виде

Функция u=f(x1,…xn) называется дифференцируемой в т М(x1, x2, …xn), если ее полное приращение представлено в виде

(2)u=A1x1+A2x2+….+AnXn +1x1+…nxn, где А1, А2, …, Аn некоторые числа, не зависящие от X1,X2….X числа, а 1, 2, …m б-м функции соответственно при х1->0, х2->0, …хm->0 Условие называется условием дифференцируемости функции в данной точке М евклидова пространства Е^m

Соотношение (2)называется условием дифференцируемости функции, причем 1=2….n=0, при Х1=Х2=Х3…Хn=0 можно записать следующим образом: u=А1 Х1+ А2 Х2)+…+ Аn Хn

Рассмотрим р=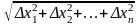 , тогда 1, х=

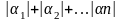| |р( р(б-м)( )(б-м)=0(р) Аналогично А1 главная часть приращения, а 0(р) б-м более высокого порядка чем р.

уравнение 2 можно записать как u=А1Х1+А2Х2+…+АnХn+0(p)

Если существует Аi0, то главной частью приращения Является А1Х1+А2Х2+…+АnХn+0(p) Она линейна относительно приращения аргумента.

Если Аi=0, I= , то главная часть также будет равна 0 и функция будет дифференцируема в данной точке по определению.