6.Теорема о представлении рациональной функции в виде суммы элементарных дробей с неопределенными коэффициентами.

Рациональная функция имеет вид , где P(x) и Q(x) многочлены, причем P(x) многочлен степени n, q(x) многочлен степени m.

1.nm, то делением многочлена на многочлен мы выделяем целую часть и дробную часть =W(x)+ 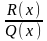, где W(x)- некоторый многочлен, а R(x) многочлен степени ниже чем Q(x)

2.n<m то применяют метод неопределенных коэффициентов

Q(x)=A(x-a₁)^₁ (x-a₂)^_2….. (x-a_k)^_k (если D>=0, т.е. можно разложить)

Или

Q(x)=(x²+p₁x+q₁)^1 (x²+p₂x+q₂)^2……… (x²+p_lx+q_l)^{l (3)}

[Т] Каждый многочлен может быть представлен в виде Q(x)=A(x-a₁)^₁ (x-a₂)^_2….. (x-a_k)^_k Или Q(x)=(x²+p₁x+q₁)^1 (x²+p₂x+q₂)^2……… (x²+p_lx+q_l)^l

[Т] Если рациональная функция имеет степень многочлена числителя n меньше, чем степень многочлена знаменателя m и многочлен Q(x) имеет вид (3), то эту функцию можно единственным образом представить в виде:

= … … … …+ …

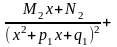7.Метод неопределенных коэффициентов.

Метод неопределенных коэффициентов

Он заключается в том, чтобы следовать алгоритму: Записать представление 1, привести правую часть к общему знаменателю и группировать при степенях Х, получим дроби с равными знаменателями, присваиваем числители. Получим 2 многочлена, они равны если равны коэффициенты при соответствующих степенях Я, следовательно составляем систему уравнений, приравнивая коэффициенты при соответствующих степенях Х.

8.Основные типы интегралов от рациональных функций.

Основные типы интегралов, берущихся по частям.

1.А/х-а dx= Ad(x-a)/x-a=Aln|x-a|+C

2.Аdx/(х-а)^k=A (х-а)^-kd(x-a)=A(x-a)^1-k/1-k+C (k1)

3. dx=M/2 +N =M/22x+p/x²+px+q dx +(N-MP/2)dx/ x²+px+q=M/2ln| x²+px+q|+(N-MP/2)dt/t²+a²

x²+px+q=( x²+2p/2x+p²/4)+q-p²/4=(x+p/2)²+(q-p/4)=т.е.  dx=M/2(x²+px+q)^-kd(x²+px+q)+(N-Mp/2)

dt/(t²a²)^k=M/2(x²+px+q)^1-k/1-k +(N-MP/2)Ik

Рекуррентная формула

Ik=…….Ik-1

Рекуррентная формула доказывается с помощью интегрирования по частям

Ik=1/2a²(k-1) (t/(t²a²)^k+(2k-3) dt/(t²a²)^k-1 ) (K>2)

9.Понятие интегральной суммы. Геометрический смысл.

Рассмотрим функцию f(x) определенную в каждой точке сегмента [a,b], a<b

Def Будем говорить, что задано разбиение сегмента [a,b] если заданы точки х_0, х_{1, ….,} х _{n, .}

Такие что а= х_0< х_1< х _2<….< х _n=b. { х _n }- разбиение х _n . Рассмотрим на сегменте [a,b] функцию f(x) принимающую в каждой точке сегмента конечные значения. По данному разбиению {x_k} построим ( х _к; _к)= (1)

 _к[x_k-1;x_k] , полученное число называют интегральной суммой. Она зависит от способа разбиения Xk и от выбора точек  _к Отрезки получающиеся в результате разбиения [x_k-1;x_k] называются частичными отрезками.  х_к =х_к-х_к-1 – длина частичного отрезка

И тогда интегральную сумму (1) можно записать в виде (х_к;_к)= (2)

Диаметр разбиения: максимальная длина частичного отрезка называется диаметром разбиения и обозначается числом d. d=max х_к

Геометрический смысл интегральных сумм:

F(₁)*x₁=S прямоугольника 1

F(₂)*x₂=S прямоугольника 2

f(₁)*x₁+f(₂)*x₂+…. f(n)*x_n=( х_к;_к)=S*

где S* площадь ступенчатой фигуры, т.е. интегральная сумма (2) равна S* Если мы устремим диаметр d к 0, S* будет стремится к площади криволинейной трапеции, т.е. фигурой ограниченной снизу сегментом [a,b], сверху неотрицательной функцией f(x), с боков прямыми x=a, x=b.

x

Xo=a (1) (X1) (2) (X2) (x _{k-1 )} (k) x_k (x_n-1) n ( b=x_n)

Геом.смысл:  - сумма площадей прямоугольников с основаниями Х1, Х2,…  Хn и высотами f (₁), f(₂)…f(_n).

S*= f(_k)*  Хk. Т.о. интегральная сумма представляет собой

площадь ступенчатой фигуры. Но если d0 (n ), то

S* = f((_k ; Xk) = f(x)dx = S криволин. трапеции