30.Локальный экстремум функции n переменных. Необходимое условие локального экстремума.

DEF будем говорить, что функция u=f(M) Df=f{M}сЕ ⁿ имеет в точке Мо локальный максимум (минимум) если существует такая - окрестность этой точки в пределах которой значение функции f(Mo) является наибольшим (наименьшим) по сравнению со значениями функции в любой другой точке этой окрестности.

Необходимое условие локального экстремума

Если функция u=f(x1,x2…xn) имеет в точке Mo( частные производные первого порядка по всем переменным Х1,Х2,Х3…Хn и имеет в т Мо локальный экстремум, то все частные проиводные первого порядка в точке Мо обращаются в 0.

Все точки в который частные производные обращаются в 0, в которых все необъодимые условия экстремума выполнены, называются стационарными точками.

Замечание: необходимое условие экстремума может быть записано так: Если функция u=f(m) дифференцируема в точке Мо и имеет в этой точке локальный экстремум, то дифференциал функции du(Mo)=0(тождественное равенство), т.е.

31.Достаточные условия локального экстремума функции n переменных.

Пусть функция u=f(M) один раз дифференцируема в некоторой окрестности точки Мо и два раза дифференцируема в самой точке Мо, пусть кроме того Мо – стационарная точка. Тогда:

1.Если d²u в точке Мо положительно определенная квадратичная форма относительно переменных dx1,dx2,…,dxn, то Мо – точка локального минимума

2.Если d²u в точке Мо отрицательно определенная квадратичная форма, то Мо – точка локального Максимума.

3.Если d²u в точке Мо знакопеременная квадратичная форма, то экстремум в точке Мо не существует.

Частный случай:

[Т] пусть функция u=f(x,y) один раз дифференцируема в окрестности точки Мо с координатами (хо,уо) и два раза дифференцируема в самой точке Мо и пусть Мо – стационарная точка, тогда если в точке Мо выполнено условие:

, то функция имеет в точке Мо локальный экстремум, причем если в точке Мо>0 , то Мо точка локального минимума.

Если (Мо)<0 то Мо точка локального Max

Если же то экстремум в точке Мо не существует.

32.Неявные функции.

Def Если переменная u, являющаяся по смыслу функцией переменных х1,х2,…,хn задается посредством функций уравнений F(U,X1,x2,…,xn)=0, то говорят, что функция задана неявно.

Частные производные неявно заданной функции вычисляются по формулам:

Рассмотрим совокупность М неявных функций, которые задаются посредством системы М функциональных уравнений:

(1)

Пусть функции определены, как решение М функциональных уравнений (2)

(2)

Решением системы (2) будет называться совокупность функций, таких что при их подстановки в систему все уравнения этой системы образуются в тождества.

Def Это решение будем называть непрерывным и дифференцируемом в некоторой области D изменения переменных Х1,Х2,…Хn Если каждая из функций U1,U2,…Um непрерывна и дифференцируема в этой области.

=

Такой определитель называют определителем Якоби или Якобианом.

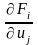[T] Система (2) будет разрешима, а решение непрерывно и дифференцируемо, если функция f1,f2,…,fn дифференцируема в окрестности точки Мо, непрерывна в точке Мо, Якобиан отличен от 0 и F1=F2=…=Fn в точке Мо