1. Понятие первообразной. Основные свойства (лемма, теорема)

Def Функция F(x) называется первообразной для функции f(x)на некотором промежутке Х, если для любого х Х выполняется условие F’(x)=f(x). Например, функция F(x)=sinx является первообразной для функции f(x)=cosx на всей прямой, т.к. при любом значении x(sinx)’=cosx

Лемма: Функция, производная которой на некотором промежутке Х равна 0 постоянна на этом промежутке. f’(x)=0(xX), то f(x)=c

Док-во: пусть во всех т. промежутка Х f’(x)=0, тогда для любых 2-х точек 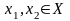функция f(x) определена и непрерывна на [x1,x2] и дифференцируема на (x1,x2) и существует точка (x1,x2) такая, что выполняется Т. Лагранжа, т.е. f(x2)-f(x1)=f’()(x2-x1), где x1<<x2. Т.к. f’()=0, то f(x2)=f(x1)=0, т.е. значения функции во всех точках промежутка одинаковы, т.е. f(x)=С, где С- некоторое число.

[Т] Если F(x)- первообразная для функции f(x) на некотором промежутке Х, то любая другая первообразная для f(x) на том же промежутке может быть представлена в виде F(x)+C, где С- произвольная постоянная.

Док-во: Пусть F(x)- первообразная для функции f(x) на некотором промежутке Х, т.е. F’(x)=f(x). Пусть Ф(х) некоторая другая первообразная для функции f(x) на промежутке Х, т.е. Ф’(x)=f(x). Тогда для любого хХ (Ф(x)-F(x))’=Ф’(x)-F’(x)=f(x)-f(x)=0 Т.о. мы получили, что производная функции равна 0, а это означает по лемме, что функция Ф(х)-F(x) постоянна, т.е. Ф(х)-F(x)=С, на промежутке Х, где С- некоторое число. Следовательно, Ф(х)=F(x)+C.

Следствие 1: множество функций F(x)+C, где F(x) одна из первообразных для функции f(x),а С- произвольная постоянная исчерпывает все множество первообразных функций для f(x)

2. Понятие неопределенного интеграла.

Def Если функция F(x) является первообразной для функции f(x) на промежутке Х, то множество функций {F(x)+C}, где С- произвольная постоянная называется неопределенным интегралом от функции f(x) на этом промежутке и обозначается символом f(x)dx=F(x)+C. При этом f(x) называется подынтегральной функцией, f(x)dx- подынтегральным выражением, а переменная х- переменная интегрирования. f(x)dx- выражает множество всех первообразных для функции f(x) на промежутке Х.

Def Восстановление функции по ее производной или что тоже самое: отыскание неопределенного интеграла называется интегрированием этой функции, т.к. F’(x)=f(x) F’(x)dx=F(x)+C

Интегрирование- операция обратная дифференцированию и правильность интегрирования определяется следующим образом: мы должны продифференцировать результат и если получили подынтегральную функцию, то операция выполнена верно.

Основные свойства неопределенного интеграла:

1.Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е. (f(x)dx)’=f(x) и d( f(x)dx)=f(x)dx Доказательство: (f(x)dx)’=(F(x)+C)’=F’(x)=f(x) и df(x)dx=(f(x)dx)’dx=f(x)dx

2.d(f(x)dx)=f(x)dx

Док-во: d(f(x)dx)=d(F(x)+C)=(F(x)+C)’dx=F’(x)dx=f(x)dx

3.Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е. dF(x)=F(x)+C. Доказательство: т.к. dF(x)=F’(x)dx, то по определению F'(x)dx=F(x)+C

4.Постоянный множитель можно вынести из-под знака интеграла, т.е. если k=const0, то kf(x)dx=kf(x)dx. Доказательство: пусть F(x) первообразная для f(x) на промежутке Х, т.е. xX F’(x)=f(x)kF(x) первообразная для kf(x), т.е. (kF(x))’=kF’(x)=kf(x). Из определения следует, что kf(x)dx=k[F(x)+C]=kF(x)+C1=kf(x)dx, где С1=кС, ч.т.д.

5.Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций отдельно, т.е. (f(x)g(x))dx=f(x)dxg(x)dx. Доказательство: пусть F(x) и G(x) являются первообразными для функций f(x) и g(x) на промежутке Х, т.е. хХ F’(x)=f(x), G'(x)=g(x). Тогда функции F(x)G(x) являются первообразными для функция f(x)g(x). Следовательно, f(x)dxg(x)dx=(F(x)+C1)(G(x)+C2)=(F(x)G(x))+(C1C2)=[F(x)G(x)]+C=(f(x)g(x))dx

Это свойство справедливо для любого конечного числа слагаемых.