12.Интеграл с переменным верхним пределом.

Интеграл с переменным верхним пределом.

x  [a,b]

Это интеграл у которого нижний предел а=const а верхний предел х переменный. Величина этого интеграла представляет собой функцию верхнего предела х

(х)= , где х принадлежит сегменту [a,b] и ф(х)= интеграл с переменным верхним пределом. Геометрически интеграл с переменным верхним пределом представляет собой S криволинейной трапеции.

[Т] Производная интеграла от непрерывной функции по переменному верхнему пределу существует и равна значению подынтегральной функции в точке, равной верхнему пределу, т.е. Ф’(x)=( )’_x=f(x)

Ф’(x)=( )’=f(x)

Ф’(x)=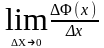

Доказательство:

1 вариант (учебники): возьмем любое значение x[a,b] и придадим ему приращение 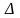х0 такое, чтобы х+ х[a,b], т.е. ax+ хb. Тогда функция Ф(х) по определению получит новое значение: Ф(х+ х)=

Согласно второму свойству определенного интеграла, имеем: Ф(х+ х)= + =Ф(х)+ Ф=Ф(х+Х)-Ф(х), т.к. f(x) непрерывна на [a,b] то существует число c[x, x+x]:[ =f(c)x]. Если устремить приращение аргумента к нулю, получим : =f(x) или Ф’(х)=f(x), ч т.д. Можно записать, что f(x)dx=Ф(x)+C= +C

2 вариант (Деревенских) Ф’(х)= Ф(х)= - = + - = =f(c)* x. По теореме о среднем существует c[x, x+x]

Ф’(x)= Отсюда следует, что Ф’(x)=f(x)

13.Формула Ньютона-Лейбница.

Формула Ньютона- Лейбница

Пусть функция f(x) непрерывна на отрезке [a,b] и имеет на этом отрезке семейство первообразных, одной из которых является Ф(х)= .

[Т] Если функция f(x) непрерывна на [a,b], то верно следующее равенство . Т.е. определенный интеграл от непрерывной функции равн разности значений любой ее первообразной на верхнем и нижнем пределах интегрирования соответственно. Она называется формулой Ньютона-Лейбница.

Доказательство: Пусть F(x) другая первообразная для функции f(x) на том же отрезке, которая отличается от Ф(х) не более чем на константу, т.е. Ф(х)=F(x)+C, =F(x)+C, где С- некоторое число, axb. Подставляя в это равенство значение х=а и используя свойство 1, имеем: =0, получим: 0= , F(a)+C, C=-F(a)

Т.е. для любого х[a,b] Полагая здесь х=b получим искомую формулу.

14. Замена переменных в определенном интеграле.

Замена переменных в определенном интеграле

[T] пусть функция f(x) непрерывна на сегменте [a,b] и пусть выполнены следующие условия:

1.функцию х=(t) дифференцируема на [,] и ’(t) непрерывна на [,]

2.Множеством значений функции х=(t) является отрезок [a,b]

3.()=a и ()=b, то справедлива формула

Доказательство: По формуле Ньютона- Лейбница: , где F(x)-какая-нибудь первообразная для функции f(x) на [a,b]. С другой стороны, рассмотрим сложную функцию Ф(t)=F((t)) Согласно правилу дифференцирования сложной функции находим: Ф’(t)=F’((t))*’(t)=f((t))’(t). Отсюда следует, что функция Ф(t) является первообразной для функции f((t))’(t), непрерывной на [,] и поэтому согласно формуле Ньютона-Лейбница получаем, = Ф()-Ф()=F(())-F(())=F(b)-F(a)=

Это формулы замены переменной или подстановки в определенном интеграле.

Замечание1. Если при вычислении неопределенного интеграла с помощью замены переменной мы должны были от новой переменной t возвращаться к старой переменной х, то при вычислении определенного интеграла этого можно не делать, т.к. цель- найти число, которое в силу доказанной формыл равно значению каждого из рассматриваемых интегралов.