
- •Приближенные числа
- •Правила вычислений с приближенными числами.
- •Приближенное решение алгебраических и трансцендентных уравнений. Отделение корней и уточнение приближенных корней. Графическое решение уравнений.
- •Метод половинного деления (метод «вилки»).
- •Метод хорд.
- •Метод Ньютона (метод касательных).
- •Метод итерации. Приведение уравнений к виду, удобному для итерации.
- •Приближенное решение систем линейных уравнений. Метод итераций.
- •Приближенное решение систем нелинейных уравнений. Метод итерации.
- •Постановка задачи интерполирования функций. Общее решение задачи интерполирования функции полиномом.
- •Интерполяционная формула Лагранжа
- •Интерполирование сплайнами
- •14 Аппроксимирование функций (15 не нашли)
- •Аппроксимирование функций. Метод ортогональных функций.
- •Квадратурная формула Ньютона-Котеса
- •Квадратурная формула Гаусса
- •Численные метода решения задачи Коши для обыкновенных дифференциальных уравнений. Метод Эйлера. Метод Эйлера-Коши
- •Метод Рунге-Кутта
- •Редукция к задаче Коши двухточечной краевой задачи для линейного уравнения второго порядка.
- •Метод коллокации.
- •23.Аппроксимация производных конечно-разностными соотношениями.
- •Метод конечных разностей численного решения обыкновенных дифференциальных уравнений.
- •Принципы построения сеток на плоскости и в пространстве.
- •26. Построение разностных схем для уравнений параболического типа.
- •27. Экстремумы функций. Классификация методов безусловной оптимизации.
- •28. Общая характеристика методов оптимизации нулевого порядка.
- •Метод прямого поиска (метод Хука-Дживса).
- •Метод деформируемого многогранника (метод Нелдера-Мида).
- •Метод вращающихся координат (метод Розенброка).
- •Метод параллельных касательных (метод Пауэлла).
- •Общая характеристика методов оптимизации первого порядка.
- •34.Метод наискорейшего спуска
- •35. Общая характеристика методов оптимизации второго порядка. Метод Ньютона.
- •36. Метод Ньютона с регулировкой шага (метод с переменной метрикой)
- •37. Метод статистических испытаний (метод Монте-Карло)
- •38. Вычисление кратных интегралов методом Монте-Карло
- •39. Структура искусственной нейронной сети (инс)
- •40. Компьютерная модель нейрона (нейроэлемента, нэ)
- •41. Функции активации нейроэлементов
- •45.Методы обучения элементарного перцептрона.
- •46.Многослойный перцептрон.
- •47. Понятие обучающей выборки.
Метод итерации. Приведение уравнений к виду, удобному для итерации.
Метод итерации является универсальным: его можно применять для решения обширного класса как линейных, так и нелинейных уравнений. Сущность этого метода заключается в следующем. Пусть дано уравнение , (5)
где
-
непрерывная функция, и требуется найти
его вещественные корни. Преобразуем
уравнение (5) в эквивалентное уравнение
вида
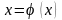 . (6)
. (6)
Выберем начальное приближение
x0
и, подставив его в правую часть уравнения
(6), получим число
 .
Затем вычислим
.
Затем вычислим
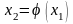 и т. д. Получим последовательность чисел
и т. д. Получим последовательность чисел
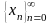 ,
определяемую равенством
,
определяемую равенством
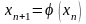 ,
n = 0, 1,
2,... (7)
,
n = 0, 1,
2,... (7)
Для того, чтобы последовательность
сходилась к корню с
уравнения (5), необходимо выполнение
условия сходимости: если
функция
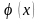 определена и дифференцируема на отрезке
[a,
b] и
определена и дифференцируема на отрезке
[a,
b] и
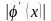
q<1 при
всех a
x
b, то
процесс итерации
,
n = 0, 1, 2,...
сходится к корню с уравнения
независимо от начального значения.
q<1 при
всех a
x
b, то
процесс итерации
,
n = 0, 1, 2,...
сходится к корню с уравнения
независимо от начального значения.
Условие сходимости метода итерации q<1, (8)
где q – максимальное значение производной на интервале, в котором находится корень уравнения (если корней несколько, то условие сходимости должно выполняться для каждого интервала).
Чем ближе к нулю максимальное значение производной q, тем выше скорость сходимости метода.
Замечание.
Пусть в некоторой окрестности [a,
b] корня с
уравнения
производная
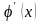 сохраняет постоянный знак и выполнено
неравенство
q<1.
Тогда, если производная
положительна, т. е. 0
q<1,
то последовательные приближения
,
n = 0, 1,
2,...,
сохраняет постоянный знак и выполнено
неравенство
q<1.
Тогда, если производная
положительна, т. е. 0
q<1,
то последовательные приближения
,
n = 0, 1,
2,...,
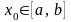 сходятся к корню монотонно. Если же
производная
отрицательна, т.е. 1<q
0
то последовательные приближения
колеблются около корня с.
сходятся к корню монотонно. Если же
производная
отрицательна, т.е. 1<q
0
то последовательные приближения
колеблются около корня с.
Для метода итерации большое
значение имеет способ преобразования
уравнения (5) к виду (6), т. е. выбор функции
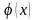 ,
которая должна подчиняться условию
сходимости
q<1.
,
которая должна подчиняться условию
сходимости
q<1.
Рассмотрим один достаточно общий прием приведения уравнения (5) к виду (6), для которого обеспечено выполнение неравенства (8).
Пусть искомый корень лежит
в интервале [a, b],
причем 0 <m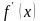 M, (9)
M, (9)
для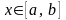 ,
где m –
наименьшее значение производной
на [a, b],
а M –
наибольшее значение производной
на [a, b].
,
где m –
наименьшее значение производной
на [a, b],
а M –
наибольшее значение производной
на [a, b].
Если производная
отрицательна, то вместо уравнения
рассматриваем уравнение
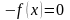 .
.
Заменим уравнение (5) эквивалентным уравнением вида
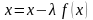 ,
>0. (10)
,
>0. (10)
Сравнивая (10) и (6), видим, что
 .
.
Так как метод итерации должен быть сходящимся и для функции должно выполняться условие (8), то будем иметь
0
=
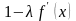 q<
1. (11)
q<
1. (11)
Учитывая выражение (9), получим следующую оценку:
0 
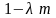 q. (12)
q. (12)
Можно положить:
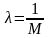 (13)
(13)
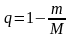 <
1. (14)
<
1. (14)
В методе итерации в качестве начального приближения чаще всего принимается один из концов интервала [a, b].
Оценка погрешности n-го
приближения
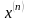 к корню с
уравнения такова:
к корню с
уравнения такова:
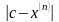
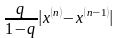 , (15)
, (15)
где
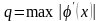 на [a, b].
на [a, b].
Замечание1.
При нахождении корня уравнения
с заданной точностью
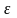 >0
или при оценке погрешности n-го
приближения
можно, не вычисляя точного значения
числа
на [a, b],
ограничиться следующей практической
рекомендацией:
>0
или при оценке погрешности n-го
приближения
можно, не вычисляя точного значения
числа
на [a, b],
ограничиться следующей практической
рекомендацией:
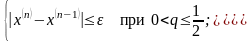 (16)
(16)
Замечание2. Преимущество метода итерации заключается в том, что сходимость процесса не зависит от выбора начального приближения . Отдельная ошибка, допущенная при вычислениях, не выводящая за пределы отрезка [a, b], не повлияет на конечный результат. Здесь мы встречаемся со свойством самоисправляемости сходящегося итерационного процесса.
Пример 1.
Методом итерации решить
уравнение
 .
.
Графически отделяя корни данного уравнения, заключаем, что уравнение имеет единственный действительный корень, принадлежащий отрезку 1,1; 1,2.
Преобразуем данное уравнение
к виду (6) следующим образом:
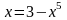 .
При таком преобразовании функция
.
При таком преобразовании функция
 .
Проверим выполнение условия сходимости
(8).
.
Проверим выполнение условия сходимости
(8).
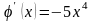 .
.
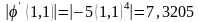 1
1
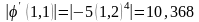 1.
1.
Видно, что условие сходимости (8) не выполняется и такое преобразование не подходит, т. к. метод будет расходиться.
Пример 2.
Методом итерации найти решение
уравнения
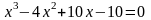 .
(17)
.
(17)
При помощи графического метода отделим корни уравнения, т. е. найдем интервалы, в каждом из которых содержится единственный корень уравнения. Данное уравнение имеет один действительный корень, который содержится в интервале 1,6; 1,7.
Проверим условие нахождения
корня в интервале
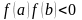 :
:
f(1,6) = - 0,144 0,
f(1,7) = 0,353 0.
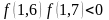 ,
следовательно, корень данного уравнения
действительно содержится в интервале
1,6;
1,7.
,
следовательно, корень данного уравнения
действительно содержится в интервале
1,6;
1,7.
Преобразуем уравнение к виду : (18)
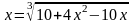 . (19)
. (19)
Сравнивая (18) и (19), видим, что
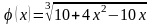 .
.
Проверим выполнение условия сходимости q<1,
где q – максимальное значение производной на интервале 1,6; 1,7.
 ≈
0,356 <1,
≈
0,356 <1,
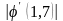 ≈
0,436 <1.
≈
0,436 <1.
Условие сходимости выполняется
и корень уравнения можно уточнять,
используя итерационную формулу
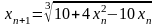 .
.
= 1,6.
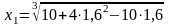 = 1,61853,
= 1,61853,
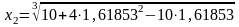 = 1,62528,
= 1,62528,
x3 = 1,62781, x4 = 1,62877, x5 = 1,62913, x6 = 1,62927, x7 = 1,62932, x8 = 1,62934, x9 = 1,62935,
x10 = 1,62935, x11 = 1,62936, x12 = 1,62936.
Корень уравнения x = 1,62936.
Можно предложить еще такой
способ: представим исходное уравнение
в виде
 .
.
Отсюда
 .
.
Сравнивая полученное выражение
и (6), видим, что
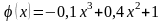 .
.
Проверим условие сходимости
(8):
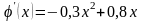 .
.
= 0,512 <1,
= 0,493 <1.
Условие сходимости выполняется
и корень уравнения можно уточнять,
используя формулу
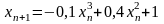 .
= 1,6.
.
= 1,6.
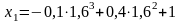 = 1,6144,
= 1,6144,
 = 1,62175,
= 1,62175,
x3 = 1,62550, x4 = 1,62740, x5 = 1,62836, x6 = 1,62885, x7 = 1,62910, x8 = 1,62923, x9 = 1,62929,
x10 = 1,62932, x11 = 1,62934, x12 = 1,62935, x13 = 1,62936, x13 = 1,62936. Корень уравнения x = 1,62936.
