1. Приближенные числа

Классификацияпогрешностей:

1. Данные, значение которых в принципе может быть представлено целым числом, но точное его определение затруднительно.

2. Экспериментальные данные, значение которых мы не можем измерить с абсолютной точностью.

3. Величины (напримерe, π), которые не имеют абсолютно точных значений.

Источники погрешности решения задачи:

1. Математическое описание задачи является неточным, в частности, неточно заданы исходные данные описания. Это неустранимая погрешность.

2. Применяемый для решения метод часто не является точным: получение точного решения задачи требует неограниченного или неприемлемо большого числа арифметических операций, и поэтому вместо получения точного решения приходится прибегать к приближенному. Это погрешность метода.

3. При выполнении арифметических операций на компьютере или любым другим образом, как правило, производятся округления. (Это же относится к вводу чисел в память компьютера и выводу полученных результатов.) Это вычислительная погрешность.

Если a – точное значение некоторой величины, а a* – известное приближение к нему, то абсолютной погрешностью приближения a* называют величину Δ(a*), удовлетворяющую неравенству: |а*-а|≤∆(а*).

Относительной погрешностью называют величину δ(a*), удовлетворяющую неравенству:|(а*-а)/а*| ≤ δ(а*). Относительнуюпогрешностьчастовыражают в процентах.

2. Правила вычислений с приближенными числами.

Погрешность суммы

Пусть задана функция у = f(х₁,х₂) = х₁ + х₂

Для абсолютной погрешности получаем ∆(у*) = ∆(х₁*) + ∆(х₂*)

Относительная погрешность δ(у*) = (∆(х₁*) + ∆(х₂*))/(х₁* + х₂*) = (δ(х₁*)·х₁* + δ(х₂*)·х₂*)/( х₁* + х₂*).

Погрешность разности

Пусть задана функция у = f(х₁,х₂) = х₁ - х₂

Для абсолютной погрешности получаем ∆(у*) = ∆(х₁*) + ∆(х₂*)

Относительная погрешность δ(у*) = (∆(х₁*) + ∆(х₂*))/(х₁* - х₂*).

Если х₁* и х₂* близки, относительная погрешность δ(у*) может оказаться много больше δ(х₁*) и δ(х₂*).

Погрешность произведения

Пусть задана функция у = f(х₁,х₂) = х₁ · х₂

Для абсолютной погрешности получаем ∆(у*) = |х₂*|·∆(х₁*) + |х₁*|·∆(х₂*)

Относительная погрешность δ(у*) = ∆(у*)/(| х₁*· х₂*|) = ∆(х₁*)/|х₁*| + ∆(х₂*)/|х₂*| = δ(х₁*) + δ(х₂*).

Погрешность частного

Пусть задана функция у = f(х₁,х₂) = х₁/х₂

Для абсолютной погрешности получаем ∆(у*) = (1/|х₂*|)·∆(х₁*) + (|х₁*|/|х₂*|²)·∆(х₂*)

Относительная погрешность δ(у*) = ∆(х₁*)/|х₁*| + ∆(х₂*)/|х₂*| = δ(х₁*) + δ(х₂*).

Рассмотренные только что оценки относились к «Прямой задаче погрешностей» -- нахождение погрешности функции по погрешностям аргументов.

Обратная задача теории погрешностей -- нахождение допустимой погрешности аргументов, при которой погрешность значений функции будет не более заданной величины ε.

В общем случае Обратная задача математически некорректна. Возможно, однако, рассмотрение некоторых частных случаев.

Используем неравенство

Должно быть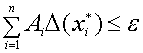

При n = 1 ∆(х₁*) ≤ ε/А₁

При n> 1

a) еслипогрешности одинаковы, D(x₁) = … = D(x_i) = D, то ∆≤ ε/∑А_i

b) есливклады в погрешность результата одинаковы А₁·∆(х₁*) = … = A_n·∆(х_n*) = ε/n, тогда ∆(х_i*) = ε/(A_i·n).