Подрезание эвольвентных зубьев в станочном зацеплении

В процессе формирования эвольвентного зуба по способу огибания, в зависимости от взаимного расположения инструмента и заготовки возможно срезание эвольвентной части профиля зуба той частью профиля инструмента, которая формирует переходную кривую. Условие, при котором это возможно определяется из схемы станочного зацепления. Участок линии зацепления, соответствующий эвольвентному зацеплению определяется отрезком . где точка определяется пересечением линии станочного зацепления и прямой граничных точек инструмента. Если точка располагается ниже точки , то возникает подрезание зуба. Условие, при котором нет подрезания, можно записать так:

.

Запишем это соотношение исходя из размеров зубчатого колеса.

Из : .

Из :

Тогда

Если нарезаемое колесо – нулевое, без смещения т.е. ,то . Таким образом - минимальное число зубьев нулевого колеса, которое может быть нарезано без подреза стандартным реечным инструментом.

Избежать подрезания колеса можно, если увеличить смещение инструмента так, чтобы точка оказалась бы выше точки или совпала с ней. Тогда смещение инструмента, при котором не будет подрезания можно определить из полученного ранее выражения для числа зубьев:

, так как , то окончательно получим:

В предельном случае, когда точка совпадает с точкой : .

Для стандартного реечного инструмента: ,

где - минимальное смещение инструмента, при котором нет подрезания.

Таким образом, условие отсутствия подреза можно записать в виде .

Из анализа полученных выражений следует, что

• Если нарезаемое колесо с числом зубьев меньше 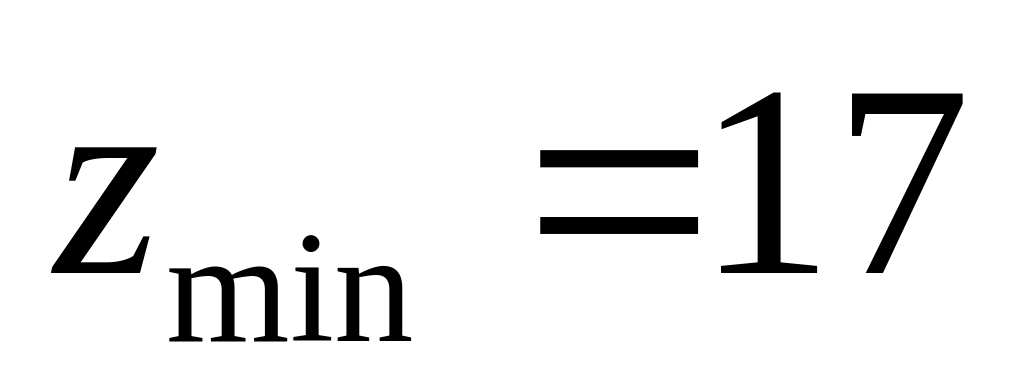, то такое колесо может быть только положительным ;

• Если нарезаемое колесо с числом зубьев , то такое колесо может быть положительным и нулевым ;

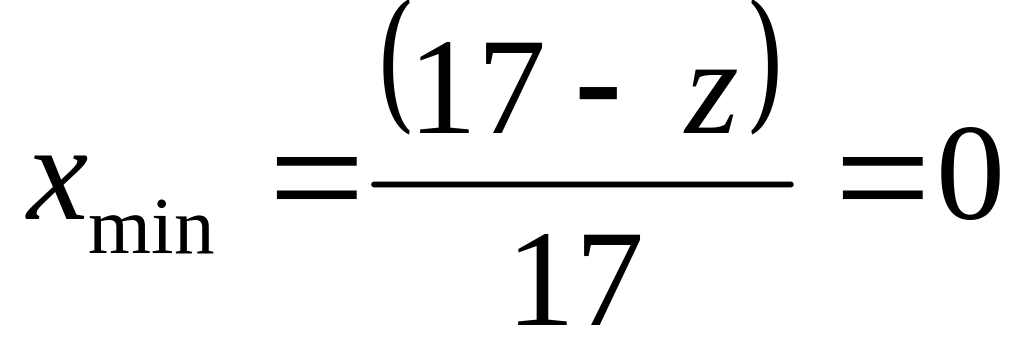• Если нарезаемое колесо с числом зубьев больше , то такое колесо может быть положительным, отрицательным и нулевым ;

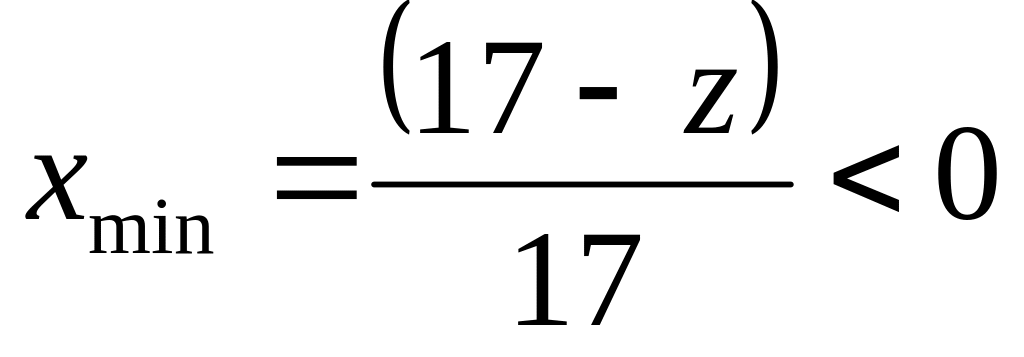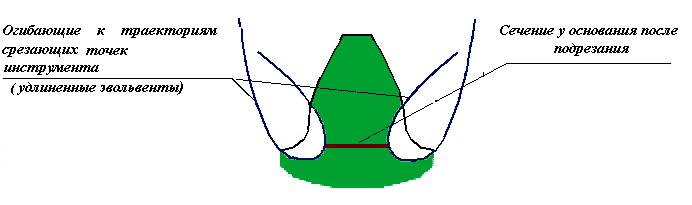
Понятие о области существования зубчатого колеса.

Параметры в зубчатых передачах удобно разделять на параметры зубчатого колеса и параметры зубчатой передачи. Параметры зубчатого колеса характеризуют данное зубчатое колесо и, как составная часть, входят в параметры зубчатой передачи, образованной этим колесом с другим парным ему колесом. К параметрам зубчатого колеса относятся: число зубьев, модуль, параметры исходного контура инструмента, которым оно обрабатывалось и коэффициент смещения. Как отмечено выше, на выбор этих параметров накладываются ограничения по заострению и подрезанию зуба. Поэтому можно ввести понятие области существования зубчатого колеса - диапазона коэффициентов смещения, при которых не будет подрезания и заострения. Т.е расчетный коэффициент смещения должен удовлетворять следующему неравенству:

При - зона подреза зубьев колеса, при - зона заострения.

На рис. показан пример такой области существования.

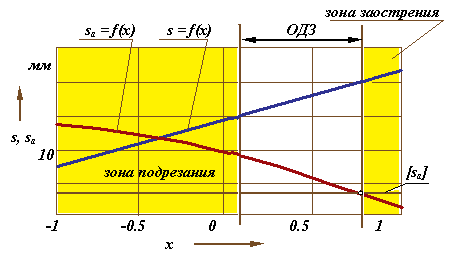
Если , то зона подреза перекрывается с зоной заострения то рабочее зубчатое колесо с числом зубьев реечным инструментом с такими параметрами получено быть не может. В любом случае колесо получится бракованным.

Эвольвентная зубчатая передача

Цилиндрическая эвольвентная зубчатая передача.

Два зубчатых колеса с одинаковым модулем и с числами зубьев соответствующими заданному передаточному отношению образуют зубчатую передачу или простейший зубчатый механизм. В этом трехзвенном механизме зубчатые колеса образуют между собой высшую пару, а со стойкой низшие пары. Зубчатая передача, кроме параметров образующих ее колес, имеет и собственные параметры: угол зацепления , межосевое расстояние , воспринимаемое смещение и уравнительное смещение . Элементы эвольвентного зубчатого зацепления

1. Полюс зацепления – мгновенный центр вращения в относительном движении соприкасающихся профилей.

2. Линия зацепления (теоретическая часть) – отрезок , определяющий предельную длину образующей прямой, проходящей через полюс зацепления (общая касательная, проведенная к основным окружностям зубчатых колес, находящихся в зацеплении через полюс зацепления).

3. Практическая линия зацепления (активная часть) – отрезок , определяющий начало и конец зацепления. Точки - вход – выход из зацепления – точки пересечения линии зацепления с окружностями вершин.

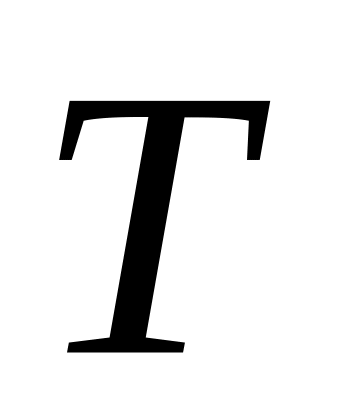4. Дуга зацепления - расстояние, проходимое точкой боковой поверхности зуба от момента входа в зацепление до момента выхода, может быть измерено по дуге любой окружности.

5. Угол зацепления - угол между линией зацепления и перпендикуляром к линии центров, восстановленным в полюсе зацепления, численно равен углу давления.

6. Межосевое расстояние .

7. Стандартный радиальный зазор - расстояние между окружностями вершин одного колеса и окружностями впадин второго, измеренное по линии центров. Величина постоянная для данного зацепления.

8. Воспринимаемое смещение - Расстояние между делительными окружностями колес, входящих в зацепление, измеренное по линии центров.

9. Уравнительное смещение - условная расчетная величина, введенная в расчет геометрии зацепления с целью обеспечения стандартного радиального зазора в зацеплении (величина, выражающая в долях модуля уменьшение радиуса окружностей вершин колес, необходимое для обеспечения стандартной величины радиального зазора). Это расстояние от граничной прямой рейки до окружности вершин колеса.

10. Рабочий профиль – боковая сторона зуба, которая при заданном направлении вращения передает и воспринимает усилие. Активная часть рабочего профиля – часть боковой поверхности зуба, участвующая в зацеплении (на чертеже обозначается штриховкой).

Передаточное отношение механизма , числа зубьев колес и , начальные окружности , (или центроиды) и межосевое расстояние связаны между собой следующими соотношениями (см. основную теорему зацепления и раздел по кинематике зубчатой передачи):