Эвольвентное зацепление и его свойства.

В зубчатой передаче контактирующие элементы двух профилей выполняются по эвольвентам окружности и образуют, так называемое эвольвентное зацепление.

Параметры эвольвентного зацепления

Рассмотрим для начала параметры эвольвентного зацепления (при этом все параметры, возникающие в процессе зацепления, имеют индекс ).

1. Линия зацепления.

прямой , которая носит название теоретической линии зацепления. Т.е. эвольвенты касательны друг к другу только внутри теоретической части линии зацепления, вне этого отрезка эвольвенты пересекаются, происходит так называемое наложение эвольвент. При качении одной эвольвенты другой все рано от к или наоборот точка контакта движется по линии зацепления.

2. Начальные окружности

, - окружности проходящие через полюс зацепления , катятся без проскальзывания во время контакта эвольвент. Из основной теоремы зацепления Виллиса очевидно, что

3. Угол зацепления

- угол между линией зацепления и нормалью восстановленной в полюсе зацепления к эвольвентным профилям численно равен углу давления. - передаточное отношение

4. Межосевое расстояние

В связи со всем вышесказанным эвольвентное зацепление обладает рядом полезных свойств, которые и определяют широкое распространение эвольвентных зубчатых передач в современном машиностроении. Рассмотрим эти свойства.

С войства эвольвентного зацепления

Свойство 1. Передаточное отношение эвольвентного зацепления определяется только отношением радиусов основных окружностей и является величиной постоянной.

Свойство 2. При изменении межосевого расстояния в эвольвентном зацеплении его передаточное отношение не изменяется. Т.е. эвольвентное зацепление имеет малую чувствительность к погрешностям монтажа передачи (небольшим погрешностям).

т.е.

Свойство 3. При изменении межосевого расстояния в эвольвентном зацеплении величина произведения межосевого расстояния на косинус угла зацепления не изменяется.

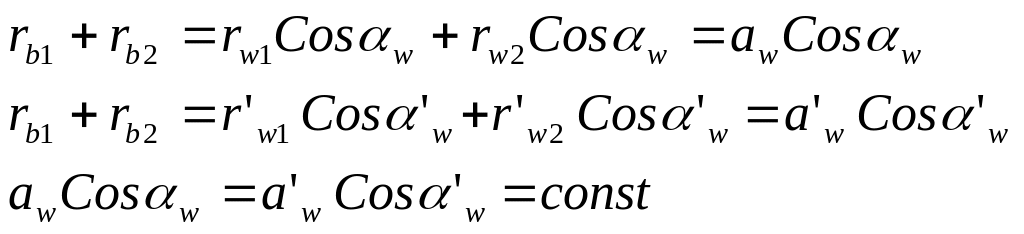
Свойство 4. За пределами отрезка линии зацепления рассматриваемые ветви эвольвент не имеют общей нормали, т. е. профили, выполненные по этим кривым будут не касаться, а пересекаться. Это явление называется интерференцией эвольвент или заклиниванием.

Эвольвентное зубчатое колесо и его параметры. Параметры эвольвентного зубчатого колеса

Существует три параметра зубчатого колеса, которые можно определить «на глаз» при наличии этого зубчатого колеса и 2 которые можно только рассчитать.

1. Число зубьев колеса , можно подсчитать по готовому колесу (при проектировании этим параметром задаются).

2. Окружность вершин, окружность впадин . При наличии колеса могут быть измерены, например, штангенциркулем. Окружность вершин – это окружность, ограничивающая зуб со стороны противоположной телу колеса. Окружность впадин – это окружность, ограничивающая зуб со стороны тела колеса. Зная эти окружности можно получить высоту зуба колеса: .

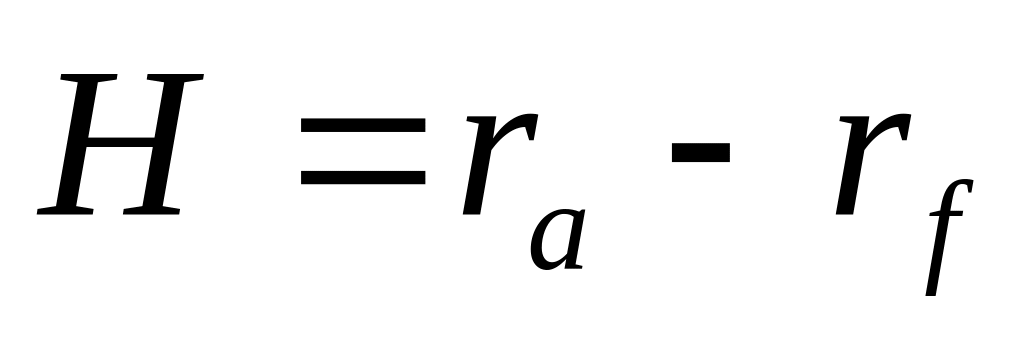3. Для получения эвольвентного профиля необходимо знать расположение основной окружности колеса - рассчитывается.

4. Делительная окружность – делит зуб на ножку зуба и головку зуба. Делительной окружностью называется окружность стандартного шага, модуля и угла давления (или окружность, проходящая через точку эвольвенты для которой профильный угол ).

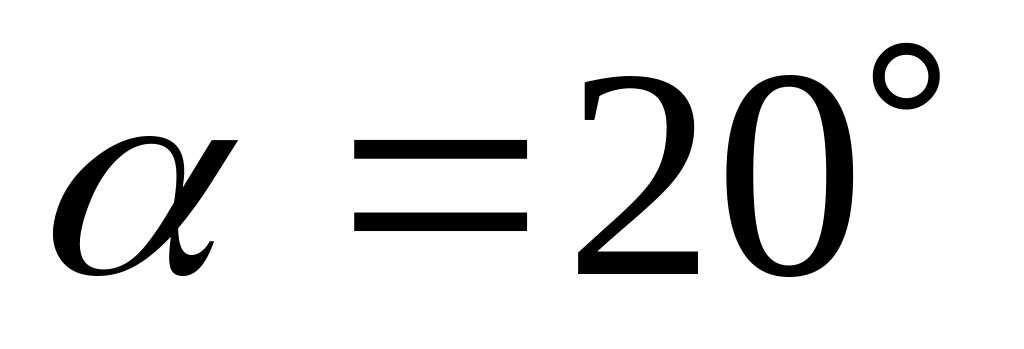5. Модулем зацепления называется линейная величина в  раз меньшая окружного шага или отношение шага по любой концентрической окружности зубчатого колеса к . В зависимости от окружности, по которой определен модуль, различают делительный, основной, начальный. Для косозубых колес еще и нормальный, торцевой и осевой модули. В ряде стран используется величина обратная модулю, которая называется питчем. Питч (диаметральный) - число зубьев колеса, приходящееся на дюйм диаметра. Исходя из этого, модуль можно определить как число миллиметров диаметра, приходящееся на один зуб. На колесе можно провести бесчисленное число окружностей, на каждой из которых будет свой модуль. Для ограничения этого числа ГОСТом введен стандартный ряд модулей. Стандартной модуль определяется по делительной окружности .

6. Окружным шагом, или шагом, называется расстояние между одноименными точками профилей двух соседних зубьев, измеренное по дуге любой окружности (под одноименными понимаются правые или левые профили зуба). Обозначается . Достаточно часто вводится понятие углового шага 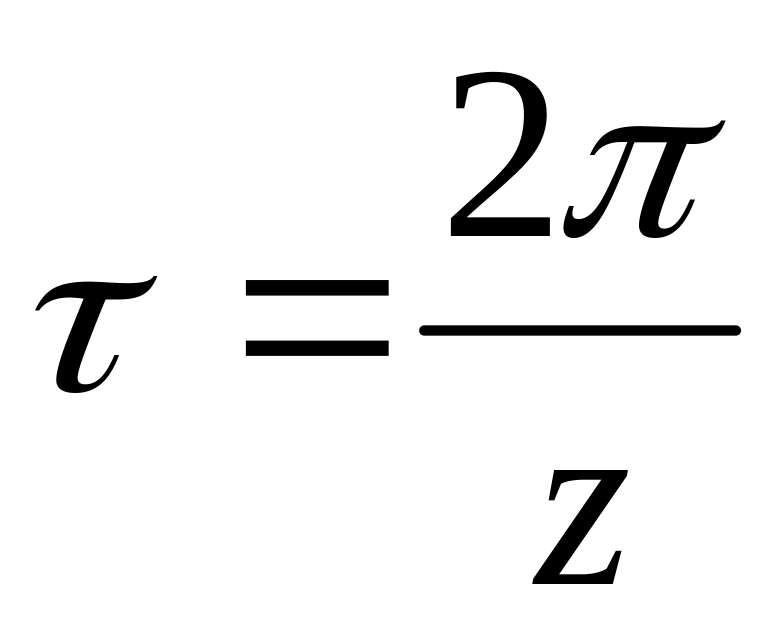- центральный угол, соответствующий дуге окружного шага по делительной окружности. Шаг колеса делится на толщину зуба 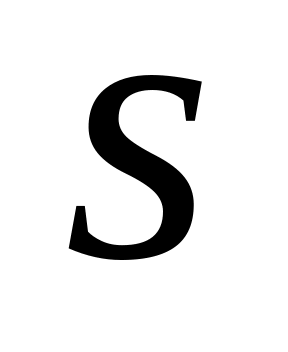и ширину впадины 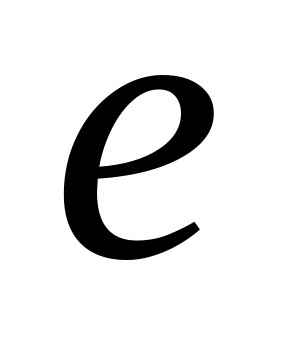: 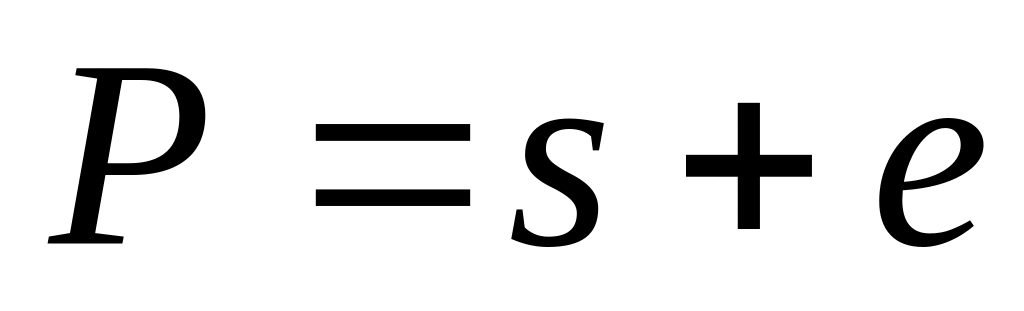. Толщина зуба - расстояние по дуге соответствующей окружности между разноименными точками профилей зуба. Ширина впадины - расстояние по дуге соответствующей окружности между разноименными точками профилей соседних зубьев.

7. - угловая толщина зуба. 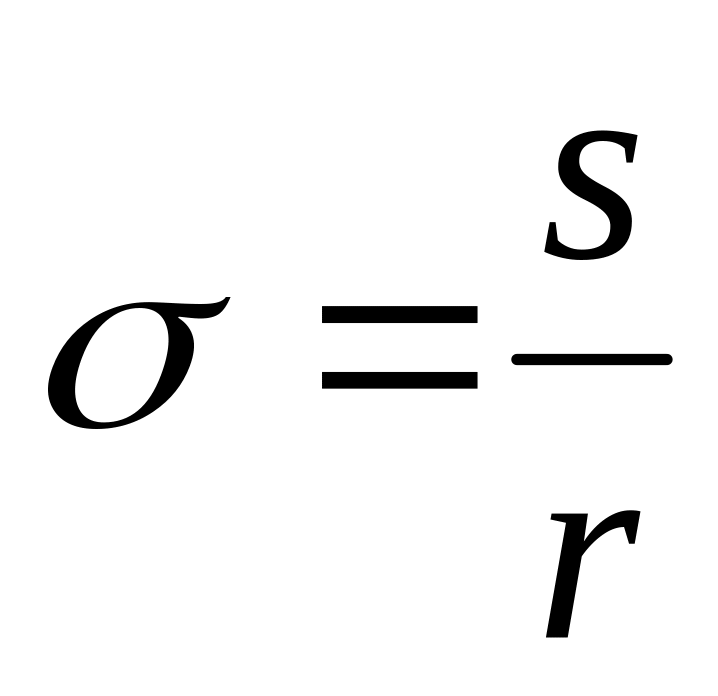- центральный угол соответствующий дуге .

8. - окружность произвольного радиуса.