10. Необходимые и достаточные условия минимума (максимума) функции многих переменных. Классический метод

Теорема Ферма (необходимое условие оптимальности): Пусть функция f(x,y) определена и дифференцируема на R2 , и в точке (x*, y*) достигает экстремума (min или max), тогда все частные производные первого порядка данной функции в этой точке должны быть равны нулю.

двух переменных.

Необходимые условия существования экстремума.

Пусть 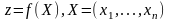, т.е. . При этом предполагается, что 1-я и 2-я частные производные f(x) непрерывны в каждой точке Х.

Приведем другую формулировку теоремы Ферма.

Теорема 1:

Если точка является экстремальной точкой функции f(x), то grad .

Данное условие удовлетворяется в точках перегиба и седловых точках функции.

Точки, удовлетворяющие уравнению grad f(X₀) = 0 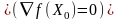будем называть стационарными.

3.5. Достаточные условия существования экстремума.

Определение 2. Если вычислить еще раз производные по соответствующим переменным от вектора, состоящего из частных производных (градиента функции), то получим матрицу вторых производных (иногда называемую матрицей Гессе)

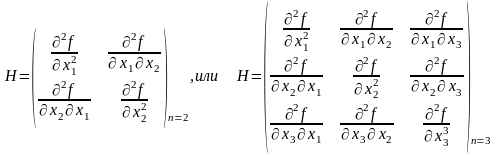
Теорема 2:

Стационарная точка Х₀ является экстремальной, когда матрица Гессе Н в точке Х₀ оказывается

положительно определенной (тогда Х₀ – точка min);

отрицательно определенной (тогда Х₀ – точка max).

Пример 1. Рассмотрим функцию

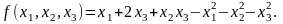
Найдем ее стационарные точки

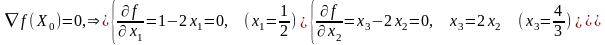
Проверим выполнение достаточного условия

Главные миноры равны: -2; 4; -6  - отрицательно определенная матрица  - точка max. Если бы - являлась неопределенной матрицей, то Х₀ – являлась бы седловой точкой.

Пример 2. Рассмотрим функцию трех переменных

f(x1,x2,x3) = 0,5<AX, X> + <b, X>

где матрица А и вектор b заданы следующим образом:

A = , b = ,

Тогда

f(x₁, x₂, x₃) = =

= =

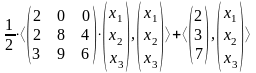= 0,5(2x₁² + 2x₁x₂ + 8x₂² +4x₂x₃ + 3x₁x₃ + 9x₂x₃ + 9x₃²) +

+ 2x₁ + 3x₂ + 7x₃ =

= x₁² + x₁x₂ +4x₂² + 6,5x₂x₃ + 1,5x₁x₃ +3x₃² + 2x₁ + 3x₂ + 7x₃ .

Найдем стационарные точки рассматриваемой функции. Для этого нужно вычислить частные производные по каждой переменной и приравнять нулю.

.

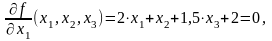
Сведем систему из трех уравнений к системе двух уравнений. Для этого умножим второе уравнение на 2 и из полученного уравнения вычтем первое уравнение. Получим

15x₂ + 11,5x₃ + 6 = 0.

Далее, умножим первое уравнение на 3, а третье уравнение на 4, и из последнего уравнения вычтем предыдущее. Получим

23x₂ + 19,5x₃ + 22 = 0.

Решая полученную систему двух уравнений методом исключения относительно x₂ и x₃, получим x₂ =6,25 и x₃ =-8,5.

Добавив первое уравнение, имеем

2x₁ +x₂ + 1,5x₃ +2 = 0,

x₂ = 6,25,

x₃ = -8,5.

Выразим первую переменную x₁ через остальные, получим

x₁ = (- x₂ – 1,5x₃ -2)/2,

x₂ = 6,25,

x₃ = -8,5.

Подставим значения x₂ и x₃ в первое уравнение и получим

x₁ = [-6,25-1,5(-8,5)-2]/2,

x₂ = 6,25,

x₃ = -8,5.

В результате получим,

x₁ = 2,25,

x₂ = 6,25,

x₃ = -8,5.

Значит, 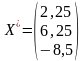- стационарная точка, в которой возможен экстремум.

Согласно теореме 2 вычисляем матрицу Гессе:

Т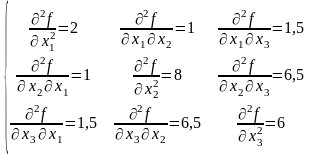 ак как

Получим

₁ = 2>0,

₂ = 28 11 =15>0,

₃ =286 + 16,51,5 + 16,51,5 – 1,581,5 – 6,56,52 – 116 = 7>0.

Значит, H  положительно определенная матрица. Стало быть, стационарная точка является точкой минимума.