8. Необходимое и достаточное условие положительной(отрицательной) определенности

Определение 4.

Квадратичная форма называется:

1. положительно определенной, если L(X)>0 для всех X0;

2. положительно полуопределенной, если L(X)0, для X и  X0 такое, что L(X)=0.

3. отрицательно определенной, если (–L(X)) есть положительно определенная квадратичная форма;

4. отрицательно полуопределенной, если (–L(X)) – положительно полуопределенная квадратичная форма;

5. неопределенной – в остальных случаях.

Теорема 5 (Необходимые и достаточные условия положительной (отрицательной) определенности квадратичной формы):

1. Квадратичная форма L(X) является положительно определенной , когда значения всех угловых главных миноров матрицы А положительны (матрица А – называется положительно определенной матрицей).

2. Квадратичная форма L(X) является отрицательно определенной , когда значение к-го углового главного минора матрицы А имеет знак (А–отрицательно определенная матрица).

3. Квадратичная форма L(X) является положительно полуопределенной , когда А – вырожденная матрица и все ее главные миноры неотрицательны (А – положительно полуопределенная матрица).

9. частные производные функции многих переменных. Понятие о градиенте функций многих переменных

Определение частных производных функции многих переменных. Понятие градиента.

Чтобы избежать громоздких обозначений, ограничимся здесь функциями трех переменных. Случай большего числа переменных полностью аналогичен.

Итак, пусть числовая функция u =f(х, y, z) определена в некоторой открытой области D. Возьмем некоторую точку М(а, b, с) из этой области. Если значения переменных у, z оставить равными b, с соответственно, а х изменять, то и будет фактически функцией одной переменной х (по крайней мере, в некоторой окрестности точки b); поэтому можно поставить вопрос о наличии производной этой функции в точке а. Придадим х приращение х, тогда функция получит приращение u =f(a + х, b, с)  f(a, b, с), которое называется частным приращением по х, поскольку оно вызвано изменением значения лишь одной переменной. По определению производной, она представляет собой предел

.

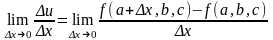Эта производная называется частной производной функции f(х, у, z) по х в точке (а, b, с). Частную производную обозначают u/х или u'_х или f '(a, b, с).

Аналогично, считая х, z равными а, с соответственно и изменяя у, можно рассматривать предел

,

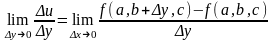который называется частной производной функции f(x, y, z) по у в точке (а, b, с) и обозначается u/y или u'_y или f '_y (a, b, с). Точно так же определяется частная производная функции f(х, у, z) по z в точке (а, b, с); она обозначается u/z или u'_z или f '_z(a, b, с). Само же вычисление частной производной по существу не представляет ничего нового по сравнению с вычислением обычной производной. Просто при вычислении частной производной по какой-то переменной все остальные считаются константами.

Пример 1. Найдем частные производные функции u =х²у + 2z. Имеем: u/х = 2ху; u/у = х²; u/z = 2.

Если собрать все частные производные, то получим трехмерный вектор (u/х, u/у, u/z). Он обозначается обычно u и называется градиентом. Градиент указывает направление наискорейшего возрастания функции в окрестности точки (x₁, ..., х_n). Антиградиент указывает направление наискорейшего убывания функции в окрестности точки (x₁, ..., х_n).

В общем случае функции n переменных этот вектор есть u(x₁, ..., х_n) = (u/х₁, ..., u/х_n). Если вектор-набор аргументов обозначить X = (x₁, ..., х_n), то иногда вводят обозначение du/dХ, понимая под этим вектор-градиент (u/х₁, ..., (u/х_n).