5. Функции многих переменных. Понятие о квадратичной форме. Свойства квадратичных форм

С линейными функциями многих переменных студентам пришлось иметь дело в задачах линейного программирования.

При решении различных прикладных задач часто приходится исследовать квадратичные формы [Мальцев, Кремер].

Определение 1. Квадратичной формой L(x_l,x₂,...,x_n) от п переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:

, (1)

Предполагаем, что коэффициенты квадратичной формы а_ij  действительные числа, причем а_ij = а_ji. Матрицу А всегда можно предполагать симметрической (показать это на практике). Действительно, значение L(X) не измениться, если каждый из пары коэффициентов 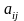и 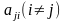заменить на 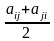. Матрица А = (а_ij) (i, j = = 1, 2, ..., n), составленная из этих коэффициентов, называется матрицей квадратичной формы.

В матричной записи квадратичная форма имеет вид:

L(X) = X'AX, (2)

где X = (x_l, х₂,..., х_n )' — матрица-столбец переменных. В самом деле

.

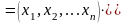
и эквивалентность формул (1) и (2) установлена.

Пример 2.1. Дана квадратичная форма L(x₁,x₂,x₃) = 2x₁² –12x₁x₂ - 10x₁x₃ +4x₂²-5x₃² . Записать ее в матричном виде.

Решение. Найдем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных, т.е. 2, 4, -5, а другие элементы  половинам соответствующих коэффициентов квадратичной формы. Поэтому

.

Выясним, как изменяется квадратичная форма при невырожденном линейном преобразовании переменных.

Пусть вектор-столбцы переменных X' = (x₁, x₂,...,x_n)' и Y'= (y₁, y₂, …., y_n)' связаны линейным преобразованием X = CY, где C=(c_ij) (i,j = 1, 2, ...,n) есть некоторая невырожденная матрица n-го порядка. Тогда квадратичная форма после применения преобразования имеет вид

L = X'AX = (CY)'A(CY) = (Y'С')A(СY) = Y'(C'AC)Y.

Итак, при невырожденном линейном преобразовании X = CY матрица квадратичной формы принимает вид:

В = С'АС. (3)

Пример 2.2. Дана квадратичная форма L(x₁,x₂) = 2x₁² –4x₁x₂ – 3x₂². Найти квадратичную форму L(у₁,y₂), полученную из данной линейным преобразованием x_l = 2у₁ - Зу₂, х₂ = у₁ + у₂

Решение. Матрица данной квадратичной формы A = ,

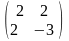а матрица линейного преобразования C =

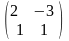
Следовательно, по (3) матрица искомой квадратичной формы

=

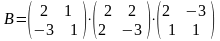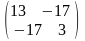
а квадратичная форма имеет вид L(y₁, у₂) = 13у₁² – 34y₁y₂ + Зу₂². Следует отметить, что при некоторых удачно выбранных линейных преобразованиях вид квадратичной формы можно существенно упростить.

Определение 2. Квадратичная форма

называется канонической (или имеет канонический или диагональный вид), если все ее коэффициенты а_ij = 0 при ij:

.

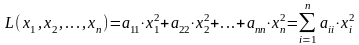а ее матрица является диагональной.

6. Приведение квадратичной формы к диагональному виду с помощью выделения полного квадрата

Теорема 1. Любая квадратичная форма с помощью невырожденного линейного преобразования переменных может быть приведена к каноническому виду.

Пример 2.3. Привести к каноническому виду квадратичную форму методом выделения полного квадрата

L(x₁,x₂,x₃) = x₁² – 3x₁x₂ + 4x₁x₃ + 2x₂x₃ +x₃²

Решение. Вначале выделим полный квадрат при переменной х₁, коэффициент при квадрате которой отличен от нуля:

L(x₁, x₂, x₃) = [x₁² – 2x₁((3·(x₂ – 4x₃)/2)+((3x₂ – 4x₃)/2)²] –

– ((3x₂ – 4x₃)/2)²+2x₂x₃ + x₃² =

= (x₁² – 3·x₂/2+ 2·x₃)² – 9·x₂²/4 + 6·x₂·x₃ – 4·x₃² + 2·x₂·x₃ + x₃² =

= (x₁² – 3·x₂/2+ 2·x₃)² – 9·x₂²/4 + 8·x₂·x₃ – 3·x₃².

Теперь выделяем полный квадрат при переменной х₂, коэффициент при которой отличен от нуля:

L(x₁, x₂, x₃) =

.

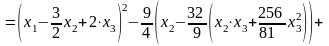
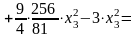
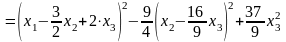'Итак, невырожденное линейное преобразование

приводит исходную квадратичную форму к каноническому виду

L(y, y₂, y₃) = y₁² – 9y₂²/4 + 37·y₃²/9.

Канонический вид квадратичной формы не является однозначно определенным, так как одна и та же квадратичная форма может быть приведена к каноническому виду многими способами, однако полученные различными способами канонические формы обладают рядом общих свойств. Одно из этих свойств формулируем в виде теоремы.

Теорема 2 (закон инерции квадратичных форм). Число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы в каноническом виде не зависит от способа приведения формы к этому виду.

Например, квадратичную форму L в примере 2.3 можно было привести к виду

L(y, y₂, y₃) = 37y₁²/4 + y₂²  y₃²,

применив невырожденное линейное преобразование

.

Как видим, число положительных и отрицательных коэффициентов (соответственно два и один) сохранилось.

Следует отметить, что ранг матрицы квадратичной формы, называемый рангом квадратичной формы, равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях.