4.2. Метод золотого сечения.

Определение 1: Функцию f(x) назовем унимодальной на отрезке [a, b], если она непрерывна на отрезке [a, b] и существуют такие числа , (a ≤  ≤ ≤ b) такие, что

1) f(x) строго монотонно убывает при a ≤ x ≤  (если a < );

2) f(x) строго монотонно возрастает при  ≤ x ≤ b (если < b);

3) f(x) = при  ≤ x ≤ , так что X* = [, ]

Случаи, когда один или два из отрезков [a, ], [, ], [, b] вырождаются в точку, здесь не исключаются.

В частности, если =, то функцию f(x) называют строго унимодальной на отрезке [a, b].

Перейдём к описанию метода минимизации унимодальной функции на отрезке, основанном на отношении золотого сечения.

Как известно, золотым сечением отрезка называется деление отрезка на две неравные части так, что отношение длины всего отрезка к длине большей части равнялось отношению длины большей части к длине меньшей части отрезка. Если взять за единицу длину всего отрезка, а за t обозначить длину большего отрезка, тогда (1-t) – будет длиной малого отрезка. Тогда это отношение (золотое сечение) находится из следующего уравнения

,

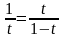Таким образом, t² + t - 1 = 0, откуда t₁ = (-1 + 5)/2 = 0,618033989. Отрицательный корень t₂ = (-1 - 5)/2 этого уравнения не подходит в качестве золотого сечения.

Легко проверить, что золотое сечение отрезка [a, b] производится двумя точками x₁ = a+(3-5)*(b-a)/2 = a+(b-a)*0,381966011 и x₂ = a+(-1+5)*(b-a)/2 = a+(b-a)*0,61803989, расположенными симметрично относительно середины отрезка, причём a<x₁<x₂<b.

В результате анализа двух рассмотренных значений функции будет определен тот интервал, который должен исследоваться в дальнейшем. Этот интервал будет содержать одну из предыдущих точек и следующую точку, помещаемую симметрично ей. Первая точка находится на расстоянии (b-a)0,381966011 от одного конца интервала, вторая — на таком же расстоянии от другого. Далее х₁ и х₂ будем обозначать через u₁ и u₂, соответственно.

Замечательно здесь то, что точка u₁ в свою очередь производит золотое сечение отрезка [а, u₂], так как u₂ - u₁ < u₁ - а = b - u₂ и (u₂ - а)/(u₁ - a) = (u₁ - а)/(u₂ – u₁). Аналогично точка u₂ производит золотое сечение отрезка [u₁, b]. Опираясь на это свойство золотого сечения, можно предложить следующий метод минимизации унимодальной функции f(u) на отрезке [a, b].

Положим a₁ = a, b₁ = b. На отрезке [а₁, b₁] возьмем точки u₁, u₂, производящие золотое сечение, и вычислим значения f(u₁), f(u₂). Далее, если f(u₁)≤f(u₂), то примем a₂= u₁, b₂ = u₂, = u₁; если же f(u₁)>f(u₂), то примем а₂=u₁, b₂ = b₁, = u₂. Поскольку функция f(u) унимодальна на [а, b], то отрезок [а₂, b₂] имеет хотя бы одну общую точку с множеством U_* точек минимума f(u) на [a, b]. Кроме того, b₂-а₂ = (5- 1) (b-а)/2 и весьма важно то, что внутри [a₂, b₂] содержится точка с вычисленным значением f( ) = min{f(u₁); f(u₂)}, которая производит золотое сечение отрезка [a₂, b₂].

Пусть уже определены точки u₁, ..., u_n-1, вычислены значения f(u₁), ..., f(u_n-1), и найден отрезок [а_n-1, b_n-1] такой, что

[а_n-1, b_n-1]U_* ≠, b_n-1-a_n-1=((5-l)/2)^n-2*(b-a), и известна точка 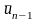, производящая золотое сечение отрезка [а_n-1, b_n-1] и такая, что f( ) = 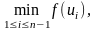(n2). Тогда в качестве следующей точки возьмем точку u_n = а_n + b_n-1 - , также производящую золотое сечение отрезка [a_n-1, b_n-1], вычислим значение f(u_n).

Пусть для определенности a_n-₁ <u_n< < b_n-1 (случай < u_n рассматривается аналогично). Если f(u_n)f( ), то полагаем a_n = a_n-1, b_n = , = u_n, если же f(u_n) >f( ), то полагаем a_n = u_n, b_n = b_n-1, = . Новый отрезок [a_n, b_n] таков, что [a_n, b_n]U_* ≠ , b_n-a_n = ((5 -1)/2)^n-1*(b-а), точка производит золотое сечение [a_n, b_n]„| и f( ) = min{f(u_n); f( )}= .

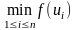Если число вычислений значений f(x) заранее не ограничено, то описанный процесс можно продолжать, например, до тех пор, пока не выполнится неравенство b_n-а_n<, гдо  — заданная точность. Если же число вычислений значений функции f(x) заранее жестко задано и равно n, то процесс на этом заканчивается и в качестве решения задачи второго типа можно принять пару (f( ), ), где f( ) является приближением для f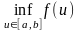_* = , а точка служит приближенном для множества U_* с некоторой погрешностью.

Алгоритм поиска точки минимума по методу золотого сечения.

Шаг 1. Полагаем k=0, a_k = a₀ = 0, b_k = b₀ = 10,  = 0,1.

Шаг 2. Полагаем _k = b_k – a_k.

Шаг 3. Если _k <, то перейти в шагу 6, иначе перейти к следующему шагу 4.

Шаг 4. Положим

u1 = a_k + (b_k - a_k)0,381966011,

u2 = a_k + (b_k - a_k)0,61803989.

Вычислим f(u1) и f(u2).

Шаг 5. Если f(u1)<f(u2), то полагаем

a_k+1 = a_k, b_k+1 = u2, а также полагаем k:=k+1 и перейдем к шагу 2,

в противном случае (иначе) полагаем

a_k+1 = u1, b_k+1 = b_k,

а также полагаем k:=k+1 и переходим к шагу 2.

Примечание 1. Отметим, что _k = b_k – a_k.= (0,61803989)^k₀.

Шаг 6. Положим f(x_*) = min{f(u1), f(u2)} и x_* = arg min{f(u1), f(u2)}.

Примечание 2. Можно показать, что в случае если f(u1)<f(u2) величина u2 на следующем (k+1)-ом шаге совпадет с u1 на данном k-ом шаге, а в противном случае наоборот величина u1 на следующем (k+1)-ом шаге совпадет с u2 на данном k-ом шаге. Это означает, что на каждой итерации метода золотого сечения нам достаточно вычислять одно, а не два значения f(u).