7. Положительная (отрицательная) определенность квадратичных форм. Критерий сильвестра

Определение 3. Квадратичная форма L(х₁,х₂,...,х_n) называется положительно (отрицательно) определенной, если при всех значениях переменных, из которых хотя бы одно отлично от нуля,

L(х₁,х₂,...,х_n) > 0 (L(х₁,х₂,...,х_n) < 0).

Так, например, квадратичная форма

L₁ = 3x₁² + 4x₁² + 9x₃²

является положительно определенной, а форма

L₂ = 10x₁² + 2x₁x₂  5x₂²

— отрицательно определенной.

Нарисуем трехмерный график (пространственную форму) отрицательно-определенной квадратичной формы.

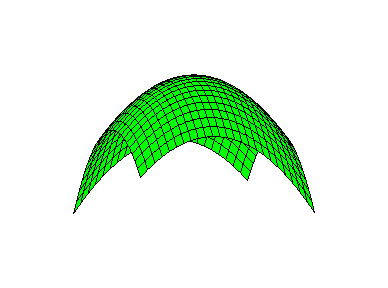
Рис.1. График отрицательно-определенной формы.

Теорема 3. Для того чтобы квадратичная форма L = Х'АХ была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения i, матрицы А были положительны (отрицательны).

В ряде случаев для установления знакоопределенности квадратичной формы удобнее бывает применить критерий Сильвестра.

Теорема 4 (критерий Сильвестра). Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы этой формы были положительны, т.е ₁> 0, ₂> 0,…, _n>0, где

.

Следует отметить, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, начиная со знака "минус" для минора первого порядка.

Доказательство. При n=1 теорема верна, так как форма имеет в этом случае вид ах² и поэтому положительно определена тогда и только тогда, если а>0. Будем поэтому доказывать теорему для случая n неизвестных, предполагая, что для квадратичных форм от n  1 неизвестных она уже доказана.

Сделаем сначала следующее замечание:

Если квадратичная форма L с действительными коэффициентами, составляющими матрицу A подвергается невырожденному линейному преобразованию с действительной матрицей Q, то знак определителя квадратичной формы (т.е. определителя ее матрицы) не меняется.

Действительно, после преобразования мы получаем квадратичную форму с матрицей Q^ТAQ, однако, ввиду |Q^Т| = |Q|,

Q^ТAQ  = Q^ТAQ=AQ²,

т. е. определитель |А| умножается на положительное число.

Пусть теперь дана квадратичная форма

Ее можно записать в виде

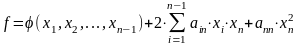, (4)

где  будет квадратичной формой от n1 неизвестных, составленной из тех членов формы L, в которые не входит неизвестное х_n.

Главные миноры формы  совпадают, очевидно, со всеми, кроме последнего, главными минорами формы L.

Необходимость. Пусть форма L положительно определена. Форма  также будет в этом случае положительно определенной: если бы существовали такие значения неизвестных х₁, х₂, …, х_n-1, не все равные нулю, при которых форма  получает не строго положительное значение, то, полагая дополнительно х_n = 0, мы получили бы, ввиду (4), также не строго положительное значение формы L, хотя не все значения неизвестных x₁, х₂, ... , x_n-1, х_n равны нулю. Поэтому, по индуктивному предположению, все главные миноры формы , т. е. все главные миноры формы L, кроме последнего, строго положительны. Что же касается последнего главного минора формы L, т. е. определителя самой матрицы А, то его положительность вытекает из следующих соображений: форма L, ввиду ее положительной определенности, невырожденным линейным преобразованием приводится к нормальному виду, состоящему из n положительных квадратов. Определитель этого нормального вида строго положителен, а поэтому ввиду сделанного выше замечания положителен и определитель самой формы L.

Достаточность. Пусть теперь строго положительны все главные миноры формы L. Отсюда вытекает положительность всех главных миноров формы , т. е., по индуктивному предположению, положительная определенность этой формы. Существует, следовательно, такое невырожденное линейное преобразование неизвестных х₁, х₂, ... , х_n-1, которое приводит форму  к виду суммы n-1 положительных квадратов от новых неизвестных у₁, у₂, ... , у_n-1. Это линейное преобразование можно дополнить до (невырожденного) линейного преобразования всех неизвестных x_l, x₂, ..., х_n, полагая х_n= у_n. Ввиду (4) форма L приводится указанным преобразованием к виду

; (5)

точные выражения коэффициентов b_in для нас несущественны. Так как

,

то невырожденное линейное преобразование

,

,

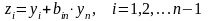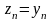приводит, ввиду (5), форму L к каноническому виду

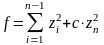. (6)

Для доказательства положительной определенности формы L остается доказать положительность числа с. Определитель формы, стоящей в правой части равенства (6), равен с. Этот определитель должен, однако, быть положительным, так как правая часть равенства (6) получена из формы L двумя невырожденными линейными преобразованиями, а определитель формы L был, как последний из главных миноров этой формы, положительным.

Доказательство теоремы закончено.

Пример 2.4. Доказать, что квадратичная форма L = 13x₁²  6x₁x₂ + 5x₂² является положительно определенной.

Решение. Первый способ. Матрица А квадратичной формы имеет вид

A =

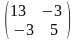
Для матрицы А характеристическое уравнение

.

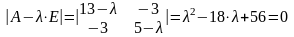Решая уравнение, найдем ₁ = 14, ₂ ⁼ 4. Так как корни характеристического уравнения матрицы А положительны, то на основании приведенной теоремы квадратичная форма L — положительно определенная.

Второй способ. Так как главные миноры матрицы А

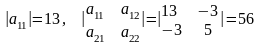
положительны, то по критерию Сильвестра данная квадратичная форма L положительно определенная.

Нарисуем трехмерный график (пространственную форму) нашей квадратичной формы L = 13x₁²  6x₁x₂ + 5x₂²

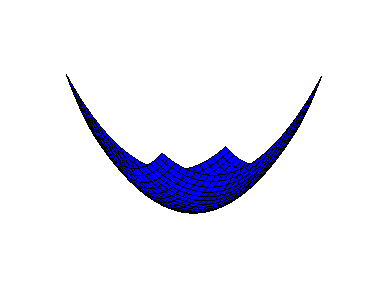
Рис.2. График положительно-определенной формы.

Таким образом, график положительно-определенной квадратичной формы имеет такой вид. Он ограничен областью определения, имеющей вид прямоугольника. На самом деле трехмерный график неограничен.