15. Методы условной минимизации. Метод проекции градиента.

Будем рассматривать задачу

f(x)→inf; xUEⁿ, (6)

где множество U необязательно совпадает со всем пространством Еⁿ, а функция f(x)C'(U). Непосредственное применение описанного выше градиентного метода в случае U≠Еⁿ может привести к затруднениям, так как точка x^k+1 из (3) при каком-то k может не принадлежать U. Однако эту трудность можно преодолеть, если полученную с помощью формулы (3) точку x^к  _kf '(x^к) при каждом к проектировать на множество U.

Определение 1. Пусть U  некоторое множество из Еⁿ. Проекцией точки x из Еⁿ называется ближайшая к х точка множества U, т.е. wU, удовлетворяющая условию

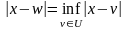
Проекцию точки х на множество U будем через Pr_U(x) =w.

В результате мы придем к так называемому методу проекции градиента.

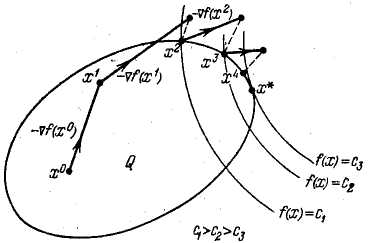
Рис. 5.1. Метод проекции градиента.

А именно, пусть x⁰U — некоторое начальное приближение. Далее будем строить последовательность {u_к} по правилу

x^к+1 = Pr_U(x^к  _kf '(x^к)), k= 0, 1, …, (7)

где _k  положительная величина. Если U — выпуклое замкнутое множество и способ выбора {_k} в (7) задан, то в силу теоремы 4.4.1 [Васильев] последовательность {x^k} будет однозначно определяться условием (7). В частности, при U = Eⁿ метод (7) превратится в градиентный метод.

Если в (7) на некоторой итерации оказалось x^k+1 = x^k (например, это случится при f '(x^k) = 0), то процесс (7) прекращают. В этом случае точка u_k удовлетворяет необходимому условию оптимальности

x^k = P_U(x^k  _kf '(x^k)),

и для выяснения того, является ли в действительности x^k решением задачи (6) или нет, при необходимости нужно провести дополнительное исследование поведения функции f(x) в окрестности точки x^k. В частности, если f(x)  выпуклая функция, то такая точка x^k является решением задачи (6).

В зависимости от способа выбора _k в (7) можно получить различные варианты метода проекции градиента. Укажем несколько наиболее употребительных на практике способов выбора _k.

1) Введем функцию одной переменной

_k() = f(Pr_U(x^k  _kf '(x^k))), (0)

и определим _k из условий

_k(_k) = 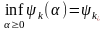, _k >0. (8)

Очевидно, при U = Eⁿ метод (7), (8) превратится в метод наискорейшего спуска. Поскольку величину _k из условий (8) удается найти точно лишь в редких случаях (возможно также, что нижняя грань в (8) не всегда достигается), то _k на практике определяют приближенно.

2) Иногда приходится довольствоваться нахождением какого-либо _k>0, обеспечивающего условие монотонности: f(x^k+l)< f(x^k). Для этого обычно выбирают какую-либо постоянную  > 0 и в методе (2) на каждой итерации берут _k = , а затем проверяют условие монотонности и при необходимости дробят величину _k = , добиваясь выполнения условия монотонности.

3) Если функция f(x) принадлежит С^1,1(U) и константа Липшица L для градиента f '(x) известна [Васильев], то в (7) в качестве _k можно взять любое число, удовлетворяющее условиям

0<₀ ≤ _k ≤ 2/(L+2), (9)

где 0,   положительные числа, являющиеся параметрами метода.

4) Возможен выбор _k из условия

f(x^k)  f(Pr_U(x^k  _kf '(x^k)))  x^k  Pr_U(x^k  _kf '(x^k )), (10)

где  > 0 — параметр метода. Для определения такого _k можно взять какое-либо число _k =  (например,  = 1) и затем дробить его до тех пор, пока не выполнится условие (10). Если f(x) принадлежит С^1,1(U), то можно показать, что выполнения условия (10) можно добиться за конечное число дроблений.

5) Возможно априорное задание величин _k из условий

_k >0, к = 0,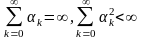1,…; , (11)

например, _k = (k+1)^-1 (k = 0, 1, ...). Сходимость метода (7), (11) была исследована в [Васильев].

Заметим, что описанные здесь варианты метода (7) при U = Еⁿ переходят в соответствующие варианты градиентного метода.

На практике для ускорения сходимости вместо (7) часто пользуются более общим вариантом метода проекции градиента

x^к+1 = x^k + _k(Pr_U(x^к  _kf '(x^к))  x^k) =

= _k Pr_U(x^к  _kf '(x^к)) + (1  k)x^k, 0<k ≤ 1, _k >0, (7')

где параметры _k и _k могут выбираться различными способами.

Заметим, что в методах (7) или (7') на каждой итерации, кроме выбора параметров _k и _k, нужно еще проектировать точку на множество U или, иначе говоря, решить задачу минимизации

F_k(x) = x  (x^k  _k f '(x^к))²  inf, xU; (12);

здесь возможно использование функции

F_k(x) = x  x^k² + 2_k<f '(x^к), x x^k>,

отличающейся от предыдущей функции постоянным слагаемым. Задачу (12) можно решать приближенно и вместо точки x^k+1U, F_k(x^k+1) = 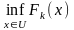= F_k*, определить ее приближение z^k+1 из условий

z^k+1U, F_k(z^k+1) ≤ F_k* + _k². (13)

Конечно, задачи (12), (13) далеко не всегда просто решаются. Поэтому методом проекции градиента обычно пользуются лишь в тех случаях, когда проекция точки на множество легко определяется. Например, когда множество U представляет собой шар в Еⁿ, параллелепипед, гиперплоскость, полупространство или положительный октант, задача проектирования точки решается просто и в явном виде, и реализация каждой итерации метода проекции градиента в этом случае не вызывает особых затруднений. Если же задача проектирования для своего решения в свою очередь требует применения тех или иных итерационных методов, то эффективность метода проекции градиента, вообще говоря, значительно снижается.

Алгоритм метода проекции градиента.

Будем считать, что некоторая начальная точка x⁰ выбрана так, чтобы выполнялись условия теоремы Вейерштрасса, а именно множество С(x⁰) = {xRⁿ  f(x)  f(x⁰)} было замкнуто и ограничено.

Шаг 1. Полагаем k=0 (номер итерации), x^k = x⁰ = 0,  = 0,01.

Шаг 2. Вычисляем h(x^k) = f '(x^k), а также _k = |x^k  x^k-1 |.

Шаг 3. Если _k <, то перейти в шагу 6, иначе перейти к следующему шагу 4.

Шаг 4. Вычислим _k>0 из условия.

Введем функцию одной переменной

_k() = f(Pr_U(x^k  _kf '(x^k))), (0)

и определим _k из условий

_k(_k) = , _k >0

Шаг 5. Вычисляем следующее приближение

x^k+1 = Pr_U(x^k  _kf '(x^k)).

Полагаем k:= k+1 и переходим к шагу 2.

Шаг 6. В качестве точки минимума возьмем последнее приближение

x_* = x^k,

а также в качестве минимального значения функции f(x_*) = f(x^k).