17. Система линейных однородных уравнений для вычисления собственных векторов

6.2. Основные определения.

Центральную роль при изучении квадратных (nxn) – матриц А играют те специальные вектора из Rⁿ, направления которых не меняются (за исключением возможно знака), при умножении на А. Всякий такой ненулевой вектор u должен удовлетворять равенствам

(1)

для некоторого скаляра , называемого собственным значением матрицы А. Каждый ненулевой вектор, кратный вектору называется собственным вектором, и  и u соответствуют друг другу. По соглашению нулевой вектор не может быть собственным вектором.

Собственные числа  должны удовлетворять системе однородных линейных алгебраических уравнений

Согласно теории линейных алгебраических уравнений, однородная система уравнений имеет ненулевое (нетривиальное) решение тогда, и только тогда, когда определитель матрицы этой системы равен нулю, т.е.

(2)

Поэтому А может иметь не более n собственных значений. Множество этих значений на комплексной плоскости составляет спектр матрицы А.

18. Характеристическое уравнение

Согласно теории линейных алгебраических уравнений, однородная система уравнений имеет ненулевое (нетривиальное) решение тогда, и только тогда, когда определитель матрицы этой системы равен нулю, т.е.

(2)

Поэтому А может иметь не более n собственных значений. Множество этих значений на комплексной плоскости составляет спектр матрицы А

Уравнение (2) называется характеристическим уравнением матрицы А, а его корни – характеристическими числами или собственными значениями матрицы А. Многочлен n-ой степени, стоящий в левой части уравнения (2) называется характеристическим многочленом матрицы А.

Пример 1. Найти собственные значения и собственные векторы линейного оператора , заданного матрицей А =

Решение. Составляем характеристическое уравнение

A  E = = 0

или

²  7 + 6 = 0 ,

откуда собственные значения линейного оператора , заданного матрицей А будут таковы ₁ = 1, ₂ = 6.

Находим собственный вектор x⁽¹⁾ =(x_l, x₂), соответствующий собственному значению ₁ = 1. Подставим это первое собственное число в систему уравнений (1). Получим систему однородных уравнений

2x₁+2x₂ = 0;

3x₁+3x₂ = 0,

откуда находим х₂ = -х₁. Положив х₁ = с, получим, что векторы х⁽¹⁾ = (с; -с) при любом с ≠ 0 являются собственными векторами линейного оператора с собственным значением ₁ = 1.

Аналогично можно убедиться в том, что векторы х⁽²⁾ = (2c_l/3, c_l).

при любом с_l ≠ 0 являются собственными векторами линейного оператора с собственным значением ₂ = 6 .

Наиболее простой вид принимает матрица А линейного оператора , имеющего n линейно независимых собственных векторов e₁, e₂, ..., e_n с собственными значениями, соответственно равными ₁, ₂, ..., _n. Векторы e₁, e₂, ..., e_n примем за базисные.

Тогда

(e_i) = _iе_i, (i = 1, 2, ..., n)

или с учетом (1)

(е_i) = а_1iе₁ + a_2ie₂ +...+a_nie_n =  _i ei

откуда a_ij = 0, если i ≠ j, и а_ii = _i, если i = j.

Таким образом, матрица оператора в базисе, состоящем из его собственных векторов, является диагональной и имеет вид:

A = .

Верно и обратное: если матрица А линейного оператора в некотором базисе является диагональной, то все векторы этого базиса — собственные векторы оператора .

Можно доказать, что если линейный оператор имеет n попарно различных собственных значений, то отвечающие им собственные векторы линейно независимы, и матрица этого оператора в соответствующем базисе имеет диагональный вид.

Пример 2. Привести матрицу А = линейного оператора к диагональному виду.

Решение. В примере 1 были найдены собственные значения матрицы ₁ = 1, ₂ = 6 и соответствующие им собственные векторы x⁽¹⁾ = (с; -с) и х⁽²⁾ = (2с₁/3; с₁) . Так как координаты векторов x⁽¹⁾ и х⁽²⁾ не пропорциональны, то векторы х⁽¹⁾ и x⁽²⁾ линейно независимы. Поэтому в базисе, состоящем из любых пар собственных векторов x⁽¹⁾=(с; -с) и х⁽²⁾ = (2с₁/3; с₁) (т.е. при любых с  0, c₁  0, например, при с = 1, с1 = 3 из векторов х⁽¹⁾ = (1; -1) и х⁽²⁾ = (2; 3) и т.д.) матрица А будет иметь диагональный вид:

A^* =  =

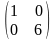
Это легко проверить, взяв, например, в качестве нового базиса линейно независимые собственные векторы х⁽¹⁾ = (1; -1) и х⁽²⁾= (2; 3). Действительно, матрица С перехода от старого базиса к новому в этом случае будет иметь вид

C = (х⁽¹⁾, х⁽²⁾) = .

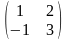Тогда в соответствии с (3.22) матрица А в новом базисе х⁽¹⁾, х⁽²⁾ примет вид:

A^* = C^-1AC = .

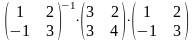Задание к лабораторной работе №7 по теме «Алгебраическая проблема собственных значений линейного оператора».

Требуется привести к диагональному виду матрицу линейного преобразования

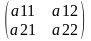
А = из своего варианта из задания №1.

Необходимо вычислить собственные значения и собственные вектора для этой матрицы. А также вычислить диагональную матрицу

A^* = B^-1AB,

где В матрица, состоящая из собственных векторов матрицы А.