18. Теоремы гергошина

Для оценки границ собственных чисел могут быть использованы следующие теоремы.

Первая теорема Гершгорина. Все собственные значения комплексной матрицы А принадлежат объединению кругов

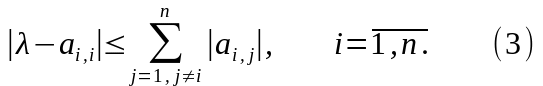
Вторая теорема Гершгорина. Если указанное в первой теореме объединение кругов распадается на несколько составных частей, то каждая такая часть содержит столько собственных значений, сколько кругов её составляют.

Пример 1: Доказать, что у матрицы В

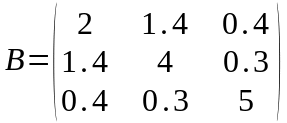
все собственные значения вещественны. Указать интервалы, которым принадлежат собственные значения.

18. Утверждение о базисе, состоящим из собственных векторов

Утверждение 1: Показать, что все собственные значения симметричной матрицы действительны.

Утверждение 2: Характеристический многочлен матрицы преобразования не зависит от выбора базиса.

Утверждение 3: Если собственные векторы u₁, u₂, ..., u_n соответствуют попарно различным собственным значениям, то они линейно независимы.

Утверждение 4: Матрица линейного преобразования А в базисе е₁, е₂, ..., е_n имеет диагональный вид тогда и только тогда, когда все векторы базиса являются собственными векторами матрицы А.

18. Приведение матрицы к диагональному виду с помощью матрицу с собственными векторами

Таким образом, матрица оператора в базисе, состоящем из его собственных векторов, является диагональной и имеет вид:

A = .

Верно и обратное: если матрица А линейного оператора в некотором базисе является диагональной, то все векторы этого базиса — собственные векторы оператора .

Можно доказать, что если линейный оператор имеет n попарно различных собственных значений, то отвечающие им собственные векторы линейно независимы, и матрица этого оператора в соответствующем базисе имеет диагональный вид.

Пример 2. Привести матрицу А = линейного оператора к диагональному виду.

Решение. В примере 1 были найдены собственные значения матрицы ₁ = 1, ₂ = 6 и соответствующие им собственные векторы x⁽¹⁾ = (с; -с) и х⁽²⁾ = (2с₁/3; с₁) . Так как координаты векторов x⁽¹⁾ и х⁽²⁾ не пропорциональны, то векторы х⁽¹⁾ и x⁽²⁾ линейно независимы. Поэтому в базисе, состоящем из любых пар собственных векторов x⁽¹⁾=(с; -с) и х⁽²⁾ = (2с₁/3; с₁) (т.е. при любых с  0, c₁  0, например, при с = 1, с1 = 3 из векторов х⁽¹⁾ = (1; -1) и х⁽²⁾ = (2; 3) и т.д.) матрица А будет иметь диагональный вид:

A^* =  =

Это легко проверить, взяв, например, в качестве нового базиса линейно независимые собственные векторы х⁽¹⁾ = (1; -1) и х⁽²⁾= (2; 3). Действительно, матрица С перехода от старого базиса к новому в этом случае будет иметь вид

C = (х⁽¹⁾, х⁽²⁾) = .

Тогда в соответствии с (3.22) матрица А в новом базисе х⁽¹⁾, х⁽²⁾ примет вид:

A^* = C^-1AC = .

Задание к лабораторной работе №7 по теме «Алгебраическая проблема собственных значений линейного оператора».

Требуется привести к диагональному виду матрицу линейного преобразования

А = из своего варианта из задания №1.

Необходимо вычислить собственные значения и собственные вектора для этой матрицы. А также вычислить диагональную матрицу

A^* = B^-1AB,

где В матрица, состоящая из собственных векторов матрицы А.

18. Модель и метод динамического программирования. Уравнение бехамана

Метод динамического программирования был разработан Ричардом Беллманом в начале 50-х годов для решения задач управления запасами. В последующие годы использовался для решения разнообразных экономических задач.

Идея метода динамического программирования состоит в том, что процесс решения исходной задачи рассматривается как многошаговый процесс, при котором конкретная задача погружается в семейство подобных ей задач - одношаговой, многошаговой и т.д. Исходная задача должна иметь последовательный характер.

Дадим общее описание модели динамического программирования (ДП).

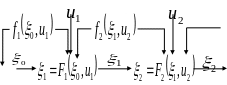
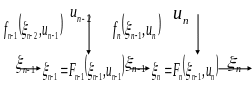Рис. 7.1. Модель задачи динамического программирования.

Поскольку в экономических задачах всегда существует время, то большинство из них должно решаться методом динамического программирования.

Рассматривается управляемая система, которая под влиянием управления переходит из начального состояния 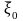в конечное состояние 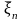. Предположим, что процесс управления системой можно разбить на n шагов. Пусть , ,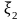…, - состояния системы после первого, второго,…, n-го шага.

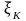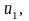
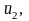Состояние системы после k-го шага характеризуется параметрами , которые называются фазовыми координатами. Состояние можно изобразить точкой s-мерного пространства, называемого фазовым пространством. Последовательное преобразование системы (по шагам) достигается с помощью некоторых мероприятий …, , которые составляют управление системой

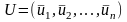
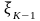где - управление на к-ом шаге, переводящее систему из состояния в состояние . Управление на к-ом шаге заключается в выборе значений определённых управляющих переменных , …, .

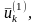
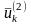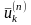Предполагаем впредь, что состояние системы в конце к-го шага зависит только от предшествующего состояния системы и управления на данном шаге. Такое свойство получило название отсутствие последействия. Обозначим эту зависимость в виде

= F_k (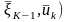 , (1.1)

Равенства (1.1) получили название уравнений состояний. Функции F_k( полагаем заданными. Варьируя управление U, получим “эффективность” процесса, которую будем оценивать количественно целевой функцией Z, зависящей от начального состояния и от выбранного управления U:

Z = Ф( ,U). (1.2)

Показатель эффективности к-го шага процесса управления, который зависит от состояния в начале этого шага и управления , выбранного на этом шаге, обозначим через f_k( (рис.1.). В рассматриваемой задаче пошаговой оптимизации целевая функция (1.2) должна быть аддитивной, т.е.

Z = 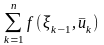. (1.3)

Если свойство аддитивности целевой функции Z не выполняется, то этого иногда можно добиться некоторыми преобразованиями функции.

Обычно условиями процесса на управление на каждом шаге накладываются некоторые ограничения. Управления, удовлетворяющие этим ограничениям, называются допустимыми.

Задачу пошаговой оптимизации можно сформулировать так: определить совокупность допустимых управлений ,…, , переводящих систему из начального состояния в конечное состояние и максимизирующих или минимизирующих показатель эффективности (1.3).

Начальное состояние и конечное состояние могут быть заданы однозначно или могут быть указаны множество ₀ начальных состояний и множество _n конечных состояний так, что ₀ , и _n. В последнем случае, в задаче пошаговой оптимизации требуется определить совокупность допустимых управлений, переводящих систему из начального состояния ₀ в конечное состояние _n и максимизирующих целевую функцию (1.3). Управление, при котором достигается максимум целевой функции (1.3), называется оптимальным управлением и обозначается через .

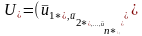Если переменные управления принимают дискретные значения, то модель ДП называется дискретной. Если же указанные переменные изменяются непрерывно, то модель ДП называется непрерывной. В зависимости от числа параметров состояний s и числа управляющих переменных r на каждом шаге различают одномерные и многомерные модели ДП.

Динамическое программирование применяется при оптимизации как детерминированных, так и стохастических процессов.

В некоторых задачах, решаемых методом ДП, процесс управления естественно разбивается на шаги. Например, при распределении на несколько лет ресурсов деятельности предприятия шагом естественно считать временной период; при распределении средств между n предприятиями номером шага естественно считать номер очередного предприятия. В других задачах разбиение на шаги вводится искусственно. Например, непрерывный управляемый процесс можно рассматривать как дискретный, условно разбив его на некоторые временные отрезки - шаги. Исходя из условий каждой конкретной задачи, длину шага выбирают таким образом, чтобы на каждом шаге получить простую задачу оптимизации и обеспечить требуемую точность вычислений.