7.2. Принцип оптимальности и уравнения Беллмана.

Принцип оптимальности.

Впервые был сформулирован Р. Беллманом в 1953 г. Метод динамического программирования состоит в том, что оптимальное управление строится постепенно, шаг за шагом.

При анализе оптимального решения подобного рода задач, разработчиками был сформулирован принцип Беллмана, который гласит:

“… Оптимальное управление должно обладать таким свойством, что каково бы ни было начальное состояние на любом шаге, и управление, выбранное на этом шаге, последующие управления должны выбираться оптимальными относительно состояния, к которому придёт система в конце данного шага”.

Вторая формулировка.

Каково бы ни было состояние  системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный.

Данная формулировка принадлежит Е.С. Вентцель и, как видно, отличается от предложенной Беллманом. Он чётко сформулировал и условия, при которых принцип верен. Основное требование – процесс управления должен быть без обратной связи, т.е. управление на данном шаге не должно оказывать влияния на предшествующие шаги.

Принцип оптимальности утверждает, что для любого процесса без обратной связи оптимальное управление таково, что оно является оптимальным для любого подпроцесса по отношению к исходному состоянию этого подпроцесса. Поэтому решение на каждом шаге оказывается наилучшим с точки зрения управления в целом. Если изобразить геометрически оптимальную траекторию в виде ломаной линии, то любая часть этой ломаной линии будет являться оптимальной траекторией относительно начала и конца.

7.3. Уравнения р. Беллмана.

Вместо исходной задачи ДП с фиксированным числом шагов n и начальным состоянием рассмотрим последовательность задач, полагая последовательно n=1,2,… при различных  - одношаговую, двухшаговую и т.д. – используя принцип оптимальности. Обозначения в ДП несут большую информационную нагрузку, поэтому очень важно их чётко усвоить.

На каждом шаге любого состояния системы , решение u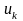 нужно выбирать осторожно, так как этот выбор влияет на последующее состояние 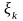и дальнейший процесс управления, зависящий от . Это следует из принципа оптимальности.

Но есть один шаг, последний, который можно для любого состояния планировать локально-оптимально, исходя только из соображений этого шага.

Рассмотрим n-ый шаг:

- состояние системы к началу n-го шага;

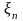-конечное состояние,

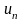– управление на n-ом шаге,

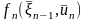-целевая функция (выигрыш) – n-го шага.

С огласно принципу оптимальности, нужно выбирать так, чтобы для любых состояний получить максимум целевой функции на этом шаге. Обозначим через - максимум целевой функции – показателя эффективности n-го шага при условии, что к началу последнего шага объект управления был в произвольном состоянии , а на последнем шаге управления было оптимальным.

называется условным максимумом целевой функции на n-ом шаге. Очевидно, что

= (5)

Максимизация ведётся по всем допустимым управлениям . Решение , при котором достигается , также зависит от и называется условно оптимальным на n-ом шаге. Оно обозначается через .

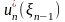Решив одномерную задачу локальной оптимизации по уравнению (5), найдём для всех возможных состояний две функции: и .

Рассмотрим теперь двухшаговую задачу: присоединим к n-му шагу (n-1)-ый шаг.

Для любых состояний 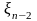, произвольных управлений 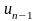, и оптимальном управлении на n-ом шаге значение целевой функции на двух последних шагах равно

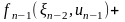(6)

Согласно принципу оптимальности для любых управление нужно выбрать так, чтобы оно вместе с оптимальным управлением на последнем n-ом шаге приводило бы к максимуму целевой функции на двух последних шагах. Следовательно, нужно найти максимум выражения (6) по всем допустимым управлениям . Максимум этой функции зависит от , обозначается через 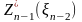, и называется условным максимумом целевой функции при оптимальном управлении на двух последних шагах. 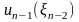Соответствующее управление на (n-1)-ом шаге обозначается через и называется условным оптимальным управлением на (n-1)-ом шаге

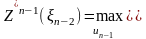(7)

Следует обратить внимание на то, что выражение, стоящее в фигурных скобках в (7), зависит только от и , так как

= ,

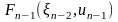и подставить вместо в функцию . В результате максимизации только по одной переменной согласно уравнению (7) вновь получаются две функции и .

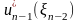Далее рассматривается трёхшаговая задача: к двум последним шагам присоединяется (n-2)-ой шаг и т.д.

Обозначим через 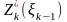условный максимум целевой функции, полученный при оптимальном управлении на n-k+1 шагах, начиная с k-го до конца, при условии, что к началу k-го шага система находилась в состоянии . Фактически эта функция равна

= .

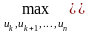Тогда

=

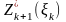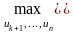
Целевая функция на последних n-k шагах при произвольном управлении на последующих n-k шагах равна

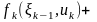
Согласно принципу оптимальности u_k выбирается из условия максимума этой суммы, т.е.

= ,

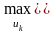k = n-1,n-2,…,2,1 (8)

Управление на k-ом шаге, при котором достигается максимум в (8), обозначается через 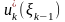и называется условным оптимальным управлением на k-ом шаге (в правую часть уравнения (8) следует подставить выражение = 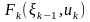, найденное из уравнений состояния).

Уравнения (8) и (7) называются уравнениями Беллмана. Это рекуррентные соотношения, позволяющие найти предыдущее значение функции, зная последующие

, ,…, , ;

, ,…, ,

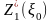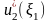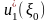
Используя эти последовательности, можно найти решение задачи ДП при данных n и , по определению - условный максимум целевой функции за n шагов при условии, что к началу 1-го шага объект управления был в состоянии , т.е.

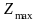= (9)

Далее следует использовать последовательность условных оптимальных управлений и уравнения состояния = . Вначале, при фиксированном получаем .

Далее, из 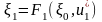находим 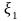и подставляем это выражение в последовательность условных оптимальных управлений и т.д. по цепочке: =  =  =  = …… =  = .

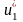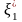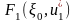
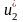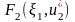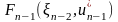
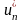18. Расчет распределения средств между двумя предприятиями

Задача 1. Планируется деятельность двух предприятий в течение n лет. Начальные средства составляют ₀. Средства х, вложенные в предприятие I, приносят к концу года доход f₁(x) и возвращаются в размере ₁(х) <х; аналогично, средства х, вложенные в предприятие II, дают доход f₂(x) и возвращаются в размере ₂(х) <х. По истечении года все оставшиеся средства заново распределяются между предприятиями I и II, новых средств не поступает, и доход в производство не вкладывается.

Требуется найти оптимальный способ распределения имеющихся средств. Будем рассматривать процесс распределения как n-шаговый, в котором номер шага соответствует номеру года. Управляемая система в данном случае это два предприятия с вложенными в них средствами. Система характеризуется одним параметром состояния 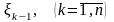- количеством средств, которые следует перераспределить в начале k-го года. Переменных управления на каждом шаге две: 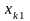и - количество средств, выделенных соответственно предприятием I и II. Так как средства ежегодно перераспределяются полностью, то .

Для каждого шага задача становится одномерной. Обозначим для краткости через , тогда .

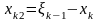Показатель эффективности k-го шага равен 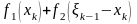- это доход, полученный от двух предприятий в течение k-го года.

Показатель эффективности задачи – доход, полученный от двух предприятий в течение n лет, составляет:

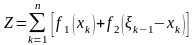. (1)

Уравнение состояния выражает остаток после k-го шага и имеет вид

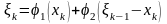. (2)

Пусть 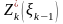- условный оптимальный доход, полученный от распределения средств между двумя предприятиями за лет, начиная с k-го года до конца n-го года.

Запишем рекуррентные соотношения для этих функций

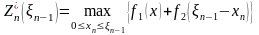(3)

,

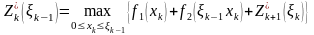где - определяется из уравнения состояния (2,6). Рассмотрим решение задачи при конкретных значениях параметров.

Задача 2. Решим задачу 1 при следующих условиях:

₀ = 10000; n = 4;

f₁(x) = 0,4x; f₂(x) = 0,3x;

₁(x) = 0,5x; ₂(x) = 0,8x;

Если x_k и (_k-1  x_k)  средства, выделенные соответственно предприятиям I и II в k-м году, то суммарный доход, получаемый в этом году от обоих предприятий равен

Z_k = 0,4x_k + 0,3(_k-1  x_k) = 0,1x_k + 0,3_k-1

а уравнения состояния (2) принимает вид

_k = 0,5x_k + 0,8(_k-1  x_k) = 0,8_k-1 – 0,3x_k,.

Основные уравнения Беллмана (3) – (4) перепишутся так

Проведем этап условной оптимизации.

4-ый шаг (k=4): Условный оптимальный доход равен

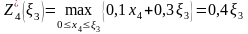
т.к. линейная относительно 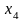функция достигает максимума в конце интервала, т.е. при .

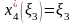3-й шаг (k=3):

.

Коэффициент при 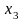- отрицателен, поэтому максимум этой линейной относительно функции достигается в начале интервала, т.е. .

3-й шаг (k=2):

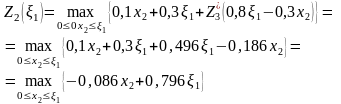
т.к. коэффициент при 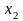- отрицателен

.

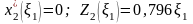1-й шаг (k=1):

.

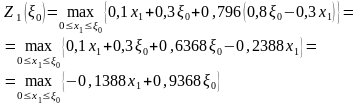Т.к. коэффициент при 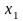- отрицателен, то

.

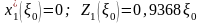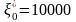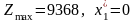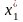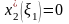Перейдем к безусловной оптимизации. Полагаем , тогда . Зная , находим . Используя , получаем и .

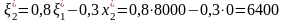Аналогично ,

.

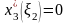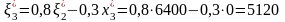Наконец .

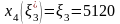Следовательно, средства по годам надо распределить так:

Предприятие	Года
	1	2	3	4
I	0	0	0	5120
II	10000	8000	6400	0

При таком распределении средств (10000 единиц) за четыре года будет получен доход, равный .

Задача 3. Решим задачу 1 при следующих условиях:

₀ =10000; n=4;

f₁(x) = 0,6x; f₂(x) = 0,5x;

₁(x) = 0,7x; ₂(x) = 0,8x.

Если x_k и (_k-1  x_k)  средства, выделенные соответственно предприятиям I и II в k-м году, то суммарный доход, получаемый в этом году от обоих предприятий равен

Z_k = 0,6x_k + 0,5(_k-1  x_k) = 0,1x_k + 0,5_k-1

а уравнения состояния (2) принимает вид

_k = 0,7x_k + 0,8(_k-1  x_k) = 0,8_k-1 – 0,1x_k,

Основные уравнения Беллмана (3) – (4) перепишутся так

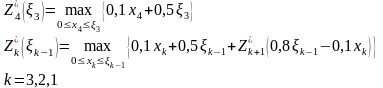
Проведем этап условной оптимизации.

4-ый шаг (k=4): Условный оптимальный доход равен

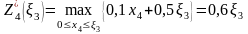
т.к. линейная относительно функция достигает максимума в конце интервала, т.е. при .

3-й шаг (k=3):

.

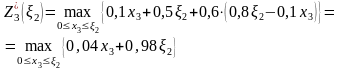Коэффициент при  положителен, поэтому максимум этой линейной относительно функции достигается в конце интервала, т.е. .

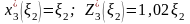3-й шаг (k=2):

т.к. коэффициент при - отрицателен .

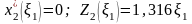1-й шаг (k=1):

.

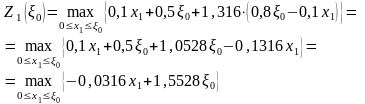Т.к. коэффициент при - отрицателен, то x₁^*(₀) = 0; Z₁^*(₀) = 1,5528₀. На этом условная оптимизация заканчивается.

Перейдем к безусловной оптимизации. Полагаем , тогда Z_max = Z₁^*(10000) = 15528, x₁^* = 0, y₁^* = ₀ = 10000, т.е. все средства выделяются второму предприятию.

Зная , находим ₁^* = 0,8₀  0,1x₁^* = 0,810000 + 0,10 = 8000. Тогда получаем x₂^* (₁) =0, y₂^* = ₁^* = 8000, т.е. все средства выделяются второму предприятию.

Используя и x₂, имеем ₂^* = 0,8₁  0,1x₂^* = 0,88000 + 0,10 = 6400.

Аналогично x₃^*(₂) = ₂^* = 6400, y₃^* = 0, т.е. все средства выделяются первому предприятию.

.

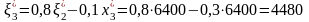Наконец 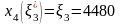, y₃^* = 0, т.е. все средства выделяются первому предприятию.

Следовательно, средства по годам надо распределить так:

Предприятие	Года
	1	2	3	4
I	0	0	6400	4480
II	10000	8000	0	0

При таком распределении средств (10000 единиц) за четыре года будет получен доход, равный Z_max = 15528.

18. Применение метода динамического программирования к задаче о замене оборудования