1Й прием.

Операции, входящие в данный прием:

- представление уменьшаемого в виде 2х слагаемых, 1е из которых = вычитаемому (теоретическая основа: табличное сложение однозначных чисел, состав числа)

- вычитание из полученной суммы 1го слагаемого, которое = вычитаемому, запись результата, которые равен 2му слагаемому (связь между компонентами действий)

1) Подготовка.

а) Состав числа в пределах 20 (табличное сложение однозначных чисел).

Реши примеры: 5+6, 7+5, 8+4, 9+8, 7+6, 8+7, 7+7, 3+9, 5+6, 8+5 и т.д.

Сравни выражения: 8+5 и 4+9; 7+7 и 5+6; 6+7 и 8+4; 9+3 и 7+6 и.т.д.

Вставь пропущенное число:

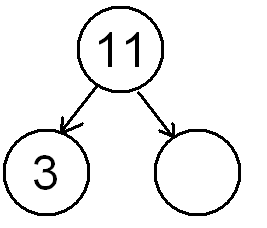
б) Связь между действиями сложения и его результатом.

Найди 1е слагаемое, если 2е слагаемое = …, а сумма = …

3+…=9

(надо рассматривать случаи сложения в пределах 10)

2) Ознакомление.

3) Закрепление.

Реши примеры с подробным комментированием.

2Й прием.

Операции, входящие в данный прием:

- вычитаем из уменьшаемого то число, которое = числу единиц в разряде единиц уменьшаемого (разрядный состав числа)

- из полученного числа 10 вычитаем оставшиеся единицы (табличное сложение чисел, состав числа)

1) Подготовка.

а) Разрядный состав двузначного числа, делая особый акцент на те упражнения, которые позволяют определить число единиц в разряде единиц двузначного числа.

Укажи число единиц 1го разряда.

Дано число 13. Чему равно число единиц в разряде единиц этого числа?

2) Ознакомление.

Для того чтобы из 12-3, вычтем из числа 12 такое число, которое равно числе единиц в разряде единиц числа 12. Таким числом является число 2. Получаем 10. Вычитаем оставшиеся единицы. Т.е. 10-1=9.

3) Закрепление:

Реши примеры с подробным комментированием.

Изучение вычислительных приемов в пределах 20 заканчивается заполнением таблицы.

Изучение табличных случаев вычитания может проходить в различной последовательности.

По Моро:

Предполагается, что сначала рассматриваются все случаи вычитания из числа 11, затем из числа 12 и т.д. до числа 18 (18-9).

2й прием – более универсальный по сравнению с 1м и имеет свое конкретное применение при изучении вычислительных приемов в дальнейшем.

11. Устные вычислительные приемы сложения в пределах 100 (3 случая подробно).

Для того, чтобы выполнять сложение и вычитание чисел в пределах 100, причем выполнять эти операции устно, в начальной школе изучаются различные приемы.

Приемов, которые изучаются для устного сложения и вычитания в концентре 100, существует достаточно много. Их изучение последовательно. Причем рекомендуется изучать сначала более легкие, потом более сложные. Уровень сложности изучаемых приемов зависит от следующих фактов:

- количество операций, входящих в изучаемый прием;

- на сколько уверенно владеют ученики теми или иными операциями, входящими в данный прием;

- от сходства или различия операций, входящих в данный прием;

- от способа моделирования приемов.

1Й случай.

40+20

Сложение круглых десятков.

Вычислительные приемы:

4дес.+2дес.=6дес.=60

ЗУН, необходимые для овладения приемом:

1) Разрядный состав числа.

2) Табличное сложение в пределах 10.