Алгебраические операции над комплексными числами.

Суммой двух комплексных чисел , является

.

При умножении

Умножение комплексных чисел легче проводить по обычным правилам раскрытия скобок с учётом, что i² = -1

Для того, чтобы разделить два комплексных числа в алгебраической форме, необходимо умножить числитель и знаменатель этой дроби на число, сопряжённое знаменателю.

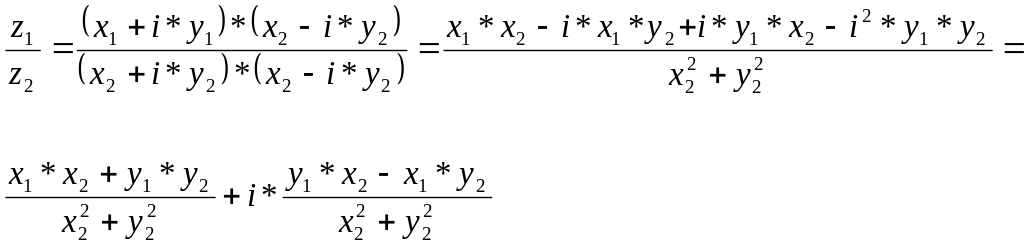
Выполним операции умножения и деления комплексных чисел в тригонометрической форме.

Пусть Z₁=q₁ (cosw₁+i*sinw₁)

Z₂=q₂ (cosw₂+i*sinw₂)

Перемножим Z₁*Z₂

Теорема: При умножении двух комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются.

Разделим два комплексных числа в тригонометрической форме.

Теорема: При делении комплексных чисел в тригонометрической форме их модули делятся, а аргументы вычитаются.

Используя правила умножения комплексных чисел в тригонометрической форме легко записать формулу Муавра для возведения комплексных чисел в n-ю степень.

Формула Муавра легко позволяет находить корни n-ой степени из комплексного числа

которое является корнем n-ой степени числа Z

При нахождении корня n-ой степени аргумент числа Z надо записывать с учетом периода

можно представить в виде

Пример: Вычислим корень 3-ей степени из 8

Представим 8 в тригонометрическом виде

Тогда

Придавая числу k различные целые значения будем получать корни 3-ей степени из 8. При этом получим только 3 различных корня

При k=0 , 2

При k=1 ,

При k=2 ,

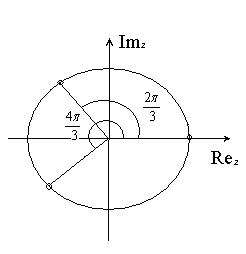
Изобразим значение корней на комплексной плоскости.

Все найденные корни обладают модулем равным 2 следовательно они находятся от начала координат на расстоянии,равном 2 единицам.

Геометрическая трактовка операций над комплексными числами.

Сложение комплексных чисел легче всего интерпретировать, используя геометрическую запись комплексного числа.

Изобразим найденное значение на координатной плоскости, сложив соответствующие координаты.

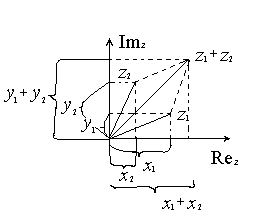
Из сделанного рисунка замечаем, что сложение комплексных чисел соответствует сложению векторов по правилу параллелограмма.

Умножение комплексных чисел иллюстрируется с помощью тригонометрической записи комплексных чисел. Пусть имеются

Изобразим полученные результаты на комплексной плоскости.

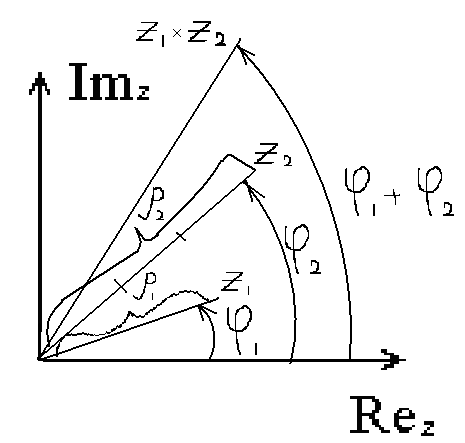
Для того, чтобы изобразить произведение двух комплексных чисел, от вектора отложим угол , затем на полученном луче откладываем от начала координат отрезок, длина которого равна произведению модулей.

Из полученного рисунка видим, что умножение комплексных чисел сводится к повороту с растяжением.

Линейные пространства

Исходя из операций над матрицами, мы ввели понятие комплексного числа. Другим важнейшим понятием, связанным с матрицами является понятие линейного пространства.

Определение: Множество L элементов , … называется линейным пространством, если выполняются следующие требования

1. На множестве L определена операция сложения элементов для = +

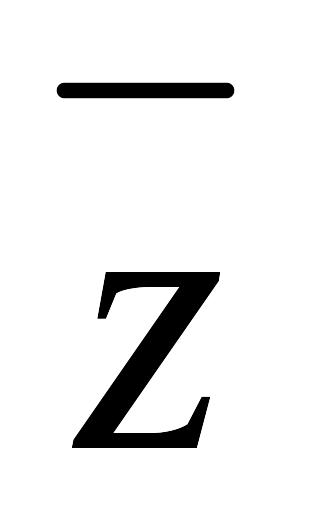
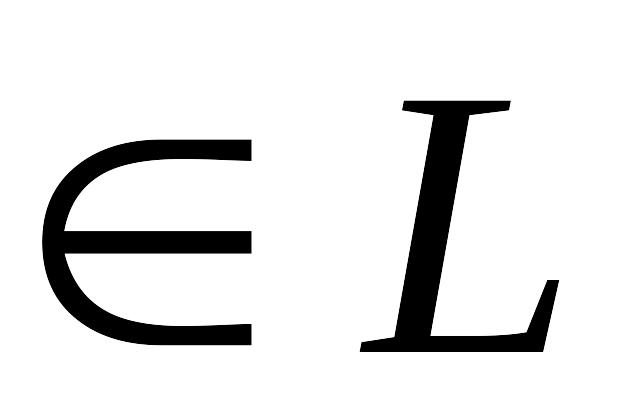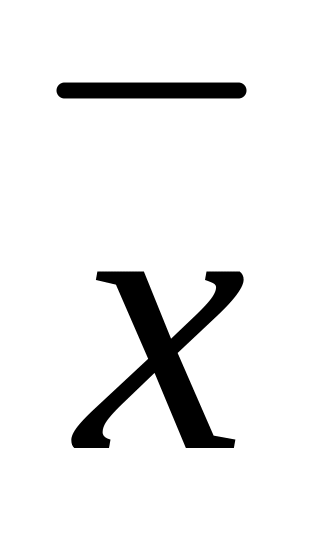2. На множестве L определена операция умножения элементов на число.Для

, называемый произведением числа на число x и обозначается

= .

3. Введенные две операции удовлетворяют следующим 8 аксиомам.

1) + = + коммутативность сложения

2) ( + ) + = + ( + ) ассоциативность сложения.

3) Существование нулевого элемента. Существует нулевой элемент такой, что для любого

= +

4) Существование противоположного элемента.

+ =

5) Для R L , ассоциативно относительно числовых множителей.

6) L ,

7) R L , дистрибутивно относительно сложения чисел .

8) R R , дистрибутивно относительно сложения элементов .

Рассмотрим множество n-мерных векторов .Напомним, что n- мерным вектором называется упорядоченная комбинация n-действительных чисел . n-мерный вектор можно рассматривать как матрицу размера 1*n . Таким образом, на множестве n-мерных векторов естественным образом вводятся операции сложения векторов и умножение вектора на число . Вводится

,

,тогда

Замечаем , что введенные операции удовлетворяют всем требованиям определения линейного пространства . Другими словами множества n- мерных векторов являются линейным пространством . Большинство линейных пространств сводится к множеству n- мерных векторов. Пусть задана совокупность k-векторов и некоторый набор вещественных чисел .Выражение называется линейной комбинацией векторов .

Пример: Пусть заданы вектора , , и вещественные числа . Вычислим линейную комбинацию заданных чисел.

Таким образом видим, что каждая линейная комбинация определяется некоторым вектором.

Пусть заданы два упорядоченных набора из n вещественных чисел

Вычислим выражения используя операции над векторами

Последнее выражение позволяет сделать вывод о замкнутости линейных комбинации векторов .Кроме того нулевой элемент можно представить , как линейную комбинацию с нулевыми коэффициентами . Таким образом множество линейных комбинаций векторов является линейным пространством, называемым линейной оболочкой векторов и обозначается < > .Говоря, что это линейное пространство V , натянуто на вектора .