Двойное векторное произведение

Определение: Выражение называется двойным векторным произведением вектором произведением векторов . Для двойного векторного произведения справедлива следующая формула:

Уравнение прямой и плоскости

Дадим определение прямой исходя из понятия линейной зависимости векторов.

Определение: Геометрическое место всех точек, каждая пара которых образует вектор коллинеарный заданному, называется прямой.

В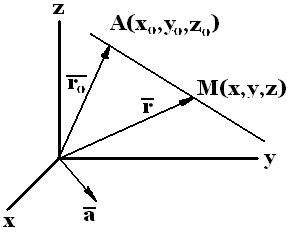 озьмем на прямой l точку A(x₀,y₀,z₀) и произвольную точку M с координатами (x, y, z). Координаты точки A определяются радиус-вектором , координаты точки M определяются радиус-вектором , при этом пара точек AM определяет вектор . Согласно определеннию прямой получаем, что колинеарен вектору , (1), где - радиус вектор начальной точки, a- направляющий вектор прямой, t – величина параметра меняя параметр t от получим всю совокупность точки прямой. При t=0 уравнение (1) определяет начальную точку A. Уравнение (1) называется векторным параметрическим уравнением прямой. Исходя из уравнения (1) всегда можно получить соответствующие скалярные уравнения для координат точек прямой

(2)

Соотношение (2) называется параметрическими уравнениями прямой. Исключая из уравнения (2) параметр t придем к каноническому уравнению прямой…

Приравняв эти значения параметра, получим:

(3)

Соотношение (3) называется каноническим уравнением прямой. Уравнения (1),(2),(3) говорят о том, что ранг матрицы RangB=1

Это означает, что миноры второго порядка:

; ;

Учитывая определение векторного произведения и выражения векторного произведения в ортогональном базисе

Равенство ранга матрицы B единицы означает, что точки прямой удовлетворяет уравнению:

(4)

Обозначим векторное произведение , (5)

Уравнение плоскости

Определение: Геометрическое место всех точек, каждая пара которых образует вектор компланарный двум заданным векторам, называется плоскостью.

З афиксируем на плоскости точку A(x₀,y₀,z₀) и определяем радиус-вектором . Возьмем произвольную точку M(x,y,z), определенную r-вектора . Вектор и он будет комплонарен векторам .

Получаем, что радиус-вектор точки M: (6), где - радиус-вектор начальной точки, - направляющие вектора плоскости t₁, t₂ – параметры. Уравнение (6) называется векторным параметрическим уравнением плоскости от вектора уравнения (6) можно всегда перейти к трем скалярным уравнениям

(7)

Уравнение (7) называется параметрическим уравнением плоскости. Соотношение (6),(7) говорят о том, что ранг матрицы менее 3. RangB<3, т.е. определитель матрицы B должен быть равен 0.

(8)

Соотношение (8) можно рассматривать как выражение смешанного произведения векторов .

Используя определение смешанного произведения выражение 8’ можно рассматривать в виде ,

где круглые скобки – скалярное произведение, квадратные скобки – векторное произведение.

Исходя из определения векторного произведения, замечаем, что векторная произведение векторов и даёт вектор в нормальный плоскости, такой что тройка векторов - правая. Таким образом уравнение 8’’ можно переписать в виде:

Обозначим скалярное произведение через некоторое число D, соотношение (9) можно переписать в виде:

(10)

Обозначим координаты нормального вектора через A,B,C

Выражение (10) можно записать в координатном виде:

Ax+By+Cz=D (11)

Уравнение (11) называется общим уравнением плоскости.