Некоторые задачи о прямых и плоскостях.

Уравнение прямой проходящей через 2 точки.

Возьмём точку А за начальную точку прямой

Вектор за направляющий вектор прямой

Используем каноническое уравнение прямой: .Получим уравнение прямой проходящей через 2 точки. Записанное уравнение прямой остаётся справедливо и в том случае, когда знаменатель какой-нибудь из дробей равен 0, в этом случае необходимо приравнять к 0 и числитель и знаменатель.

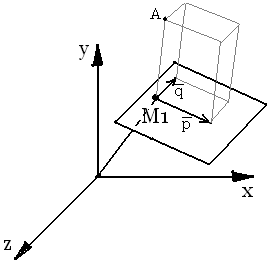
Уравнение плоскости, проходящее через три заданных числа.

Пусть на плоскости заданы 3 точки: M₁(x₁,y₁,z₁); M₂(x₁,y₁,z₁); M₃(x₁,y₁,z₁);

Выберем M₁ в качестве начальной точки плоскости. Вектора M₁M₂, M₁M₃, будем считать, как направляющие вектора плоскости, тогда уравнение плоскости может быть записано в виде:

Расстояние от точки a до плоскости.

Пусть уравнение плоскости имеет вид: Пусть плоскость задана направляющими векторами точкой M. Точка A задана радиус-вектором . Расстояние от А до плоскости проще всего определить разделив объем параллепипеда построенного на векторах на площадь его основания.

Таким образом, величина

Учитывая, что любой нормальный вектор плоскости можно представить в виде векторного произведения , . Таким образом расстояние от точки до плоскости:

Расстояние от точки до прямой.

П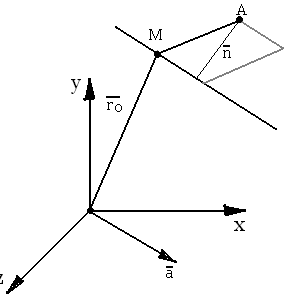 усть уравнение прямой задано в виде:

Расстояние от точки А до прямой можно определить, разделив площадь параллелограмма, построенного на векторах , на длину вектора .

То площадь: ,

и расстояние:

Расстояние между непараллельными прямыми в пространстве.

Пусть прямые в пространстве заданы векторными прямыми.

Расстояния между двумя непараллельными прямыми определяется, частным V_{параллепида}, построенного на векторах , площадь его основания .

если прямые пересекаются, то

Знаменатель ≠ 0, так как прямые непараллельные.

Кривые второго порядка

Определение: Геометрическое место точек координаты которых удовлетворяющие уравнению (1), в котором коэффициенты А,В,С не равны 0 одновременно, называются линией второго порядка.

Первые три слагаемых левой части уравнения(1) называются квадратичной формой двух переменных.

(2)

Следующие два слагаемых называют линейной формой

(3)

Каждая квадратичная форма(2) может быть с помощью перехода к новому декартовому базису приведена к следующему виду:

(2’)

при этом линейная формула(3) принимает вид

(3’)

Таким образом в новом базисе уравнения прямой (1) примет вид:

(1’)

Если величины , то квадратичная форма (1’) может быть записана

(1”)

Пример: Hрассмотрим процедуру приведения кривой второго порядка к простейшему виду, на примере уравнения:

рассмотрим квадратичную форму

запишем квадратичную форму в матричном виде

Если квадратичная форма задана в общем виде:

вычислим собственные значения

=>

Находим корни квадратного уравнения:

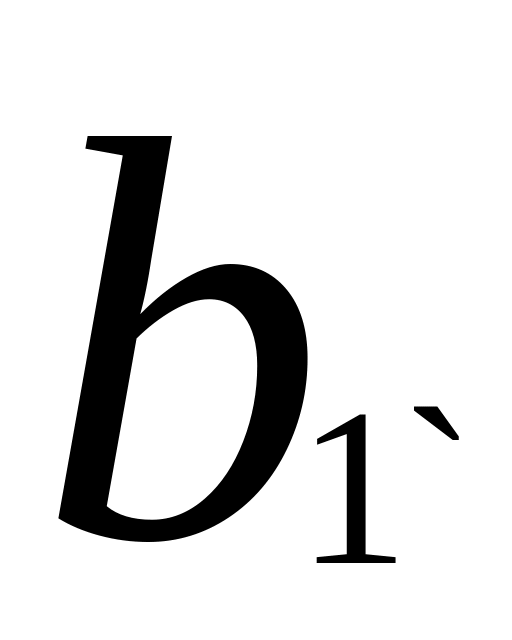
	1	2

	-2	1

Заметим, что найденные ортогональны между собой:( )

Нормируем эти вектора

= =

= =

Единичный вектор, коллинеарный будет иметь координаты:

Обозначим найденные единичные вектора в качестве нового базиса.

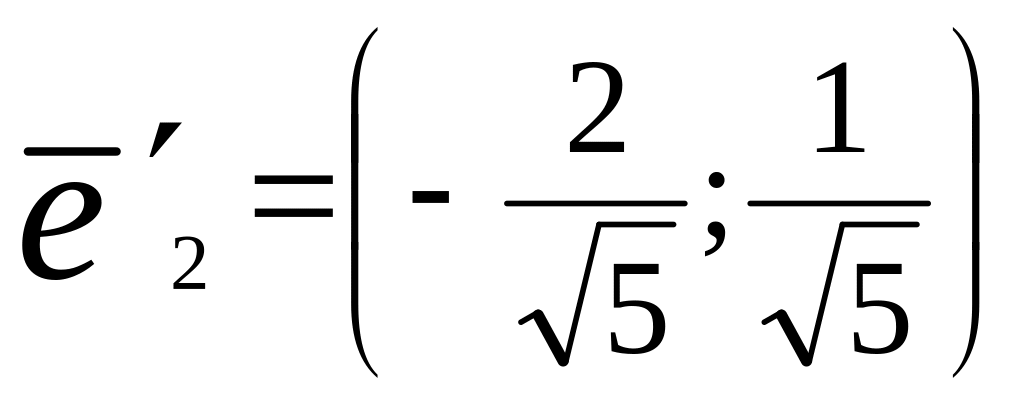
Тогда матрица перехода от старого базиса к новому будет иметь вид:

При этом старые координаты будут выражаться через новое соотношение:

Таким образом в новых координатах квадратичная форма примет вид:

Подставляя найденное выражение в соотношение для квадратичной формы, получим:

= = = =

= = =

Найдем теперь выражение для линейной формы в новом базисе:

Таким образом в новой системе координат получим:

Выделив полный квадрат по переменной x’ найдем:

=>

И окончательно находим 10X²+5Y²=10. Разделим полученное уравнение на 10, приведем его к виду:

- получили уравнение кривой.

Как ранее было показано, прямая была представлена в виде:

При этом существует такая прямоугольная система координат, в которой это уравнение принимает одно из следующих 9 канонических видов:

1) - эллипс

2) - мнимого эллипса

3) - точки

4) - гипербола

5) - пара пересекающихся прямых

6) - парабола

7) - пара параллельных прямых

8) - пара мнимых параллельных прямых, не обладают наглядным геометрической иллюстрацией

9) - прямые (пара совпадающих прямых)

В соответствии с этим существует 6 классов линий 6-го порядка.

Эллипс

Определение: Эллипсом называется линия, которая в некоторой декартовой системе координат определяется каноническим уравнением: (2)

Из уравнения (2) вытекает, что координаты точки эллипса удовлетворяют следующим условиям:

Т.е. координаты точек эллипса лежат внутри прямоугольника со сторонами 2а и2b.Точки пересечения эллипса с осями координат имеют координаты (-а;0) (а;0) (0;b) (0;-b)-эти точки называются вершинами эллипса. Переменные x,y-входят в уравнение (2)во 2-х степенях. Если точка М(x;y) лежит на эллипса, то точки с координатами (-x;y) (x;-y) (-x;-y) лежат на эллипса, отсюда следует 1-е свойство эллипса.

Каноничные оси координат являются осями симметрии эллипса, а натуральные координатным-центром симметрии.

Форму эллипса легче всего установить используя тригонометрические параметрические уравнения эллипса:

Будем считать, что a>b, и величина, а называется большой полуосью эллипса, ab-малая полуось эллипса.

Параметрическое уравнение позволяет определить точки эллипса с помощью циркуля и линейки. Для этого рисуют две концентрические окружности с центром в натуральных координатах с R=a и r=b.Из натуральных координат выпускаем систему лучей, ставят соответствующую точку, беря абсцессу с большей окружностью, а ординату с малой.

По определению . Точки с координатами (-с;0) (с;0) называются фокусами эллипса, лежат на ОХ. расположений от точек эллипса до его фокусов ,равна постоянной величине 2а.

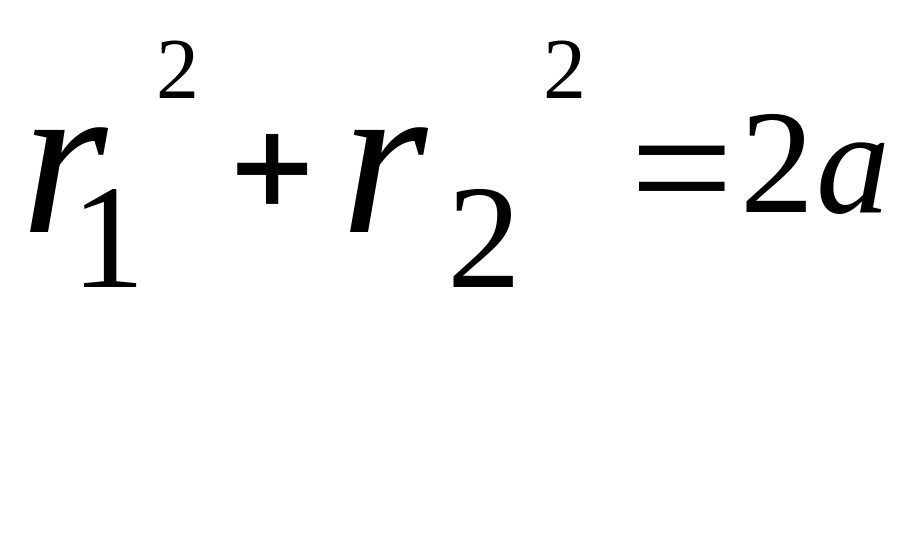(5)

Сумма расстояний от точки, лежащей на эллипсе до его фокусов есть величина постоянная, равная оси эллипса.

Определение: Кривая, точки которой обладает свойством С элементов, связаны такие 2 заметные линии называются директрисами.

Отношение называется эксцентриситетом, для элементов

Директрисами элементов называются прямые, уравнение которых x= Поскольку <1 замечаем, что директрисы проходят не пересекая линию эллипса.

Все точки лежавшие на эллипсе обладают свойством: отношения расположения от точки эллипса до фокуса до фокуса к расстоянию соответствующей директрисы равняется эксцентриситету эллипса. Фокус и директриса, лежащие по одну сторону от начала координат, называются соответствующими друг другу.