Парабола

Определение: параболой называется линия, которая в некоторой декартовой прямоугольной системе координат определяется некоторым уравнением: (3)

Парабола пересекается с осями координат в точке (0;0). Эта точка называется вершиной параболы. Из уравнения (3) вытекает :

1⁰. Ось абсцисс является осью симметрии параболы. Форма параболы известна из школьного курса.

Фокусом параболы называют точку F(P/2; 0). Директрисой параболы называется прямая .

2⁰. Расстояние от произвольной точки параболы до фокуса равно .

3⁰. Точка М лежит на параболе, если она равноудалена от фокуса и биссектрисы ( ).

Принято считать, что .

Аналогично нахождению касательной к эллипсу можно найти уравнение касательной к параболе, которая имеет вид:

.

Поверхность второго порядка

Определение: Геометрическое место точек, координаты которых удовлетворяют уравнению

(4),

называют поверхностью второго порядка.

Первые шесть слагаемых называют квадратичной формой от трёх переменных x,

y, z.

(5)

Квадратичная форма (5) может быть представлена в матричном виде:

(5’)

Следующие три слагаемых уравнения (4) называются линейной формой от трёх переменных:

(6)

В матричном виде уравнение (6) можно представить как

(6’)

Построив новый ортогональный базис из собственных векторов матрицы (5’), приведём квадратичную форму к каноническому виду соответствующей матрицы диагональной формы.

Таким образом поверхность второго порядка можно записать в виде:

(4’)

Величины называются собственными значениями матрицы квадратичной формы. Если собственные значения не равны 0 (≠0), то за счет переноса начала координат уравнение (4’) существенно упрощается:

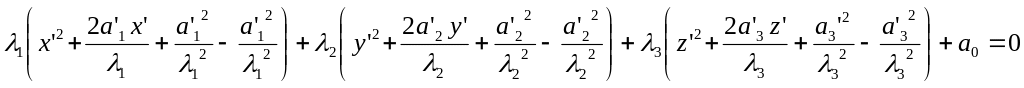
В этом случае уравнение поверхности второго порядка примет вид:

Рассмотрим некоторые канонические формы поверхностей второго порядка.

Поверхности вращения

Определение: Поверхность S называется поверхностью вращения, если ось образована из окружностей, центры которой лежат на прямой, а сами окружности расположены в осях перпендикулярно.

Рассмотрим плоскость P , проходящую через прямую d и линию l, лежащую в плоскости Р. Поверхность вращения можно рассматривать от вращения l вокруг d.

В ыберем на прямой d начало координат О вектор направим по прямой d,

расположим в плоскости Р.

Таким образом на плоскости Р мы вывели декартовую систему координат и линию l можно задать в виде

Возьмем на плоскости вращения точку М (x,y,z) расположенную на окружности радиусом

Точка М лежит на плоскости вращения тогда и только тогда, когда на l существует точка М₁, получаемая из М движением по окружности радиусом r М₁(x,y,z). Точка М₁ лежит в плоскости Р и следовательно y₁=0 z₁=z точки М. координата x₁ по абсолютной величине совпадает с радиусом окружности. М лежит на поверхности вращения, если ее координаты удовлетворяют уравнению

(1) уравнение поверхности вращения может быть также представлено в виде

(1’)