Ранг матрицы

Рассмотрим матрицу A, состоящую из s-строк и n-столбцов.

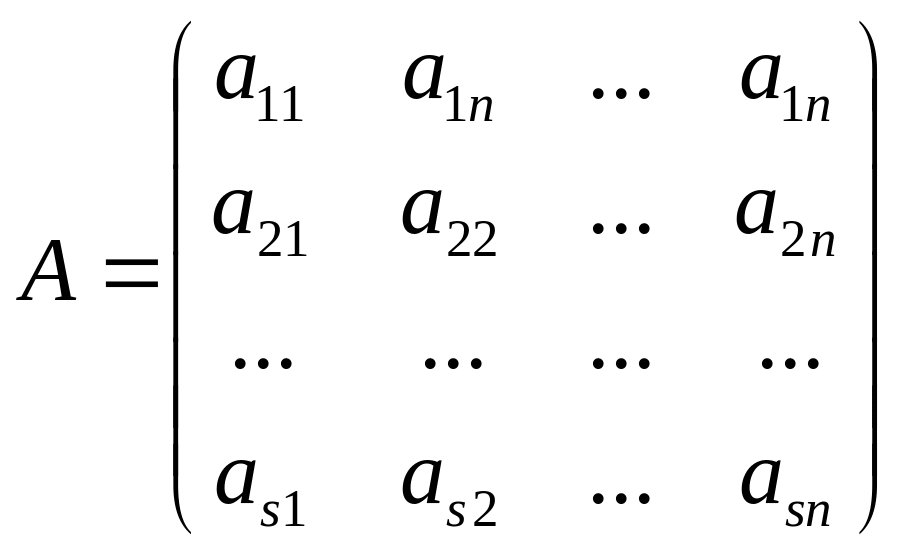
Матрица A можно рассмотреть как совокупность S,n-мерных вектор строк или n,s мерных столбцов.

Определение: Рангом матрицы А называется ранг системы вектор-столбцов матрицы А.

Теорема: Наивысший порядок миноров (≠0) матрицы А равен рангу этой матрицы.

Определение: Вычисление ранга матрицы с помощью сформулированной теоремы, называется методом окаймляющих миноров.

Если найден минор порядка k,а все миноры (k+1) – порядка равны 0,то ранг матрицы равен k.

Ранг матрицы обозначается в виде rang A

Пример: Вычислить ранг матрицы

Следствие 1: Максимальное число линейно независимых строк всякой матрицы равно максимальному число линейно независимых столбцов, т.е. равно рангу матрицы.

Следствие 2: Определитель n-го порядка тогда и только тогда равен нулю, если между его строками (столбцами) существует линейная зависимость. Ранг матрицы может быть также вычислен с помощью элементарных преобразований.

Определение: Две системы векторов называются эквивалентными, если они линейно выражаются друг через друга.

Из определения эквивалентности системы векторов вытекает, что эквивалентные системы векторов обладают одинаковым рангом.

При элементарных преобразованиях строк (столбцов) переходим от системы вектор строк (столбцов) к эквивалентной системе. Таким образом приведя матрицу к диагональному виду с помощью элементарных преобразований найдём ранг матрицы, подсчитав число неравных нулю чисел, стоящих на главной диагонали.

Пример: Вычислим ранг матрицы с помощью элементарных преобразований.

~ ~ ~ =

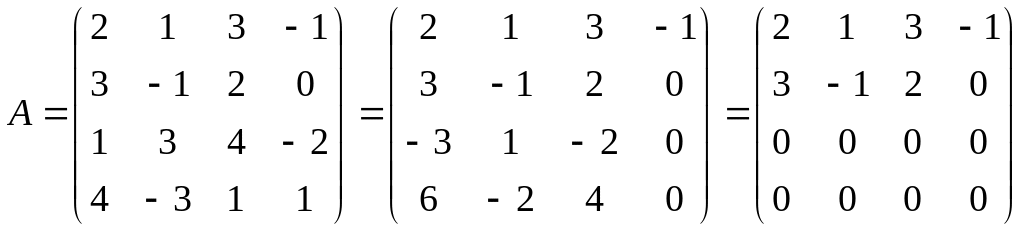
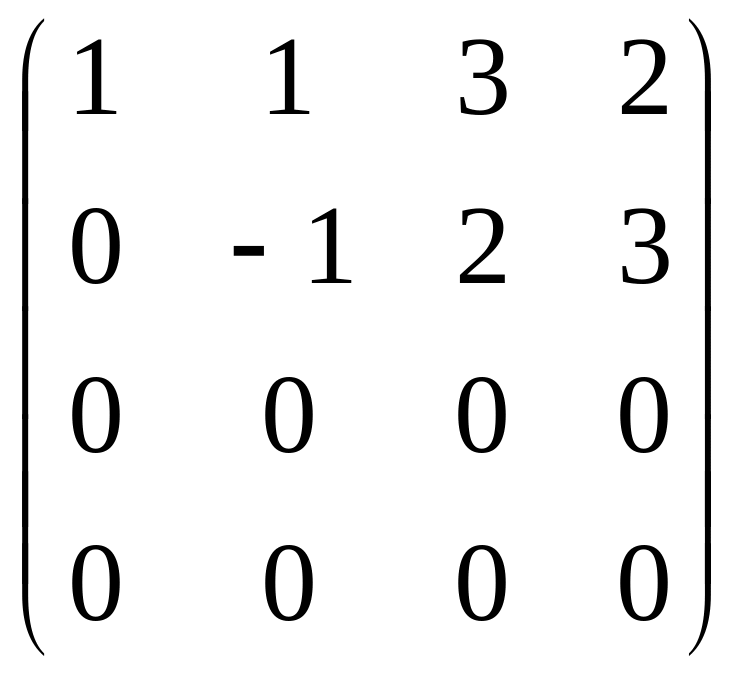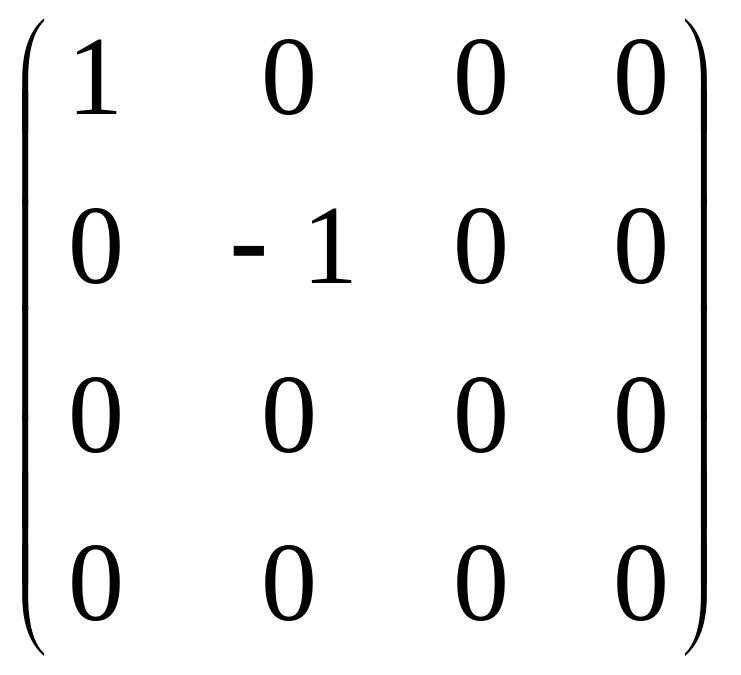Матрица перехода

Рассмотрим линейное пространство V, размерность которой состовляет r.

Пусть и - два базиса пространства V.

Базис a – старый базис, b - новый базис. Разложим каждый из векторов b по базису a.

Записанную систему выражений можно представить в матричном виде

= *

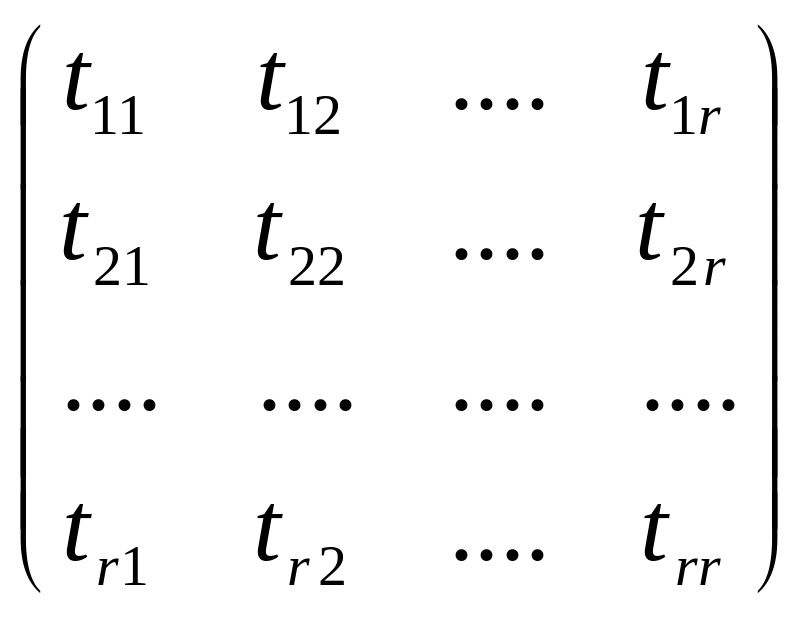
Матрица Т = называется матрицей перехода от старого базиса к новому.

Матрица перехода устанавливает связь между координатами вектора в соответствующих базисах.

Рассмотрим вектор . Пусть в разных базисах координаты в старом базисе.

Этот вектор в новом базисе имеет координаты .

последнее выражение можно представить в матричном виде

* = * .

Используя связь между базисами, устанавливаемую матрицей перехода, записанное выражение представляем:

* = *Т* .

Таким образом устанавливаем связь между координатами вектора в разных базисах.

=Т* . (*)

Выражение (*) определяет старые координаты через новые.

Отметим, что матрица Т – невырожденная, так как вектора системы и системы линейно независимы. Поэтому матрица Т имеет обратную матрицу и из выражения (*) следует, что новые координаты выражаются через старые с помощью обратной матрицы.

=Т^-1* . (**)

Пример: Установить связь между двумя базисами, получаемыми от вращения старого базиса на угол α. Для упрощения выкладок будем рассматривать ортонормированный базис.

Пусть - старый ортонормированный базис.

- новый базис.

Изобразим α на декартовой системе координат.

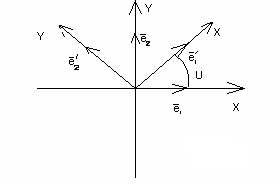
Разложим е₁ по старому базису

U U

U U

Пусть тогда

Пусть в старом базисе найти в новом базисе

Новые координаты вектора a
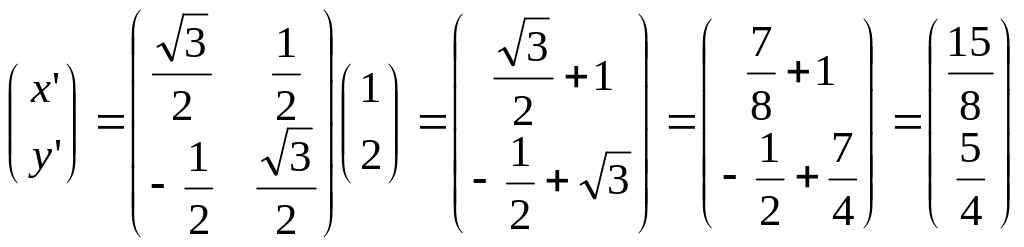