Основные свойства бесконечно малых последовательностей.
Теорема1:
Если
и
- две бесконечно малые последовательности,
то последовательность
также является бесконечно малой
последовательностью.
Доказательство:
Фиксируем некоторое положительное
число
> 0, т.к
является бесконечно малой, то для
заданной величины
найдется номер N,
такой что при всех n
N,
будет выполняться неравенство:
Аналогично для бесконечно
малой последовательности
найдется номер,
такой что при всех n
будет выполняться неравенство
Обозначим в качестве
N
= max
{
}, тогда для всех n
N
будут одновременно выполняться оба
записанные неравенства.
Используя 2 свойство
абсолютной величины,
+
<
+
<
Теорема 2: Разность двух бесконечно малых последовательностей является бесконечно малой последовательностью.
Доказательство теоремы
аналогично доказательству теоремы 1.
Используя 3 свойство абсолютной величины:
-
Следствие Т1, Т2.
Алгебраическая сумма конечного числа бесконечно малых последовательностей дает бесконечно малую последовательность.
Теорема 3:
Произведение
ограниченной последовательности
на бесконечно малую последовательность
дает бесконечно малую последовательность.
Доказательство:
Последовательность
является ограниченной => существует
такое вещественное положительное число
А, что все элементы
Фиксируем положительное
число
> 0. Т.к последовательность
является бесконечно малой, то для
фиксированного числа
найдется номер N
, такой что при всех n
N
будет выполняться неравенство
Таким образом получаем
Откуда следует справедливость теоремы.
Теорема 4:Всякая бесконечно малая последовательность является ограниченной.
Доказательство: Рассмотрим последовательность
Если эта последовательность
бесконечно малая, то для зафиксированного
числа
найдется номер N
, такой что при всех n
N
будет выполняться неравенство
Другими словами все элементы бесконечно малой последовательности начиная с номера N лежат в -окрестности нуля. Вне этой -окрестности находится конечное число элементов.
Обозначим через А = max
Тогда для всех элементов
будет справедливо неравенство
Следствие Т4
Произведение конечного числа всех бесконечно малых последовательностей является бесконечно малой последовательностью.
Теорема5:Если все элементы бесконечно малой последовательности равны одному и тому же числу c, с = 0.
Теорема6:
Если
последовательность
бесконечно большая последовательность,
то начиная с некоторого числа n
определено частное
двух последовательностей
и
,
которое представляет собой бесконечно
малую последовательность.
Если все
элементы бесконечно малой последовательности
отличны от нуля, то частное последовательности
представляет
собой бесконечно большую последовательность.
Сходящиеся последовательности .
Определение1:
Последовательность
называется сходящейся, если существует
такое вещественное число a
, то
является бесконечно малой последовательностью
при этом число a
называется
пределом последовательности
и обозначается
Раскрыв понятие бесконечно малой последовательности дадим второе определение сходящейся последовательности .
Определение2:
последовательность
называется сходящейся к вещественному
числу a
, если для любого числа ε найдется
номер N
, такое что для вех n≥N
будет выполнятся неравенство
(1).
Используя свойство абсолютной величины неравенство (1) можно представить в виде двух неравенств
Неравенство (2) показывает , что начиная с N все элементы последовательности лежат в ε-эпсилонт окрестности точки a.Таким образом можем дать третье определение сходящейся последовательности .
Определение3: Последовательность называется сходящейся, если существует такое число а, что в любой ε- окрестности точки a находятся все элементы последовательности , начиная с некоторого номера.
Согласно первому
определению сходящейся последовательности
замчаем что выражение
является последовательностью
,
которая в свою
очередь является бесконечно малой
последовательностью .
Таким образом элементы
сходящейся последовательностью могут
быть представлены в виде
(3), где a
предел последовательности ,
-
бесконечно малая последовательность .
Свойства сходящейся последовательность сформулированы в виде теорем .
Теорема 1: Сходящейся последовательность имеет только один предел.
Доказательство: предположим противное сходящейся последовательность имеет два предела a и b , тогда элементы последовательности наряду с представлением (3) можно записать в виде
Прировняем наши представления
В правой части последнего неравенства стоит разность бесконечно малой последовательности следовательно бесконечно малая последовательность.
В левой части стоит некоторое постоянное число . Согласно теореме о бесконечно малой последовательности , если бесконечно малая последовательность состоит из одинаковых элементов , то этот элемент равен нулю . Таким образом заключаем , что a-b=0 следовательно что сходящееся последовательность имеет один предел.
Теорема2: Всякая сходящая последовательность ограничена.
Доказательство:
Пусть
сходится к числу а. Фиксируем положительное
число
,по
заданному
находим
N,
таким, что для всех
,будет
выполнятся неравенство:
.Запишем
неравенство в виде:
.Обозначим
через А максимальное из чисел.
А=max
Тогда, все элементы
последовательности
,будут
удовлетворять условию неравенства
,следовательно
последовательность
ограничена.
Теорема 3.Сумма
сходящихся последовательностей
является сходящейся последовательностью,
предел которой равен сумме последовательностей
.
)=
Доказательство:
Т.к.
последовательность
сходятся, то элементы этих последовательностей,
можно представить в виде:
тогда
.Это равенство можно представить в виде:
.В
правой части последнего выражения стоит
бесконечно малая последовательность.
Согласно первому
определению сходящейся последовательности
,сходится
и их предел
.
)=
Теорема 4: Разность двух сходящихся последовательностей представляет собой сходящуюся последовательность, предел которой равен разности пределов последовательностей и .
)=
Теорема 5: Произведение сходящихся последовательностей и представляют собой сходящуюся последовательность, предел которой равен произведению пределов последовательностей и .
)=
.
Пусть последовательности сходятся к числам a и b,тогда элементы этих последовательностей, можно представить в виде: .
Элемент произведения
последовательностей
=
В
правой части бесконечно малая
последовательность. Заключаем, что
является
пределом последовательностей.
Теорема 6: Частное двух сходящихся последовательностей и , предел второй из которых отличен от нуля, определена с некоторого номера. Представляет собой сходящуюся последовательность, предел которой равен частному пределов последовательностей и ,
Покажем, что частное
двух последовательностей определена
с некоторого номера
для
этого нужно доказать, что будет выполняться
неравенство
.
Последовательность
сходится к числу b,
возьмём в качестве
,
число
.
Для этой величины
найдётся номер
,
такой что для всех
,
будет выполняться неравенство
(*).
Представим число b
в виде
Учитывая соотношение (*)
Таким образом получаем,
что
,
для номеров
.
Доказывая отличие от
нуля знаменателя дроби, одновременно
докажем, что последовательность
-ограничена,
так как используя найденные неравенства
можно записать
;
таким образом начиная с номера N*,
можно рассматривать частные
последовательности
Воспользуемся очевидным
тождеством
(сходится к числу а)
Возьмём в записанном
тождестве p=a,
q=b,
получим:
Теорема будет доказана,
если в правой части будет находиться
бесконечно малая последовательность,
используя элементы
,
числитель правой части можно представить
в виде
,
таким образом правую часть можно
представить в виде:
,
получилась бесконечно малая
последовательность в скобках.
Последовательность -является ограниченной, произведение ограниченной и бесконечно малой, даёт бесконечно малую последовательность.
Теорема 7:Если
все элементы сходящейся последовательности
,
по крайней мере, начиная с некоторого
номера, удовлетворяет неравенству
,
то предел х этой последовательности
удовлетворяет этому же неравенству,
.
Доказательство:
пусть все элементы последовательности
начиная с номера
,
удовлетворяет неравенству
,
обозначим предел
последовательности
,
через X,
получим:
.
Предположим противное x<b,
возьмём в качестве
положительную величину
=b-x,
тогда для заданной величины
найдётся номер
,
такой что для всех
,
выполняется неравенство
,
возьмём в качестве
,
тогда для всех
,
должно выполняться неравенство
,
или
,
правая часть последовательности
неравенства, равносильна неравенству,
в системе эти неравенства не могут
выполняться, получим противоречие.
Первая часть доказана, вторая часть доказывается аналогично.
.
Если
последовательности
и
сходятся, и начиная с некоторого номера
выполняется неравенство
,
то и пределы этих последовательностей
удовлетворяют такому же неравенству:
.
Доказательство:
согласно условию теоремы, начиная с
первого номера
Для этого нужно
доказать, что будет выполняться
неравенство
.
Последовательность сходится к числу b, возьмём в качестве , число . Для этой величины найдётся номер , такой что для всех , будет выполняться неравенство (*).
По теореме 7 переходя
к пределу, получим:
Согласно теореме 4
предел разности равен разности пределов:
Это доказывает следствие
.
Если
все элементы сходящейся последовательности
{Xn},
начиная хотя бы с первого номера,
принадлежат отрезку [a,b]
,то и предел также принадлежит [a,b].
Заметим, что требование не строгости неравенства существенны. Заменив неравенства строгим, получим ложное утверждение.
Последовательность,
элементы которой определяются
удовлетворяет
неравенству
.Эта
последовательность является бесконечно
малой и её предел равен 0
.
Теорема 8:Пусть
- две сходящиеся последовательности,
имеющие общий предел а. Пусть, кроме
того, все элементы третей последовательности
,
по крайней мере начиная с некоторого
номера, удовлетворяют неравенству
(4)
Тогда последовательность
(4) справедлива начиная с номера N,тогда
начиная с этого номера будет справедливо
неравенство:
Зафиксируем положительное
значение Е, так
как
-сходящаяся
последовательность, то для выбранного
числа Е найдётся
,
такое, что
будет справедливо
Последовательность
также является сходящейся и для выбранного
значения
,
такое что,
Выберем в качестве N
наибольшее из
3-х чисел
.
Для , будут выполняться неравенства (5), (6), (7),откуда следует, что
Решим задачу о
представлении периодической дроби
6,083131(31) в виде отношения двух чисел
фактически видим последовательность,
затем
находим выражение для n-го
члена
последовательности
Затем вычислим предел
Таким образом, бесконечной периодической дроби поставим в соответствии предел последовательности рациональных чисел. Такой подход в некоторых случаях является боде предпочтительным. С точки зрения этого подхода можно показать, что рациональные числа представляют бесконечные периодические дроби, допускают различные способы записи чисел:
5 или 5,00(0) или
4,99(9)=4+0,9+0,09+…=
Устанавливая взаимодействие соотношения между числовой прямой и вещественным числом, получим последовательность рациональных чисел
Представленный результат вычислим по недостатку с точностью
Исходя из геометрической определённости сходства последовательности, заключаем, что выписанная последовательность является сходящейся, так как для любого положительного числа все элементы последовательности, за исключением конечного числа, находятся в окрестности точки М.
Таким образом число можно определить как предел последовательности рациональных чисел.
Далее приведём предел, что одно и то же число может являться пределом различных последовательностей рациональных чисел.
Если имеется два рациональных числа, то каждому вещественному числу можно сопоставить свою последовательность рациональных чисел. При этом суммой вещественных чисел будет являться предел суммы соответствующих последовательностей. Аналогично можно определить разности произведения и частного.
Пример: Покажем на множестве вещественных чисел, что Ахиллес догонит черепаху.
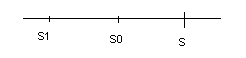
Обозначим через S0, S1, S2 последовательность положений Ахиллеса, тогда S1, S2, … последовательность положений черепахи.
Эти последовательности отличаются первым членом. Отбрасывание конечного числа члена не влияет на сходность.
Ахиллес догонит черепах .если мы покажем, что выписанные последовательности являются сходящимися.
Зададим последовательность точек Ахиллеса рекуррентным соотношением.
, где
Приведя подобные слагаемые, получим
(1)
Уравнение (1) является линейным однородным уравнением относительно
Sn, Sn-1, Sn-2.
Исследуя систему линейных уравнений, показали, что множество решений уравнений является линейным пространством.
В уравнение (1) в правой части стоят две переменные Sn-1, Sn-2, значит пространство последовательностей является двухмерным.
Если мы найдём две линейно независимые последовательности, удовлетворяющие уравнению (1), то любую последовательность, удовлетворяющую уравнению (1) можно представить как линейную комбинацию базисных последовательностей.
Обычно в качестве базисных последовательностей пытаются использовать хорошо известные последовательности. Будем искать базисные последовательности в виде геометрической прогрессии. Подставляя соответствующие элементы геометрической прогрессии, получаем
Приведя подобные слагаемые, сократив на общий множитель
- квадратичное уравнение
относительно q.
α: 1;1;1;…
β: k;k2;k3;…
можем определить последовательность положений А в виде
α
Вβ
А и В определяются математическими условиями
Вычислим предел последовательности
Таким образом, видим, что Ахиллес догонит черепаху в точке S, определяемой соотношением
Подставляя k получим координаты точек встречи, которые совпадают с точками встречи более элементарных соображений
