Следствия из теоремы.

1)Произведение квадратных матриц n – го порядка , содержащих хотя бы одну вырожденную матрицу , является вырожденной матрицей.

2)Произведение невырожденных матриц , является невырожденной матрицей.

Роль единицы при умножении матриц играет единичная матрица . Единичную матрицу обозначают E и она состоит из единиц, расположенных выражений.

вычислим определитель из левой и правой части записанного , таким образом замечаем, если А не вырожденная, то присоединенная матрица А*, также является не вырожденной, причем: , аналогичный результат получается при рассмотрении произведения , заметим, что если матрица С= и если элементы одной из перемножаемых матриц разделит на некоторое число, то все элементы матрицы С разделятся на это число. С учётом сделанного замечания

(5)

Выражение (5) позволяет вычислить обратную матрицу.

Пример 1: вычислить обратную матрицу матрицы А.

;

матрица не вырожденная, следовательно, она обладает обратной матрицей. Вычислим алгебраически дополнительные элементы матрицы А.

, наряду с формулой (5), обратная матрица может быть

вычислена с помощью элементарных преобразований, для этого составляют дополнительную матрицу, приписывая к матрица А единичную матрицу вправо, создают единичную матрицу в левой части, а в правой части появится обратная матрица.

П ример 2: с помощью элементарных преобразований, найти матрицу, обратную матрице А.

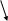
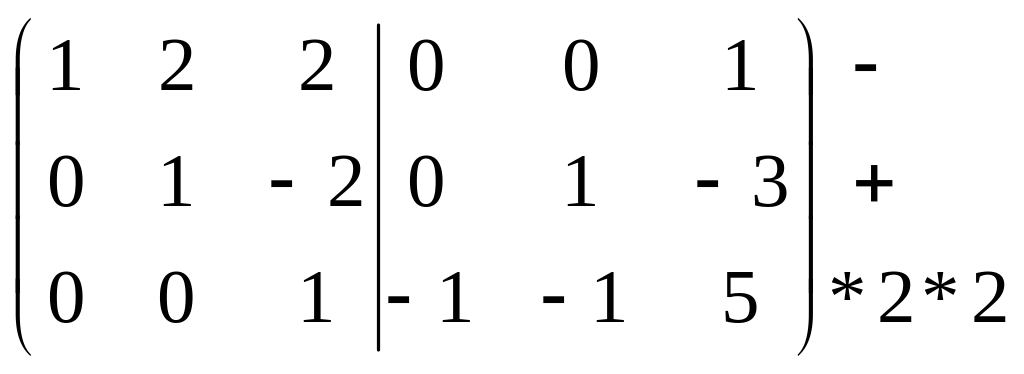
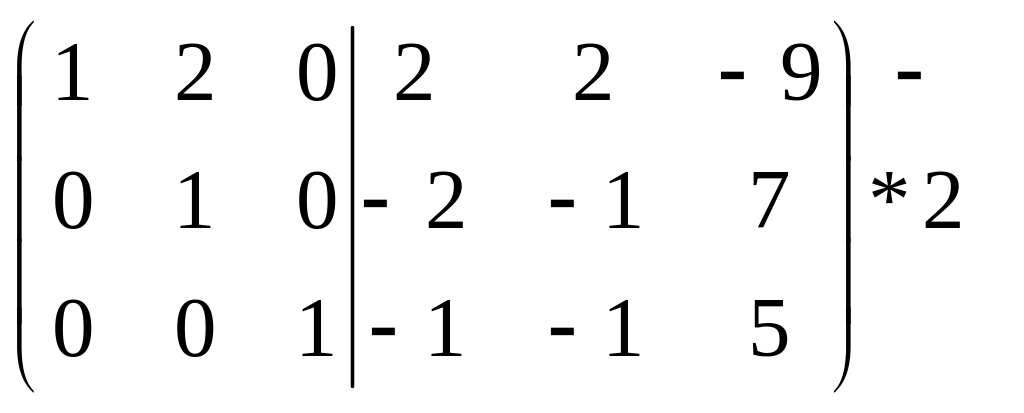
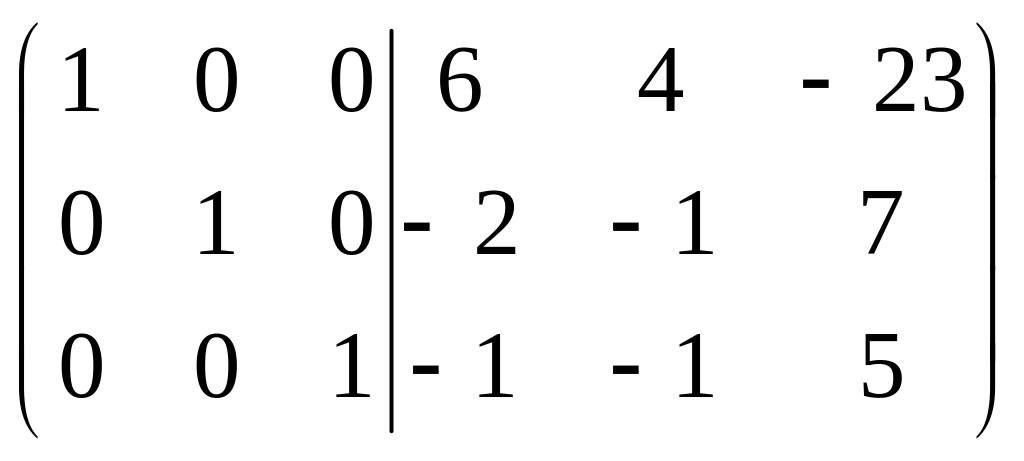
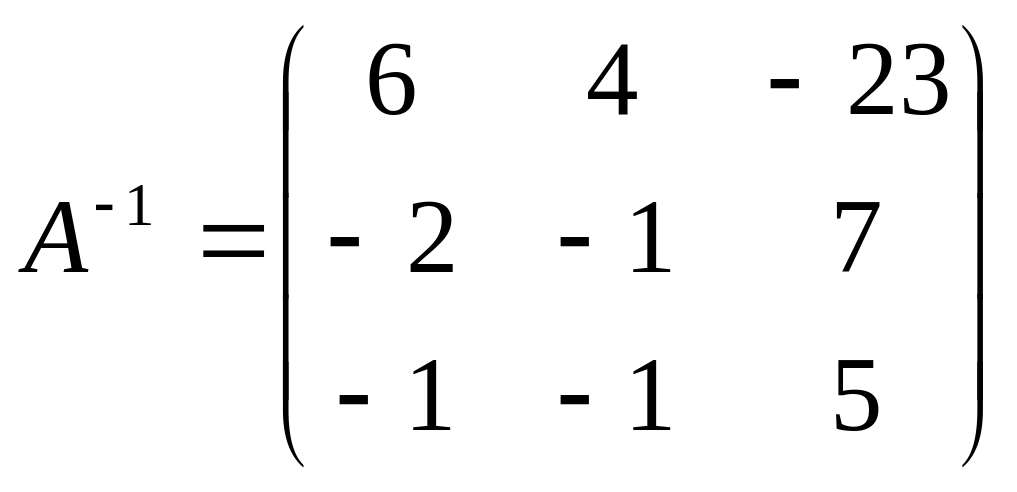
Решение матричных уравнений

Пусть даны две матрицы A и B, причем A-невырожденная и 2 неизвестная матрицы X, Y. С помощью обратной матрицы можно решать уравнения вида:

A*X=B (1)

Y*A=B (2)

Для решения уравнения (1) умножаем обе части на матрицу обратную к А слева

в силу ассоциативности матриц левую часть уравнения представим в виде

произведение, стоящее в скобках

умножение на ед. матрицу не изменяет матрицу Х. Чтобы Y*A=B необходимо умножить на обратную матрицу справа

в силу ассоциативности

- решение уравнения (2)

Пример: решить матричным способом систему линейных уравнений:

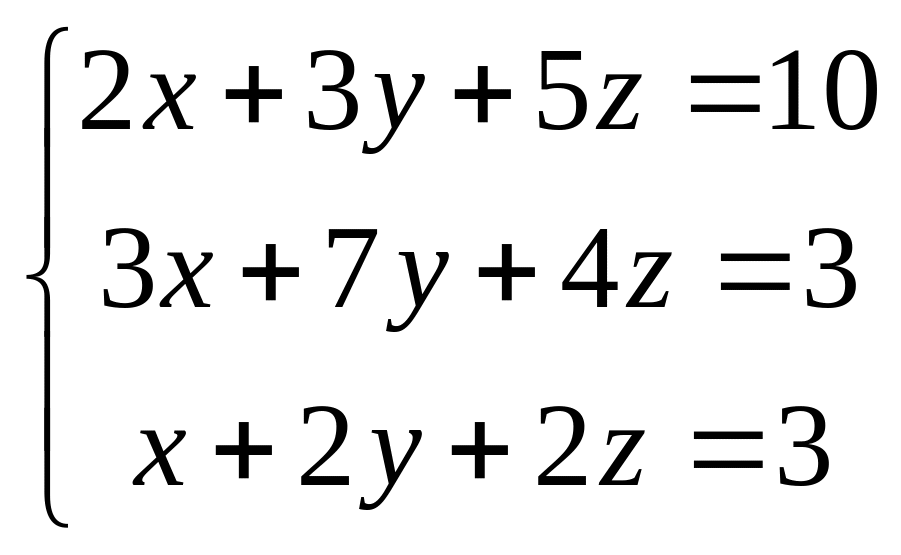
Представим систему уравнений в матричном виде

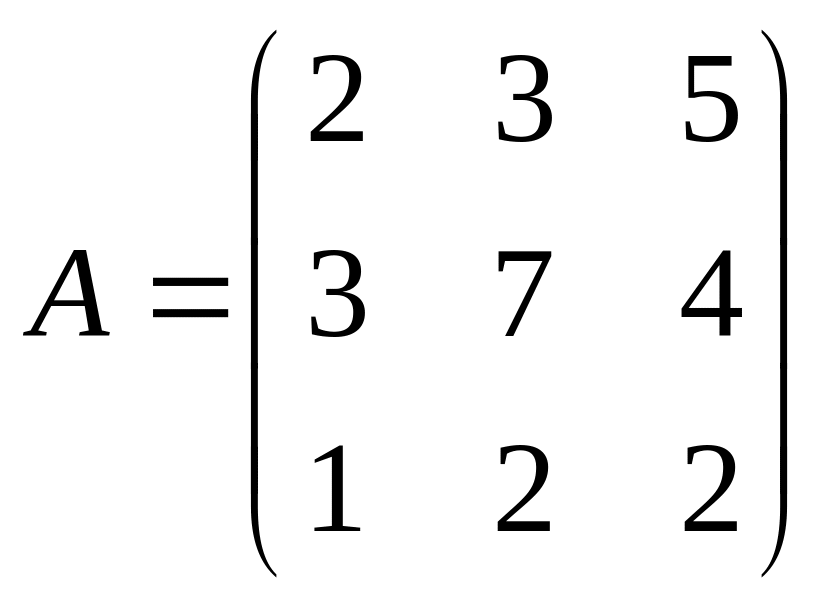
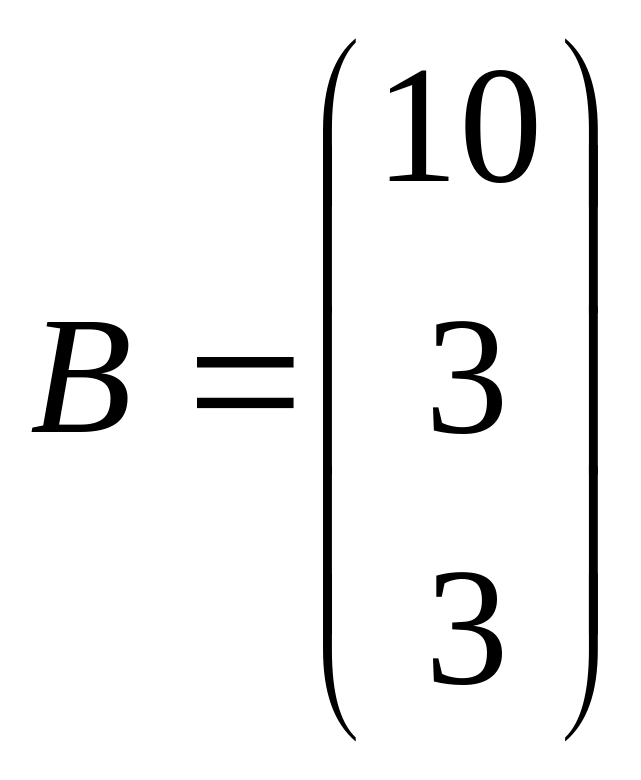
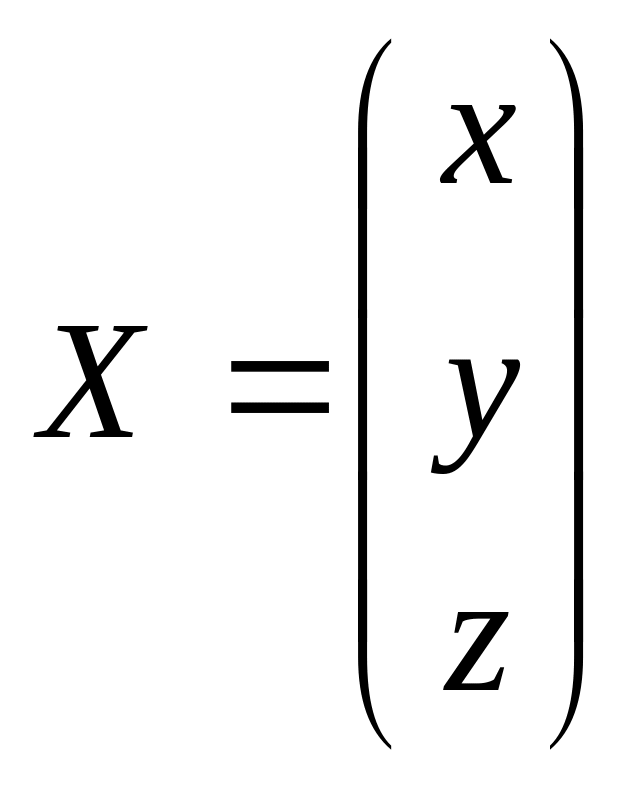
При этом систему уравнений можно представить в виде

A*X=B

Решением которой -> X=A^-1B

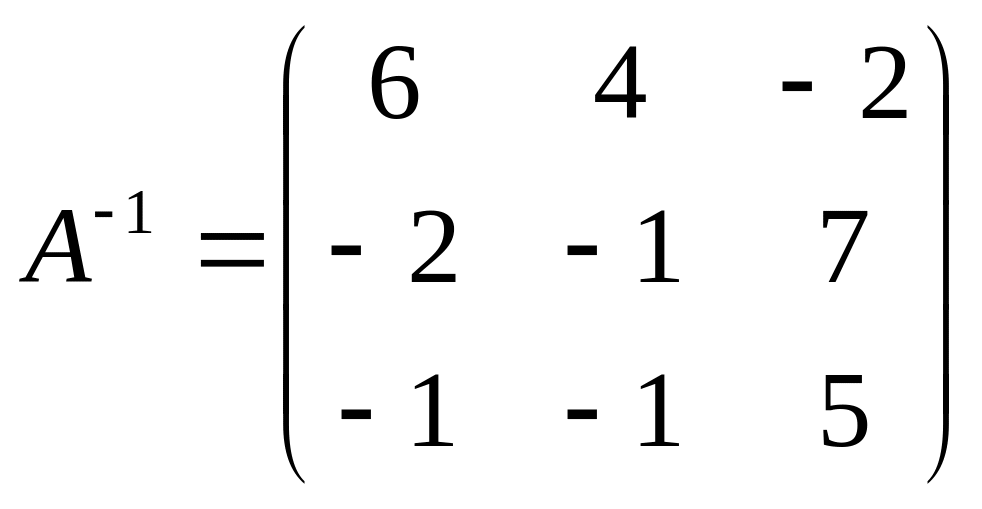
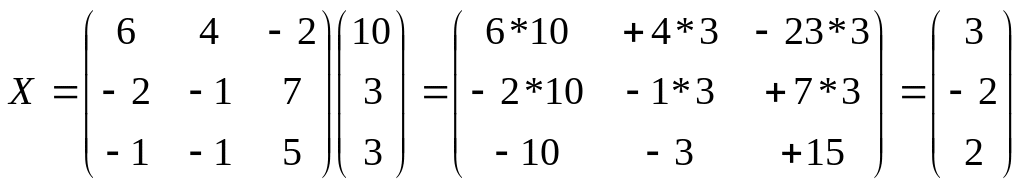x=3, y=-2, z=2

Комплексные числа

Рассмотрим множество квадратных матриц вида:

,где x, y – некоторые вещественные числа. Покажем, что множество таких матриц замкнуто относительно алгебраических операций. Рассмотрим двух матриц.

Рассмотрим произведение матриц:

Множество матриц замкнуто относительно умножения.

Множество матриц замкнуто относительно сложения и вычитания.

3) найдём обратную матрицу.

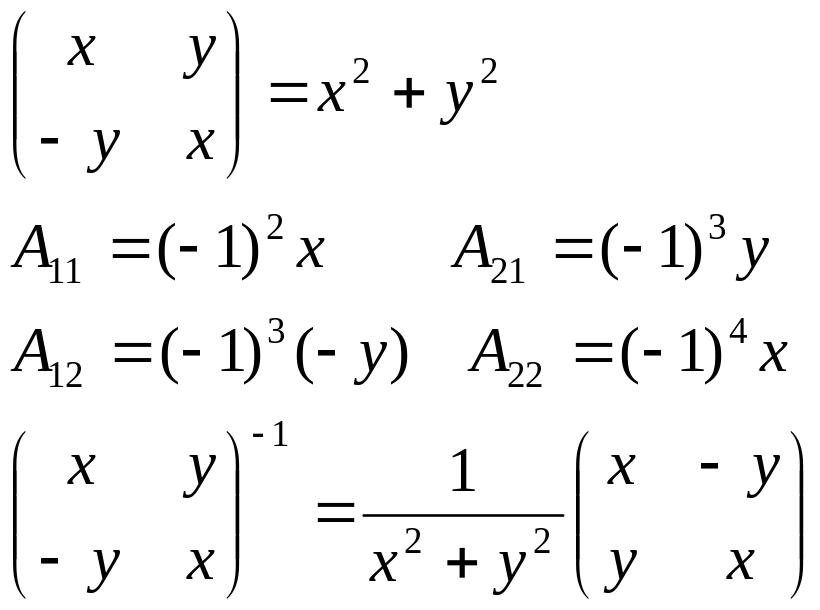
Матрица такого же строения

Из курса школы известно, что уравнение не имеет решения.

Докажем, что на множестве рассматриваемой матрицы, уравнения такого типа разрешимо.

Найдём решение уравнения:

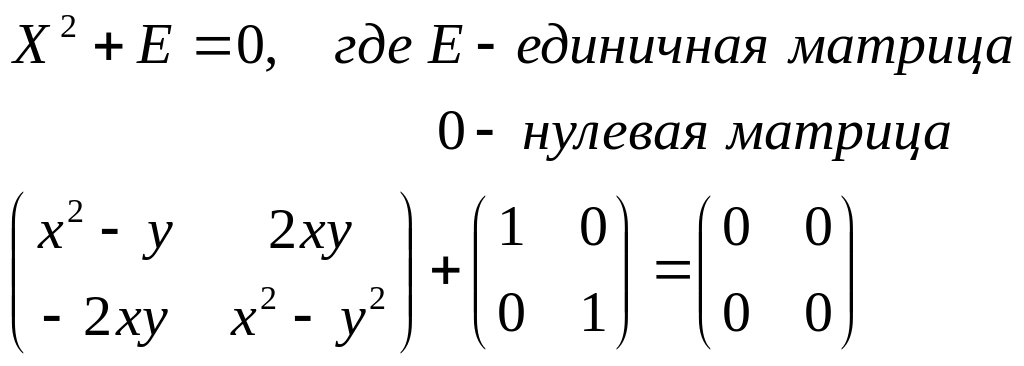
Отметим, что единичная и нулевая матрицы представимы в виде (3)

Откуда приходим к системе уравнений:

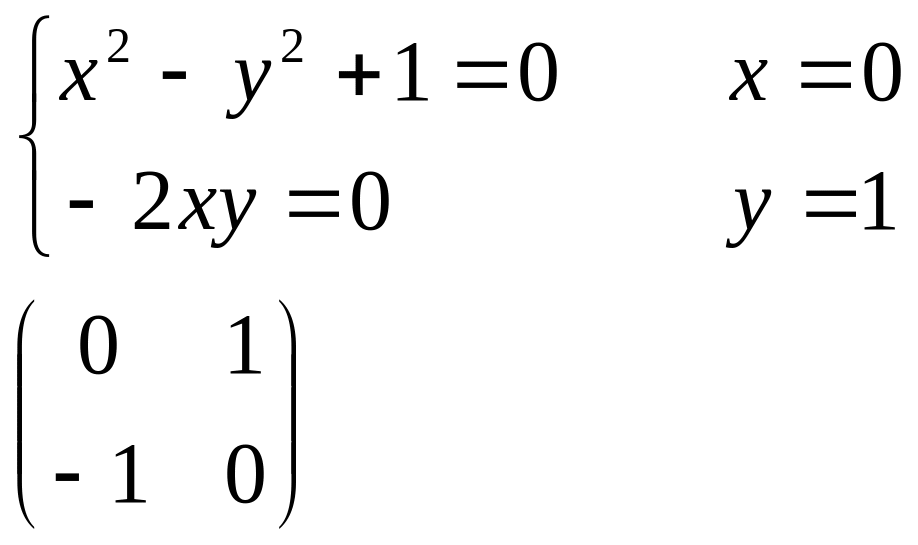
Каждая матрица вида (3) определяет упорядоченным набором двух действительных чисел x, y.

Определение: Упорядоченную пару действительных чисел x, y называют комплексным числом (x,y)

Матрицу вида (3) можно представить в виде

Со времен Эйлера и Гаусса матрицу принято обозначать символом I, в связи с чем комплексное число принято записывать x+Iy=x+iy.Каждая упорядоченная пара действительных чисел изображается точкой на плоскости.

Ось абсцисс – действительная ось и обозначается R_e (Real). Ось ординат – I_m (Image). Комплексные числа обозначают z = x + i*y, тогда

x = R_eZ ;

y = I_mZ;

Если множество действительных чисел изображается точками на числовой прямой, то множество комплексных чисел изображается точками на числовой плоскости.

Комплексное число можно трактовать как радиус-вектор, выходящий из начала координат.

Расстояние . Это расстояние называется |Z| (модуль комплексного числа Z). Угол между действительной осью и радиус-вектором, отсчитанный против часовой стрелки, называется аргументом комплексного числа.

Иногда аргумент пишут с большой буквы, подразумевая величину угла с учётом периода.

если точка в первой четверти

Наряду с арифметической записью z = x + i*y с помощью понятия модуля и аргумента комплексное число представляют в тригонометрическом виде.

Некоторые алгебраические операции проще выполняются с помощью тригонометрических чисел. Комплексное число , называется комплексным числом, сопряжённым числу z.

симметрична точке z относительно действительной оси.