Линейные преобразования

Пусть задано линейное пространство V, - производный элемент пространства V,( ),отображение ,ставящее в соответствие элементу , некоторый элемент называется преобразованием. Преобразования принято обозначать

При этом элемент называют образом элемента , а элемент называют праобразом элемента .

Определение: Преобразование линейного пространства V,называют линейным ,если выполняются два требования:

Образ суммы равен сумме образов

,где некоторое число из второго требования вытекает, что при линейном преобразовании нулевой элемент остаётся неподвижным

Образ противоположного вектора равен

Разложим произведение элемент по базису пространства V,где вектора образующего базис пространства V.

, используя первое требование линейности образ вектора можно представить в виде.

Используя операцию умножения матриц, образ можно представить в виде.

Соотношение (1) показывает, что линейные преобразования полностью определяются заданием образов базисных векторов. Образы базисных векторов лежат в рассматриваемом пространстве V и поэтому могут быть разложены по базису этого пространства.

(2)

Представим соотношение (2) в матричном виде

(3)

Матрица, стоящая в соотношении (3), называется матрицей линейного преобразования.

Разложив вектор по базису , получим, что можно представить в виде:

(4) Подставив соотношения (3) и (4) в (1), найдём

Откуда следует .что координаты образа определяются координатами праобраза соотношением (5)

(5)

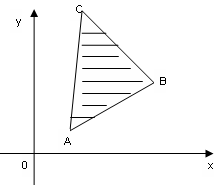
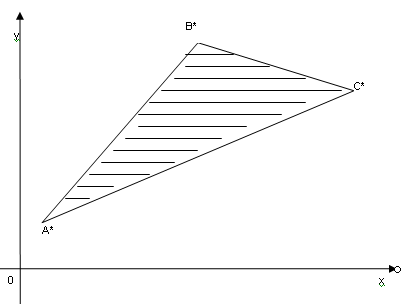
Пример: Найти образ треугольника ABC, определяемый линейным преобразованием, заданным соответствующей матрицей.

Пусть точка А имеет координаты (2,1), точка В – (5,3), точка С – (3, 6).

-заданная матрица преобразования

Изменение матрицы линейного преобразованиями при переходе к новому базису

Пусть - старый базис V

- новый базис V

Связь между старым и новым базисами определяется с помощью матрицы перехода Т

Пусть - произвольный элемент пространства V его координаты в старом базисе

в новом

Пусть образ вектора , координаты образа в старом базисе

в новом

Пусть А матрица линейного преобразования в старом базисе, тогда координаты образа с координатами праобраза определяются соотношением

(6)

Учитывая связь между координатами вектора в старом и новом базисах, устанавливаемую матрицей перехода Т

Соотношение (6) можно переписать в виде

(7)

Разрешая матричное уравнение (7) относительно столбца y’ , получим

(8)

Соотношение (8) показывает, что матрица преобразования в новом базисе А’ определяется выражением

(9)

Определение: Две матрицы В и С называются подобными, если существует такая невырожденная матрица Q, что имеет место соотношение

Формула (9) показывает, что матрицы, определяющие одно и то же линейное преобразование в разных базисах подобны между собой.

Собственные вектора и собственные значения

Определение: Отличный от 0 вектор называется собственным вектором линейного преобразования, если выполняются соотношения (10) , число называют в этом случае собственным значением.

Укажем алгоритм нахождения собственных векторов и собственных значений.

Пусть линейное преобразование задано в некотором базисе матрицей А. Вектор определяется в заданном базисе столбцом своих координат, тогда соотношение (10) можно переписать в виде:

Перенеся всё в левую часть, получим:

(11)

Уравнение (11) относительно неизвестных ( , ,…, ) является системой линейных однородных уравнений.

Система (11) будет иметь отличные от нуля решения только в том случае, когда rang < n; другими словами, когда определитель (12)

Уравнение (12) называют характеристическим многочленом относительно переменной

Найдя корни характеристического многочлена (12), найдем собственные значения линейного преобразования. Подставив найденные значения в (11), получим неопределенную систему линейных однородных уравнений.

Вектора, образующие фундаментальную систему решений системы (11) будут являться собственными векторами.

Пример: Найти собственные значения и собственные вектора линейного преобразования. Заданного матрицей А.

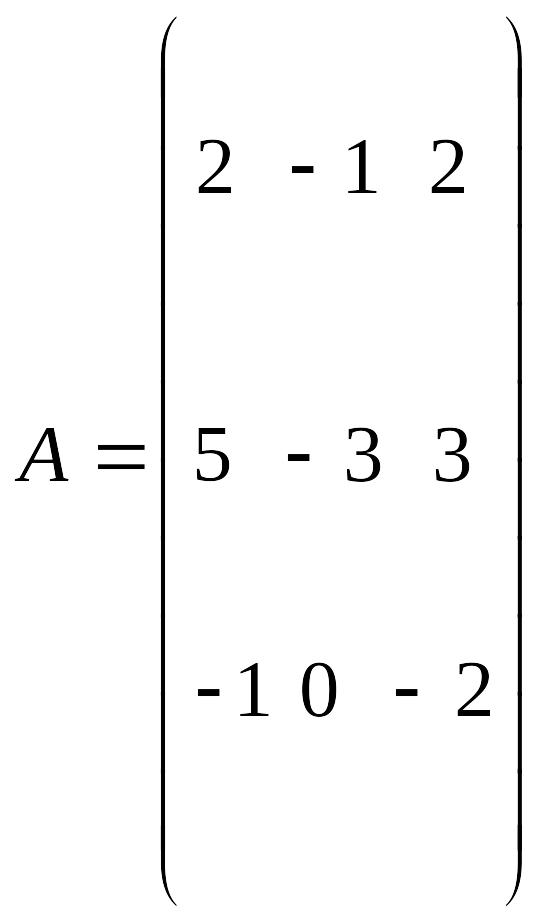
Составим характеристический многочлен

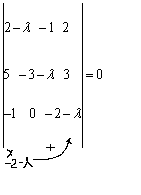
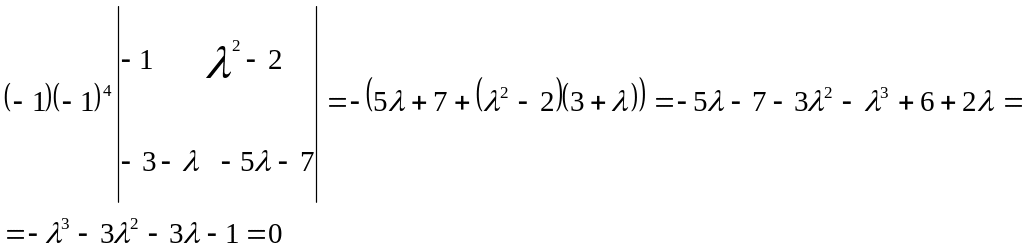
Найдем собственные вектора

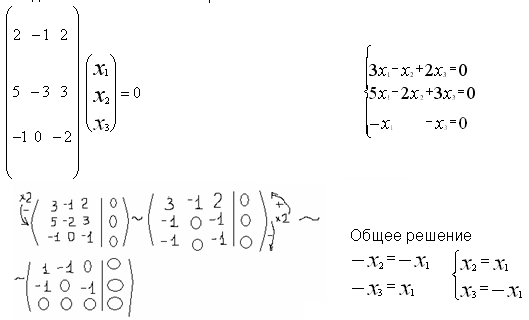
	1	1	-1

Найдем образ вектора

Покажем , что собственные значение подобных матриц совпадают .

Пусть матрицы A и B подобны

Рассмотрим характеристические многочлены A и B.

Характеристический многочлен матрицы A и B.

Используя представления матрицы B через A

Учитывая свойства обратной матрицы

Тогда

Воспользовавшись теоремой об определители произведения матриц

Следовательно, что характеристические многочлены подобных матриц совпадают.

Отметим, что матрица линейных преобразований приводятся к диагональному виду тогда и только тогда , когда существует базис ,составленный из собственных векторов линейного преобразования.

Пусть - собственные вектора линейного преобразования, тогда , , .

Тогда