Разложение определителя по строке (столбцу).

Пусть некоторый элемент определителя. Алгебраическое дополнение элемента .

Произведение состоит из (n-1)!. Выпишем все элементы i-той строки определителя n-го порядка. .Для каждого элемента строки образуем произведение.

Согласно ранее приведённой теореме в каждом из записанных произведениях содержится (n-1)! слагаемых, которые также являются слагаемыми исходного определителя n-го порядка. Видим, что среди выписанных произведений не может быть одинаковых слагаемых. Подсчитаем число слагаемых выписанном произведении (n-1)!*n=n!

Таким образом, видим, что в выписанном произведении содержаться все слагаемые определителя n-го порядка можем записать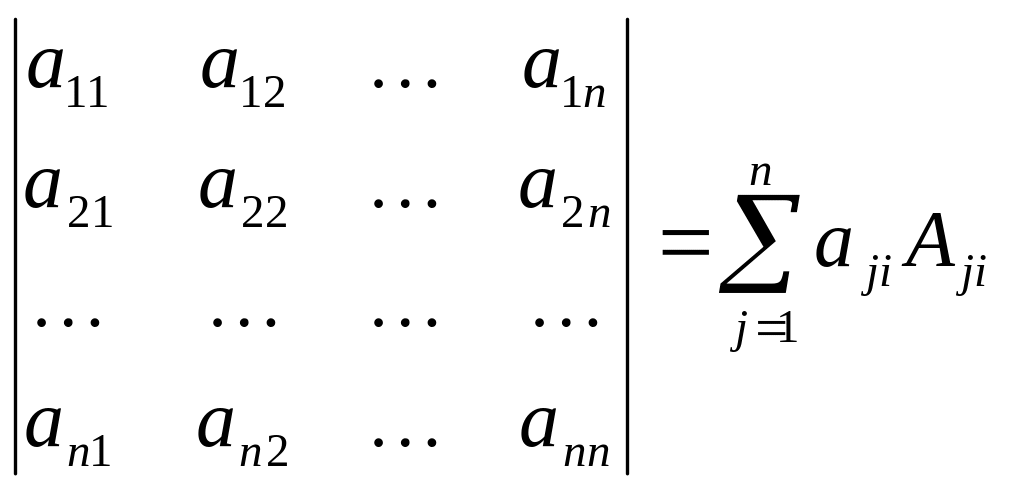

Согласно первому свойству определителя разложение справедливо не только для строк, но и для столбцов. Сформулируем полученный результат в виде теоремы.

Теорема: Определитель n-го порядка равен сумме произведений элементов произвольной строки (столбца) на их алгебраическое дополнения.

Пример: Вычислить определитель.

Разложим этот определитель по второй строке.

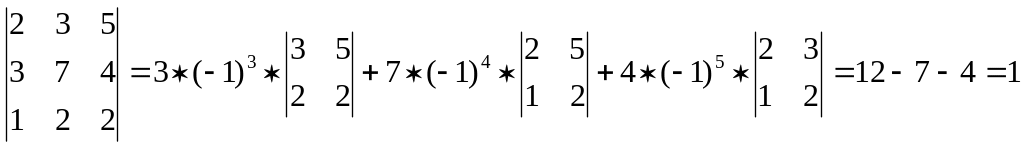
Разложим этот определитель по третьему столбцу.

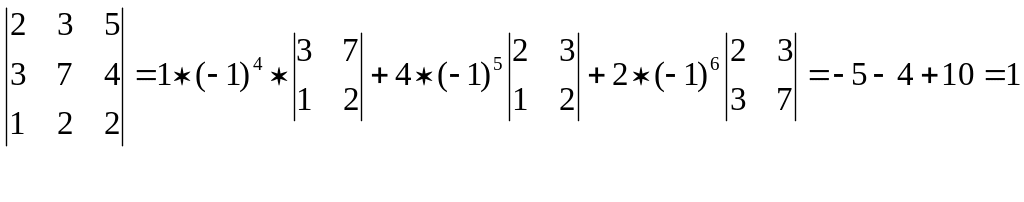
На практике для вычислении определителя предварительно его упрощают, используя свойство определителя.

Согласно девятому свойству определитель не изменится, если к элементам столбца добавить элемент другого столбца, умноженный на k.

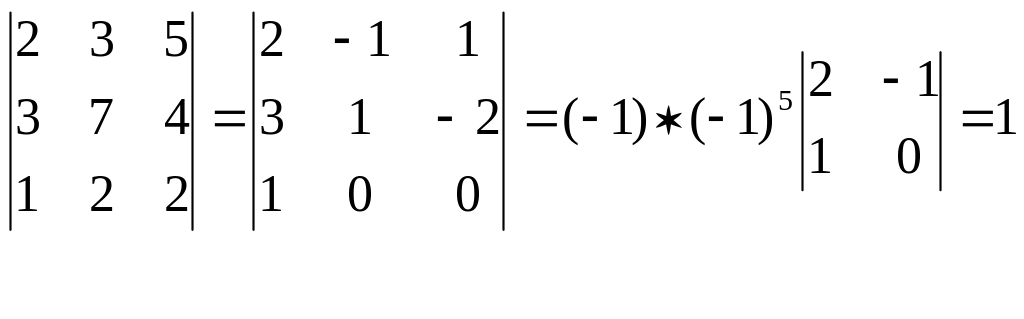
Правило Крамера

Лемма: Сумма произведений всех элементов некоторого столбца определителя на алгебраические дополнения соответственных элементов другого столбца равна 0.

Доказательство: Рассмотрим определитель n-го порядка

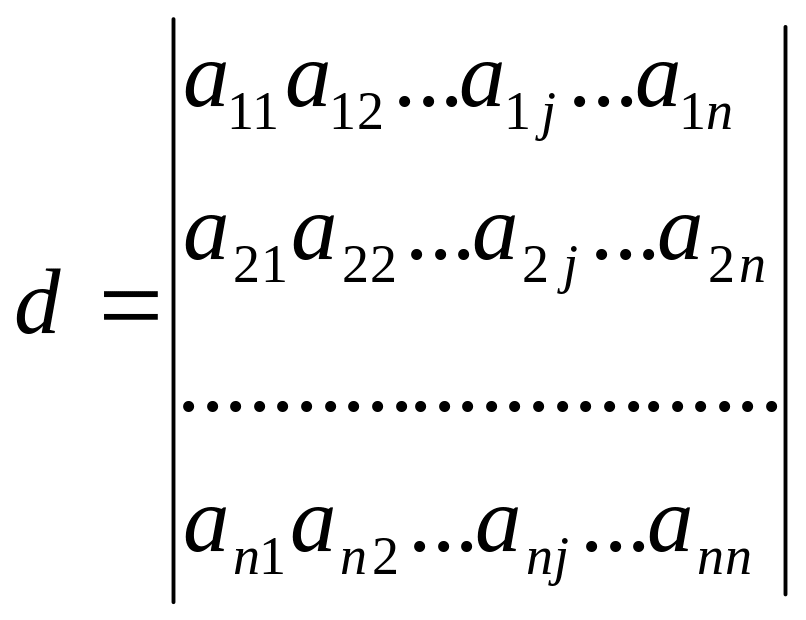
Разложим определитель по j-му столбцу.

Заменим в определителе d по j-ому столбцу столбцом , получим

Так же разложим определитель по j-ому столбцу.

Заменив в определителе d_j столбец b любым из оставшихся столбцов, получим определитель

Заметим, что определитель будет содержать два ( ) одинаковых столбца , поскольку k-ый столбец мы поставили вместо j-ого столбца.

Согласно свойствам определителя, если в определителе содержится два одинаковых столбца, то он равен 0.

Рассмотрим определённую систему линейных уравнений n-ого порядка.

(2)

Пусть набор чисел является решением системы (2). Подставляя величины вместо неизвестных, получим систему тождеств (3).

(3)

Возьмём число j из множества первых n натуральных чисел. Умножим первое тождество на , второе – на , … , n-ое – на , где алгебраические дополнения вычисляются с помощью определителя n-ого порядка, составленного из коэффициентов системы (2).

Сложив полученные тождества, придём к выражению

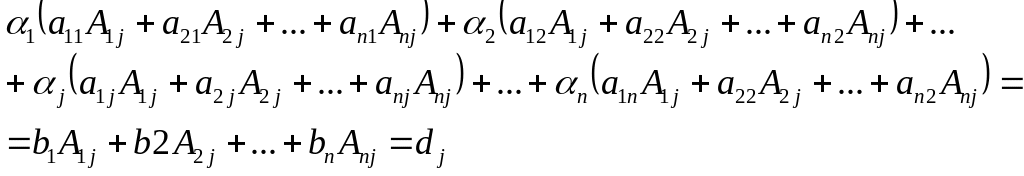
Коэффициент при является разложением определителя коэффициентов по j-ому столбцу и он равен . Остальные коэффициенты при в левых частях равны сумме произведений элементов некоторого столбца на алгебраические дополнения соответствующих элементов другого столбца.

Согласно лемме, все эти коэффициенты равны 0. Выражения, стоящие в правой части при доказательстве леммы обозначают . Таким образом получили выражение (4)

Покажем что система чисел (4) удовлетворяет системе (2)

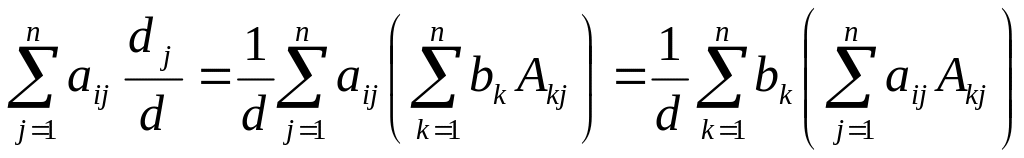
Подставим уравнение системы (2) и подставим в него значение (4)

Выражение, стоящее в круглых скобках =0, если (согласно лемме) если то выражение в скобках равно определителю d. Система (4) действительно является решением системы (2). Получаем решение системы называемое правилом Крамера.

Обобщение теоремы о разложении определителя по строке (столбцу). Теорема Лапласа.

Пусть в определителе d выбрано k строк (столбцов), где , тогда произведений всех миноров, располагаемых в k-строках (столбцах) но их алгебраические дополнения равны определителю d.

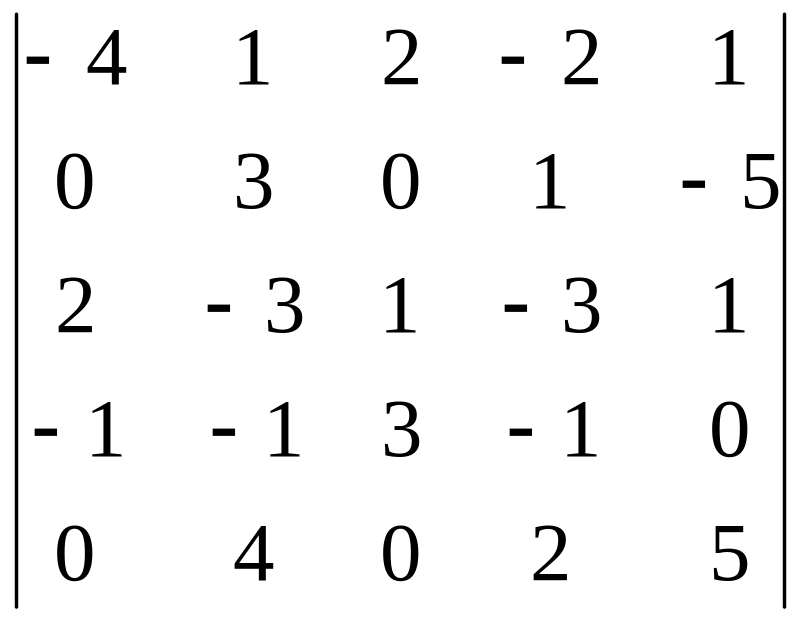= (Разложим этот определитель по 1 и 3 столбцам.)

=

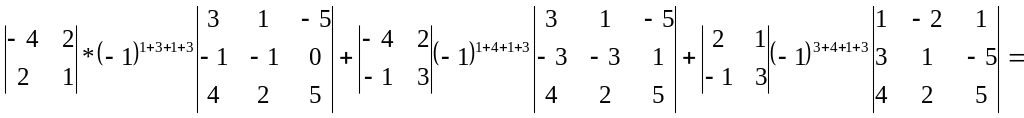
Основные операции над матрицами

а) Две матрицы А и В называются равными, если они имеют одинаковые размеры и если их элементы, стоящие на одинаковых местах, совпадают.

b) Суммой двух матриц А и В одних и тех же размеров называется матрица С тех же размеров, элементы которой определяются размером:

(1)

Из формулы (1) вытекает, что сложение матриц обладает коммутативностью и ассоциативностью

с) Произведением матрицы А на q называется матрица С элементы которой определяются выражением

(2)

Из формулы (2) вытекает что умножение матрицы на число обладает: Ассоциативностью относительно числовых множителей

Дистрибутивностью относительно числовых множителей

И дистрибутивностью относительно матриц

d) Умножение матриц.

Пусть имеется матрица А размером m на n, и матрица В размером n на p, тогда произведением матриц А на В называется матрица С размера m на p, элементы которой определяются выражением

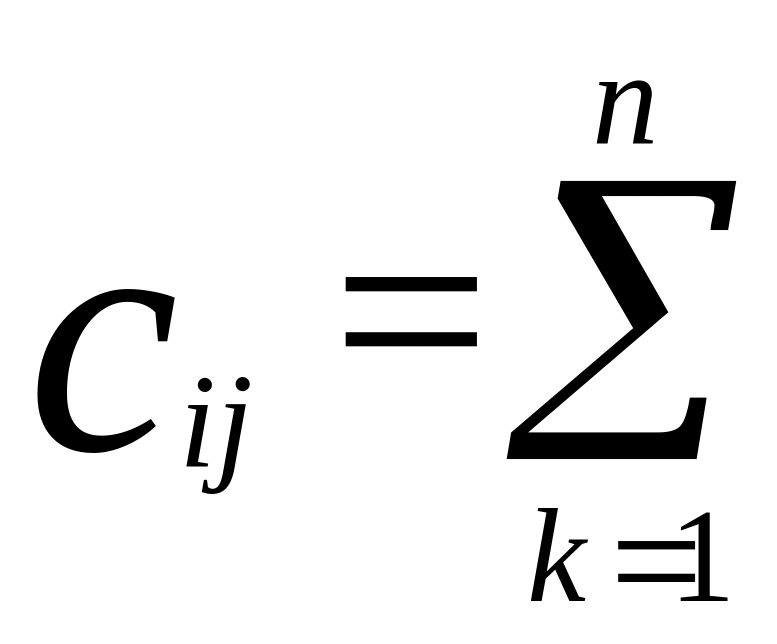
(3)

Из формулы (3) заключаем, что умножение матриц определено, когда число столбцов матрицы А совпадает с числом строк матрицы В.

Чтобы получить элемент нужно элементы i-строки матрицы А перемножить с соответствующими элементами j-столбца матрицы В.

Формулу (3) называют правилом строки на столбец.

Пример:

А = , В =

Матрица А имеет размеры 2 на 3, В – 3 на 2.

Видим что заданные матрицы можно перемножить.

АВ = = =

Перемножим эти матрицы в обратном порядке.

ВА = = =

Приведенный пример показывает, что умножение матриц не обладает коммутативностью, причем умножение матрицы в различном порядке поможет приводить к матрицам различных размеров. Для того чтобы при умножении матриц в различном порядке сохранились размеры, перемножаемые матрицы должны быть квадратными, одного и того же размера.

Из формулы (3) вытекает, что умножение матриц обладает ассоциативностью

А (ВС) = (АВ) С

и левой и правой дистрибутивностью

А (В+С) = АВ + АС

(В+С) А = ВА + СА

Теорема: Определитель произведения нескольких квадратных матриц равен произведению определителей.

Доказательство: В силу ассоциативности умножения матрицы достаточно рассмотреть случай произведения двух матриц, т.е. достаточно доказать, что det (AB) = det A * det B.

Выпишем вспомогательный определитель порядка 2n

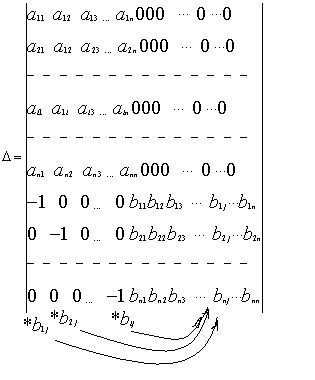
Видим, что в верхнем левом углу определителя стоят элементы матрицы А.

Стоят элементы матрицы А в правом нижнем углу определителя , стоят элементы матрицы В . Правый верхний угол определителя состоит из нулевых элементов . Левый нижний угол содержит 1 по главной диагонали и нули на остальных местах . Вычислим определитель по 1 n- строкам воспользовавшись теоремой Лапласа.

=detA detB=detA*debB

Преобразуем определитель , не меняя его значения .Создадим нули в правом нижнем углу определителя . При этом нули в правом верхнем углу исчезнут .

Выпишем элемент , который при таких преобразованиях окажется на пересечении i-той строки (n+j) строкой .

Сравнивая получаем выражение с формулой (3) , замечаем что получаем значение ,являющегося произведением матрицы А на В . То образуется , выполнив преобразования определителя .

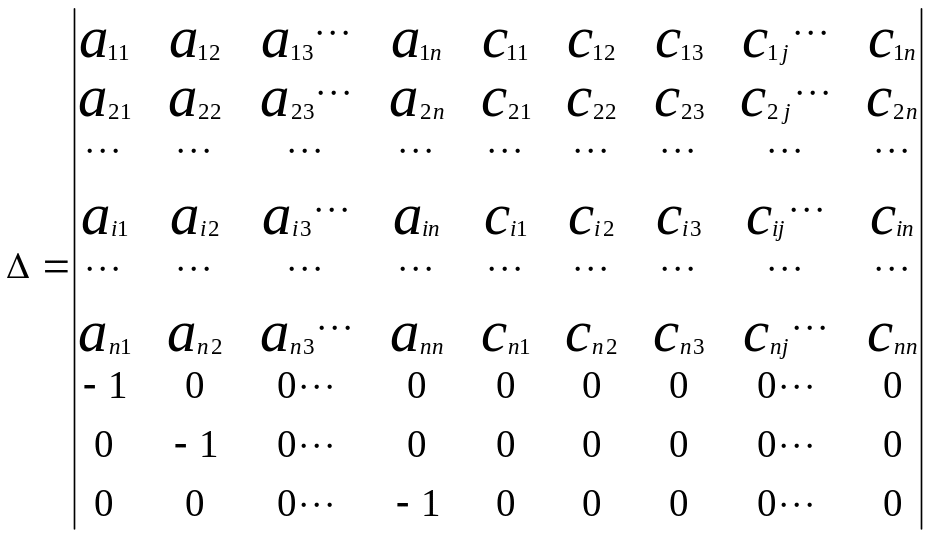
Вычислим определитель разложив по последующим n столбцам.

= detC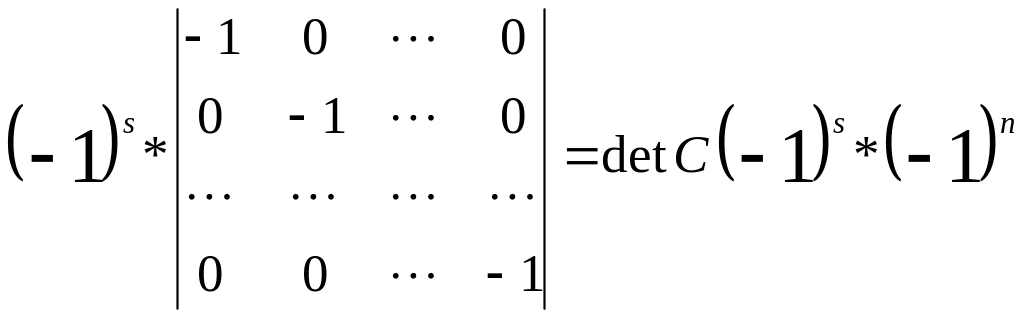

Подсчитаем число 3. S = 1+2+3+4+...+n+(n+1)+(n+2)+...+2n=(1+2n/2)*2n=n+2

Воспользовавшись формулой для сумм арифметической прогрессии и определитель будет равен

Таким образом получим , что определитель матрицы C (detC)

det(C)=det(AB)=det(A)det(B)

Определение: квадратная матрица называется вырожденной (особенной) , если ее определитель (det) =0.