Двуполостный гиперболоид

Будем вращать гиперболу относительно действительной оси:

Т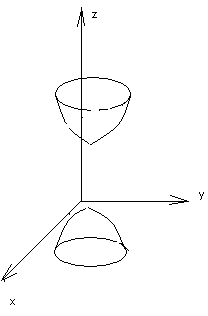 огда уравнение поверхности вращения будет иметь вид:

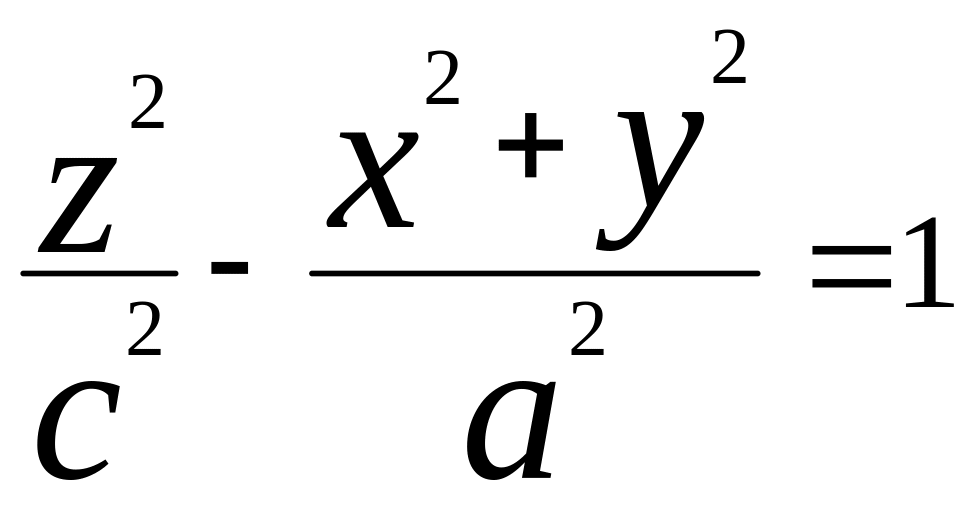
Поверхность движения гиперболы вращения распадается на две непересекающиеся части. Сжав поверхность вращения гиперболы к плоскости y=0,получим поверхность, уравнение которой имеет вид: ,и называется двуполостной гиперболой.

Так же как и для однополосной гиперболы, для двуполостной гиперболы вводится понятие ассиметричная гипербола.

Эллиптический параболоид

Рассмотрим поверхность, получаемую при вращении параболы вокруг её оси симметрии. Уравнение параболы возьмём в виде: , в этом случае ось симметрии совпадает с осью z, в этом случае поверхность вращения будет иметь вид:

Сделав точки параболоида вращения в плоскость Y=0, получим поверхность уравнение которой имеет вид: . Соответственно поверхность называется эллиптическим параболоидом. Сечения этой поверхности x=const,(y=const)-будут являться параболами сечения плоскостями. z=const будут являться эллипсами.

Гиперболический параболоид

Определение: Поверхность, которая имеет в некоторой декартовой системе координат уравнение , называется гиперболическим параболоидом.

Сечение гиперболического параболоида x=const,(y=const), будут определять параболы сечения гиперболического параболоида, сечение z=const будут определять гиперболы. Поверхность гиперболического параболоида можно определить, заставив одну параболу двигаться по другой параболе, оси которых параллельны, а ветви направлены в противоположенные стороны.

Как и у однополостного, у гиперболического параболоида существуют две системы. Разложив левую часть системы (*) на множители, получим: .

И можно записать две системы в виде:

и

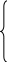
Математический анализ

Вещественные (действительные) числа

Начнём с изучения множества натуральных чисел N. Натуральными числами называются числа, которые используются при счёте (1, 2, 3, 4,.....).

Расположение натуральных чисел в порядке их возрастания называют натуральным рядом.

Натуральные числа можно сравнивать, складывать, умножать.

Известное высказывание немецкого математика Леопольда Кронекера(1823-1891): «Бог создал натуральное число, всё остальное – дело рук человека…»

Обобщение множества N – множество Z целых чисел. Z состоят из N чисел, нуля(0) и отрицательных чисел. Целые числа можно сравнивать, складывать, умножать и вычитать. На множестве целых чисел разрешимо уравнение

(2). Желание решить уравнение вида (3) привело к появлению множества рациональных чисел. Рациональным числом называют число, представленное в виде

Рациональные числа можно складывать, умножать, вычитать, делить на число, не равное нулю(≠0). Таким образом имеет место выражение

Для описания многих процессов, происходящих в природе, недостаточно множества рациональных чисел.

Древнегреческий философ Зином используя понятие бесконечности и находясь в рамках рациональных чисел, доказывал, что быстрому Ахиллесу не догнать медленную черепаху.

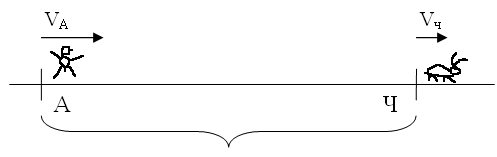
В начальный момент расстояние между Ахиллесом и черепахой равно S. Черепаха и Ахиллес двигаются в одном направлении.

Чтобы попасть в точку, где находится черепаха (точка Ч.), Ахиллесу необходимо время t₁, равное , а за это время черепаха уползёт на расстояние .

Чтобы пройти расстояние S₁, Ахиллесу потребуется время , а за это время черепаха уползёт на расстояние .

Этот цикл никогда не закончится и Зинам делает вывод, что Ахиллес никогда не догонит черепаху.

Подобным образом Зинам доказывал, что движение вообще не возможно описать только с помощью рациональных чисел.

Другой пример, показывающий недостаток рациональных чисел.

Согласно теореме Пифагора диагональ квадрата с единичной стороной равна .

Длина диагонали единичного квадрата не может быть выражена рациональным числом. Для доказательства этого утверждения предположим противное:

(4) ,

причем m и n – взаимно простые числа, то есть дробь несократима.

Заметим, что каждое нечётное число в виде , где k – некоторое нечетное число. Возведя нечётное число в квадрат, получим .

В результате получим нечетное число.

Возведя уравнение (4) в квадрат получим:

число m должно быть чётным т.к. m и n взаимно просты, а число n должно быть нечетным. Представим четное число m в виде: m=2k

Подставим эту величину в (5) получим, то должно вытекать что n - чётное; получили противоречие доказывающее, что k не является рациональным числом.

Наиболее естественным процессом для расширения множества рациональных чисел явление десятичных дробей; каждое рациональное число может быть представлено в виде конечной или бесконечной десятичной дроби, например .Таким образом, видим что рациональное число представима в виде бесконечно десятичной дроби. Известно, что бесконечная десятичная дробь выражает рациональное число тогда, когда она является периодической, т.е. с некоторого момента в десятичной записи числа, будет повторяться одинаковая группа цифр.

Зная представления рационального числа в виде бесконечной десятичной дроби, всегда можно получить представление этого числа в виде отличающихся двух чисел.

6,083131(31) =6+0,08+0,0031+0,000031+0,00000031+…

Замечаем, что, отбросив два первых слагаемых, получим сумму геометрических прогрессов.

6,08+31(0,0001+0,000001)

Поставим в соответствие каждой точки М числовой оси, некоторую вполне определенную десятичную дробь. Выберем на числовой оси начало отсчёта точку М и единичный отрезок OE.

С помощью OE определим длину отрезка ОМ с точностью до единицы. Для этого выясним, сколько раз отрезок ОЕ укладывается в отрезок ОМ.

Пусть ОЕ укладывается в ОМ раз при этом могут возникнуть два случае:

В первом случае после измерения ОМ, остаётся длина отрезка NM, которая меньше выбранного масштаба в этом случае является результатом измерения ОМ.

По недостатку с точностью до единиц, во втором случае, целое число а₀ может выражать длину всего отрезка ОМ. В этом случае отрезку ОМ можно поставить бесконечную десятичную дробь

Чтобы точнее измерить отрезок ОМ в первом случае, разбивают отрезок ОЕ на десять равных частей и рассматривают столько десятых частей ОЕ, сколько может уместиться в NM.

При этом также могут возникнуть Q случаев. Во втором случае величина отрезка ON будет определена . Переписав 000, получим бесконечную десятичную дробь.

В первом случае будет выражать длину ON по недостатку с точностью, повторяя аналогичные рассуждения, придём к двум возможностям:

а) процесс измерения оборвётся на n-ом шаге m N будет поставлена в соответствии будут поставлены рациональные числа .

б) описанный процесс никогда не оборвётся и мы получим последовательность рациональных чисел.

Элементарные последовательности представляют собой результат измерений по недостатку отрезка ОМ.

В этом случае m M вполне определенная бесконечная десятичная дробь

Из приведённого рассмотрения корень может быть представлен в виде бесконечной десятичной дроби.

Определение: Числа, представленные в виде десятичных дробей, принято называть действительными(вещественными) числами.

Множество вещественных чисел обозначают буквой R.

Приведённые расстояния показывают, что координатам R ставится в соответствии некоторый бесконечный процесс, называемый предельным переходом.

Для R операции сравнения, сложения, умножения. Вычитания и деления выводятся исходя из идей представления чисел рациональными числами с любой неопределённой заданной погрешностью. Например, суммой x вещественных чисел называют R x, которое для любых вещественных чисел , удовлетворяющих неравенству

, удовлетворяют неравенству , при этом .

В более полном курс математики доказывается, что подобным образом определённые операции удовлетворяют аксиомам справедливости рациональных чисел.

Множество R является полным, то есть нельзя построить более широкое множество с теми же правилами и свойствами.

Таким образом для числовых множеств справедливо

Множество R принято обозначать числа, входящие в это множество называются его элементами или точками.

Определение: Множество вещественных чисел {х} называется ограниченным сверху(снизу), если существуют такие вещественные числа что для всех элементов множества х будет выполняться неравенство . При этом числа называют верхней (нижней) гранью множества.

Определение: Наименьшая из всех верхних граней, ограниченного сверху множества х, называют точной верхней гранью этого множества и обозначают в виде

Supremum – наивысшее

Наибольшая из всех нижних граней, ограниченного снизу множества х, называют точкой нижней грани и обозначают в виде:

Infimum – наинизшее

Теорема: Если множество вещественных чисел R содержит хотя бы один элемент и ограничено сверху(снизу), то у этого множества существует точки верхней(нижней) грань.

Определение: Интервал, где q>0 называется эпсилон-окресностью точки а.(q принимать за ε)