Свойства числа сочетаний

Из формулы (1) для числа сочетаний вытекает 2 свойства числа сочетаний:

1. =

2. +

Из формулы (1) с учетом того, что 0! = 1 вытекает, что = .

С учетом сделанного замечания, второе свойство позволяет вычислять число сочетаний с помощью треугольника Паскаля.

Число сочетаний также называется биноминальным коэффициентом.

Рассмотрим формулы, позволяющие возводить в степень (a+b):

Сравнивая коэффициенты в правых частях с треугольником Паскаля, замечаем, что коэффициенты правых частей совпадают с соответствующими числами треугольника Паскаля.

С помощью метода математической индукции можно доказать формулу:

(2)

Соотношение (2) называется биномом Ньютона; откуда вытекает второе название числа сочетаний – биноминальный коэффициент.

Определение: Преобразование перестановки, которое меняет местами какие-либо два символа, а все остальные символы оставляет на своих местах называется транспозицией.

Определение: Два числа i , j образуют в перестановке инверсию, если i > j , и i стоит в перестановке раньше j.

Пример:

Подсчитать число инверсий в перестановке 32145.

1-ца образует две инверсии, 2-ка образует одну инверсию.

2 + 1 + 0 + 0 + 0 = 3 инверсии.

Сделаем в нашей перестановке транспозицию (поменяем местами 1 и 5). Посчитаем число инверсий.

3 2 5 4 1

4 + 1 + 0 + 1 + 0 = 6 инверсий

Определение: Перестановка называется четной, если число инверсий в ней определено четным числом, нечетная в обратном случае.

Теорема: Каждая транспозиция меняет четность в перестановке.

Определение: Всякое взаимнооднозначное отображения первых n – натуральных чисел на себя называется подстановкой n – го порядка.

Каждую подстановку n – го порядка можно записать с помощью 2 -х перестановок.

В такой записи подчеркивается что три переходит в четыре 3-4, 2-3, 1-2, 4-5, 5-1.Одну и ту же подстановку можно записать различными способами :

1)поменяв в подстановке какие-либо столбцы

При такой записи видим, что число различных подстановок определяется нижней строкой, т.е. числом различных перестановок, следовательно число различных подстановок n-го порядка равного n!.

Подстановка называется четной, если сумма числа инверсий обоих ее перестановок является четным числом и нечетной в противном случае. Отметим , что выполнив в подстановке транспозицию столбцов не изменяим ее четности.

Определитель n-го порядка.

Определитель 2 и 3 порядка вычисляется по следующим формулам.

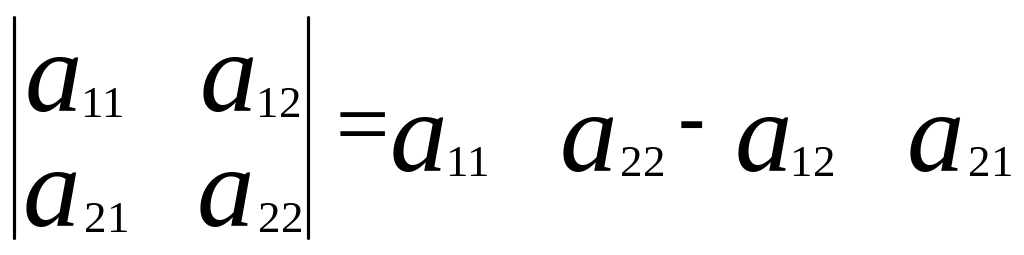
Для того чтобы обобщить понятия определителей 2 и 3 – го порядка на случай определителя n – го порядка рассмотрим вспомогательную задачу .

Пример:

Сколькими способами на шахматной доске можно расставить ладьи , чтобы они не били друг друга.

1
2
3
4
5
6
7
8
0	1	2	3	4	5	6	7	8

Замечаем что каждому расположению ладей на шахматной доске соответствовать подстановке 8-го порядка.

Число различных подстановок 8-го порядка. Число различных перестановок 8!=1*2*3*4*5*6*7*8=40320. Рассмотрим шахмотную доску 2*2:

1) 2)

II				II
	II		II

1) 1 2 2) 1 2

1 2 2 1

Две ладьи можно расположить двумя способами:

-в первом случае перестановка чётная 1 инверсия.

-во втором не чётная. Заметим, что расположение ладей соответствует образованию слагаемых в определителе второго порядка. Если чётная подстановка, то берётся «+», если не чётная, то «-».

Рассмотрим теперь шахматную доску размера 3*3. Три ладьи можно расположить 6-и способами.

II

II

II

II

II

II

II

II

II

II

II

II

II

II

II

II

II

II

Видим, что каждому расположению ладей, соответствует расположение множителей в слагаемых определителя 3-го порядка.

Определителю n-порядка соответствует квадратная матрица А называется число равное сумме n! слагаемых, каждое из которых определяется подстановкой n-ой степени,

причём слагаемое берётся со знаком «+» если подстановка

чётная,и со знаком «-» если не чётная.

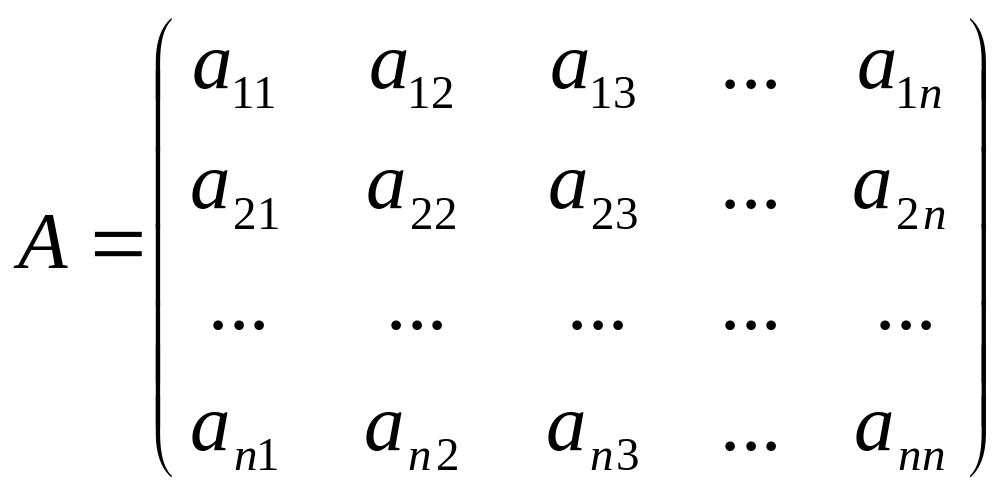
Определитель n-го порядка принято записывать =detA=

-число инверсий в подстановке

Свойства определителя.

Определение: При образовании матрицы, при которой её строки становятся столбцами,с теми же номерами,называется транспонированием матрицы.

Транспонируем матрицу А:

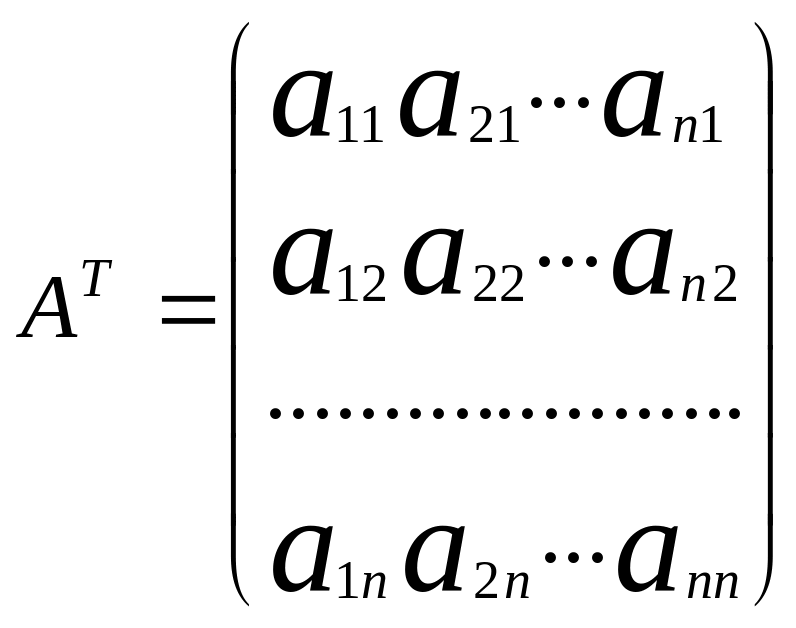
Свойство1: Определитель не меняется при транспонировании.

Доказательство: Пусть слагаемые входят в состав определителя А.Это же слагаемое будет входить в состав определителя ,в определителе А знак слагаемого определяется подстановкой ,а в определителе -подстановкой . Видим, что обе подстановки обладают одинаковым числом инверсий, следовательно, определители матрицы и матрицы состоят из одних и тех же слагаемых, взятых с одинаковыми знаками.

Из первого свойства вытекает, что всякое утверждение о строках определителя годится и для его столбцов.

Свойство2: Если определитель содержит нулевую строку, то он равен нулю.

Доказательство: в каждом слагаемом определителя будет присутствовать множитель из нулевой строки, следовательно, все слагаемые равны нулю, и определитель равен нулю.

Свойство3: Если в определители поменять местами две строки, то определитель сменит знак.

Доказательство: пусть в определителе n-го порядка, меняются местами i и j строки. Слагаемые исходного определителя вида (4) имеет знак определяемый подстановкой (4), , поменяв местами i и j строки получим тоже слагаемое, знак которого будет определяться подстановкой , видим, что выполненные подстановки имеют противоположенную чётность, следовательно, заменив местами i и j строки, сменим знаки у всех слагаемых, в результате чего определитель сменит знак.

Свойство4: Если определитель содержит две одинаковые строки, то он равен нулю.

Доказательство: пусть определитель равен d, поменяв местами одинаковые строки,получим определитель -d, так как меняем одинаковые строки, то на самом деле определитель не должен измениться d=-d 2d=0 d=0.

Свойство5: Если все элементы некоторой строки определителя умножить на число k, то сам определитель умножится на число k.

Доказательство: пусть на k умножатся все элементы i-ой строки, так как в каждом слагаемом присутствует множитель из i-ой строки, то при умножении i-ой строки на число k, то каждое слагаемое приобретёт множитель k следовательно весь определитель умножится на k.

Свойство6: Если в определители нет пропорциональной строки, то определитель равен нулю

.

Доказательство: доказательство вытекает из 5 и 4 свойств определителя.

Свойство7: Если в определители элементы i-ой строки представляют собой сумму двух чисел, то определитель равен сумме двух определителей, все элементы которых кроме элементов i-ой строки такие элементы , как и в исходном определителе, а элементы i-строки в первом определителе состоят из 1-ых слагаемых, а во втором определителе из вторых слагаемых

(1)

Доказательство: Рассмотрим произвольное слагаемое определителя

Используя представление (1), выписанное слагаемое, можем записать в виде:

Воспользовавшись дистрибьютивностью,

получим слагаемые:

Применив эту операцию к каждому слагаемому определителя и ,сгруппировав отдельно 1 и 2-ое слагаемое, получим сумму двух определителей, указанных в свойствах.

Свойство8: Если одна из строк определителя равна линейной комбинации остальных строк, то определитель равен 0.

Доказательство выражается из 7 и 6 свойств.

Свойство9: Определитель не изменится, если к элементам его строки прибавить соответствующие элементы его другой строки, умноженное на некоторое число.

Доказательство выражается из 7 и 8 свойств.

Определение: Минором k-того порядка называется определитель k-того порядка, получаемый из определителя порядка n(n>k) вычеркиваем (n-k) строк и (n-k) столбцов.

Определение: Дополнительным минором к заданному минору k-того порядка называется определитель порядка (n-k), получаемый из определителя порядка n, вычеркиваем k-строк и k-столбцов, в которых расположен исходный минор.

Пусть M некоторый минор k-того порядка, M`-его дополнительный минор.

Определение: Алгебраическим дополнением к минору M называется A=(-1)^SM`(выражение), где S- сумма номеров строк и номеров столбцов, в которых расположен минор M.

Пример: рассмотрим определитель 7-го порядка.

Выписываем минор 3-го порядка, расположенной во 2,5,7 строке и в 1,4,6 столбце.

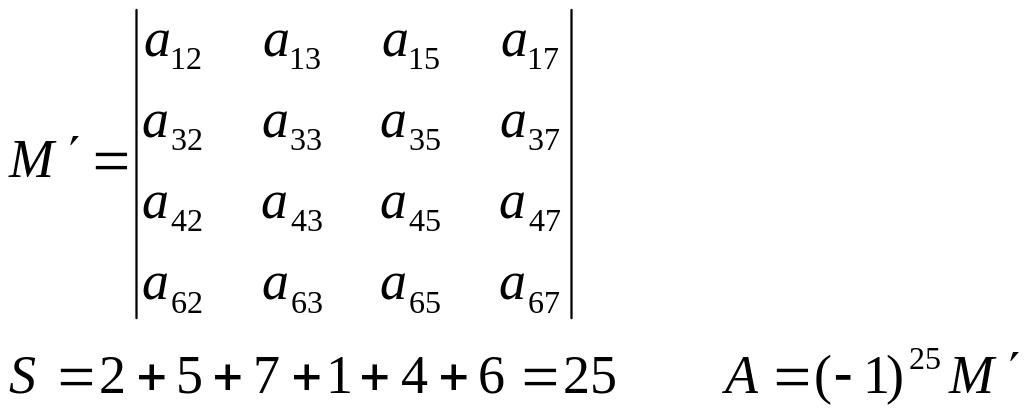
Теорема: Произведение минора М на его алгебраическое дополнения состоит из слагаемых, которые являются слагаемыми в исходном определителе n-го порядка с теми же самыми знаками.