Метод Крамера. Определитель второго и третьего порядков.

Рассмотрим определенную систему двух уравнений содержащую две переменные

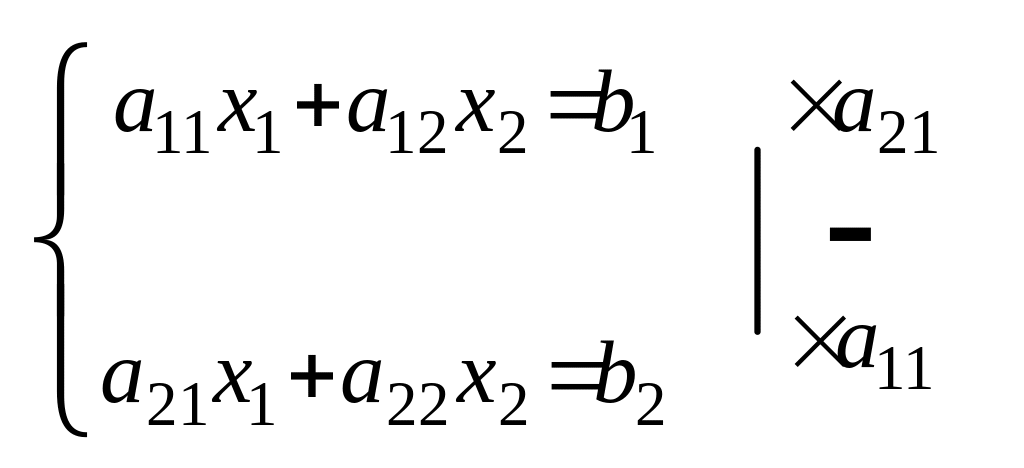(1)

Для определённости будем считать что коэффициент .Преобразуем систему (1),умножив второе уравнение системы на и вычтем из него первое уравнения на . В результате получается эквивалентная система вида.

Поскольку рассматриваем определённую систему, то коэффициент при во втором уравнении отличен от нуля и переменную можно представить в виде:

Подставим найденное значение в первое уравнение:

Представление (2) значений , выраженные через коэффициенты и свободные члены системы (1), принято называть нахождением решений системы(1) по методу Крамера. Числители и знаменатели соотношений(2) принято записывать в виде прямоугольной таблицы:

Такая комбинация четырёх чисел называется определителем второго порядка. Чтобы вычислить определитель второго порядка, нужно перемножить элементы, стоящие на главной диагонали, и отнять от полученных величины произведения элементов, стоящих на побочной диагонали. Знаменатель представления (2) также может быть записан в виде определителя второго порядка:

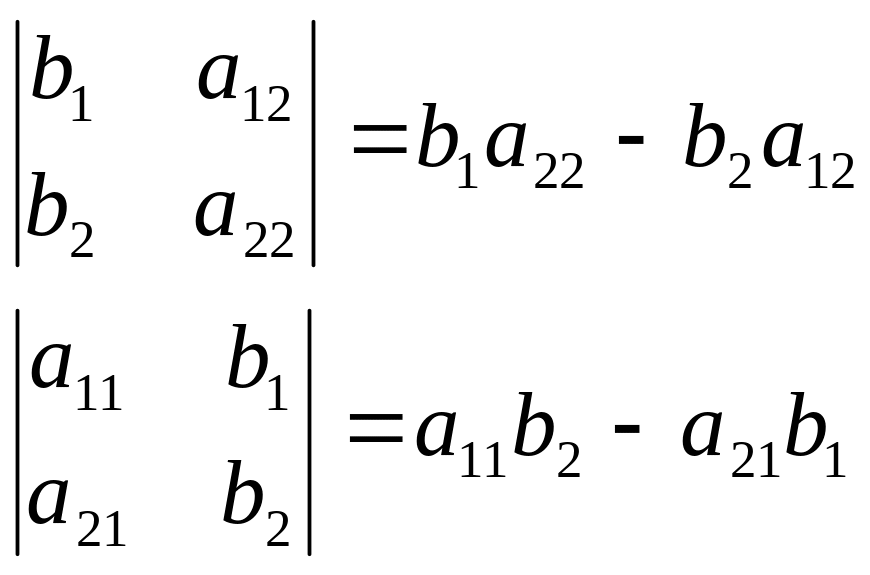
Решение системы можно представить в виде:

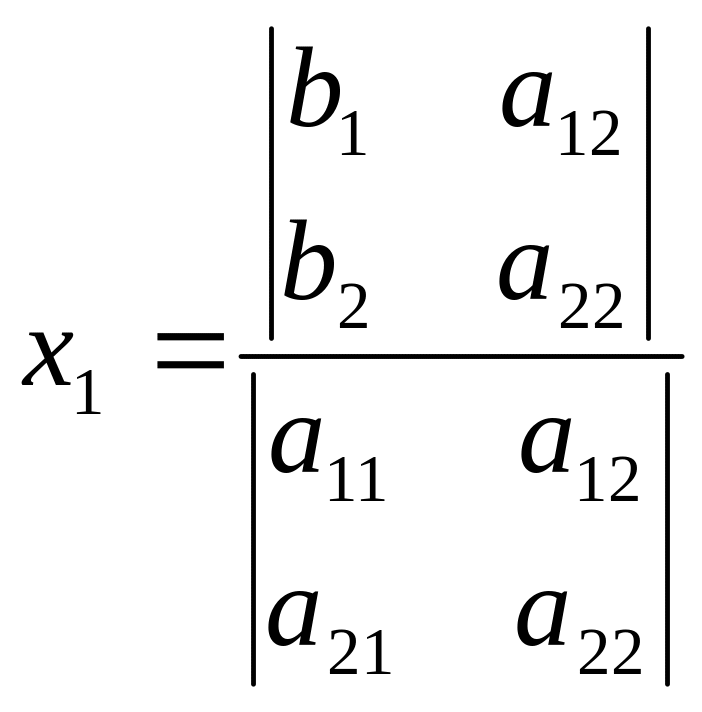
Получение решений по формулам (3) называется методом Крамера. Решение определенных систем линейных уравнений 2-го порядка. Проведя аналогичное рассмотрение для определенных систем 3-го порядка:

(4)

Получим представление решения системы в виде

(5)

Число, записанное в виде прямоугольной таблицы, состоящее из девяти чисел, называется определителем 3-го порядка.

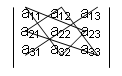
Слагаемые в определителе третьего порядка со знаком «+» и «-» образуется из элементов определителя согласно схеме.

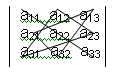
Получение решения по формулам (5) так же называется методом Крамера решения определенных систем уравнений третьего порядка. Определители второго и третьего порядка были определены, исходя из решения системы линейных уравнений. Очевидно, что такой подход не годится для определения определителя n-го порядка! Чтобы ввести понятие определителя n-го порядка, рассмотрим некоторые понятия комбиноторики.

Элементы комбинаторики.

Пусть М – произвольное множество, состоящее из n элементов(|M| = n). Поскольку все элементы множества М можно занумеровать, то в дальнейшем, вместо множества, состоящего из конечного числа элементов, будем рассматривать числовые множества, состоящие из первых n чисел натурального ряда.

Определение: Размещением из n элементов по p в каждом называются такие комбинации, состоящие из p элементов, которые отличаются друг от друга либо самими элементами, либо порядком их расположения.

Принято различать размещение с повторениями и размещением без повторений. Очевидно, что размещения с повторениями совпадают с упорядоченным набором р-элементов, выбираемых из множества n-элементов. (а₁,а₂, а₃, … , а_n). n^p – число размещений с повторениями; число размещений без повторений A и равно произведению . Поскольку в этом случае первый элемент а₁ выбирается из множества n-элементов, второй а₂ выбирается из элементов, последний из элементов. Частным случаем размещения является перестановка.

Определение: Любое расположение первых n-натуральных чисел называется перестановкой.

Число перестановок обозначается P_n= 3*2*1*=n! (!– факториал)

0!=0

1!=1

2!=1*2=2

3!=1*2*3=6

4!=1*2*3*4=24

С учетом понятия факториала можно представить в виде

Определение: Сочетаниями из n-элементов по р в каждом называют такие комбинации р-элементов, которые выбираются из множества n-элементов без повторений, причем порядок расположения элементов не имеет значения.

- число сочетаний.

Рассмотрим комбинацию из (a,b,c) элементов. Выпишем всевозможные комбинации этих элементов с учетом порядка (a,b,c) (b,a,c) (c,a,b) (a,c,b) (b,c,a) (c,b,a). Таким образом получили 6 комбинаций, называемых размещениями без повторений.

С точки зрения сочетания в этом случае речь идет об одной комбинации. Упорядочив каждое сочетание, получим все множество размещений. Каждое сочетание, состоящее из p-элементов можно упорядочить, превратив в p! Размещений. Таким образом, отсюда вытекает, что число сочетаний

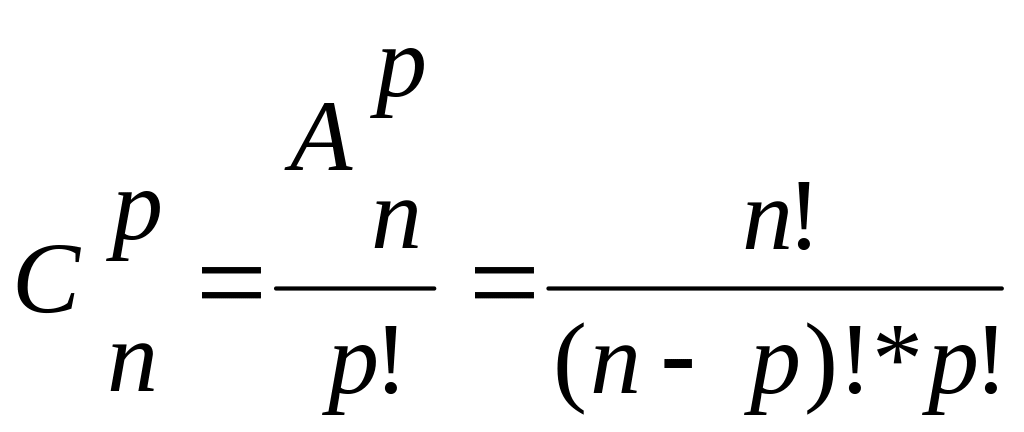
Пример:

Какое количество символов можно закодировать с помощью 1 байта?

1 байт=8 бит. В каждом бите можно записать либо 1 либо 0. Речь идет об упорядоченной 8-ке из 2-х элементов или другими словами о размещениями с повторениями.

n^p=2⁸=256

Пример:

Сколькими способами можно выбрать трех человек на три разные должности из числа 10 претендентов.

Поскольку должности различны, речь в задаче идет о размещении из 10 по 3.

= = = 720 (комбинаций)

Пример:

Сколькими способами можно выбрать трёх человек на три одинаковые должности из числа 10 претендентов.

Речь идет о сочетаниях. Число различных сочетаний будет равно:

= = = 120