Метод Гаусса . Решение систем линейных уравнений.
Рассмотрим систему линейных уравнений :
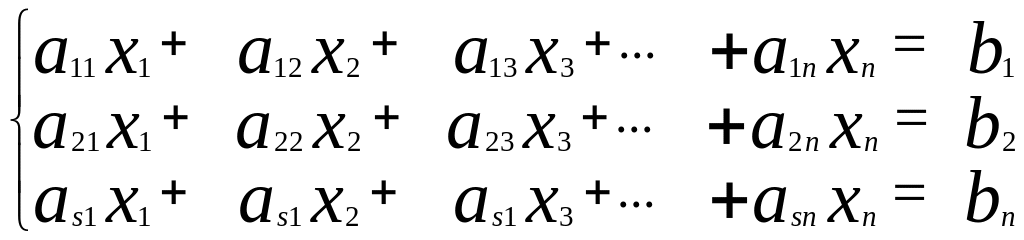(1)
Отметим что в системе (1) присутствует S – уравнений и n неизвестных. Натуральные числа S,n ни не связаны друг с другом.
,
-
некоторые числа в дальнейшем, если не
оговорено противное, будем предполагать
эти числа вещественными.
– неизвестная переменная. Совокупность
неизвестных элементов (
,
…
)
можно рассматривать как упорядоченный
n
мерный вектор (
,
…
).
При исследовании системы (1) рассматривают прямоугольную таблицу коэффициентов, называемую матрицей (А).
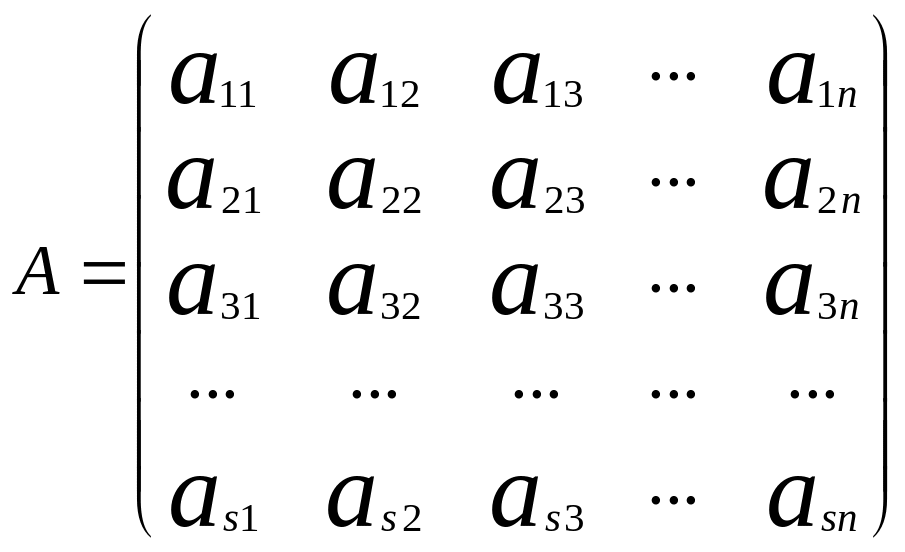(2)
Принято говорить ,что матрица (2) имеет размеры S*n . Добавление к матрице А столбца свободных членов приводит к новой матрице , которую принято называть расширенной матрицей.
Часто, чтобы показать особенность последнего столбца его отделяют вспомогательной черточкой.
Определение: Упорядоченную
совокупность чисел (
,
…
)=
(n
мерный вектор
) называется решением системы (1) ,если
подстановка вместо вектора
вектор
обращает
каждое уравнение системы (1) в тождество.
Определение: Система уравнений называется совместной, если она обладает решением, и несовместной, если она не обладает решением. Совместная система называется определенной, если решение единственно и неопределенной, если решений бесконечное множество.
Определение: Две системы линейных уравнений называются эквивалентными (равносильными), если они обе несовместны или обе совместны и обладают одинаковыми наборами решений.
Определение: преобразование системы (1) вида:
а)перемена местами уравнения системы.
б)умножение уравнения системы на число отличное от нуля.
в)прибавление к одному уравнению системы другого уравнения, умноженного на некоторое число отличного от нуля - называются элементарными.
Покажем, что элементарные преобразования не выводят за пределы классов эквивалента. Для преобразований типа пункт а) и б) это очевидно.
Докажем это утверждение для преобразования
в). Для определённости, умножим первое
уравнение системы (1) на число
,
и вычтем его из второго уравнения, в
результате придём к системе уравнению
вида:
+
+…+
=
+…+
=
…………………………………. (3)
где,
Введём новые обозначения: левую часть
первого уравнения системы (1) обозначим
символом
Левую часть второго уравнения системы
(1) обозначим:
Левую часть второго уравнения системы
(3) обозначим
=
Согласно новым обозначениям второе уравнение системы (3) можно представить в виде:
Пусть вектор k является
решением системы (1).Это означает, в
частности что
=
и
Очевидно, что все уравнения системы
(3),кроме второго, совпадают с соответствующими
уравнениями системы (1), так как необходимо
показать, что вектор
является решением второго уравнения
системы (3).
Показали, что каждое решение системы
(1) является решением системы (3).Докажем
подобное утверждение в обратную сторону.
Пусть вектор
=
является
решением системы (3).Нужно показать, что
этот вектор является решением системы
(1).
И для доказательства достаточно
рассмотреть второе уравнение системы
(1).Заметим, что второе уравнение системы
(1) можно представить в виде:
.
Т.к. вектор
является
решением системы (3),то
.
Подставим во второе уравнение системы
(1) вектор
,получим
=
=
Таким образом показали,
что преобразования в,
также не выводят за пределы класса
эквивалентности. Покажем процедуру,
позволяющую находить простейшие
представители класса эквивалентности.
Пусть
,
этого всегда можно добиться перенумеровав
в случае необходимости порядок переменных
в уравнениях системы. Перейдём от системы
(1) к системе (4), заменив i-ое
уравнение при i>1,
линейной комбинацией i-ого
и первого уравнения умноженного на
коэффициент
,
Заметим, что в левой части i-ого уравнения, после указанного преобразования будет отсутствовать переменная , таким образом, система (4) примет вид:
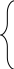
(4)
- - - - - - - - - - - - - - - - - - - -
Рассматривая подсистему системы (4), без первого уравнения, применили к ней рассмотренную выше процедуру (оставим переменную только в первом уравнении подсистемы, и уберем её из остальных уравнений). Применяя аналогичную процедуру необходимое число раз, найдем канонический вид системы (1), при этом могут возникнуть три случая:
1. В процессе элементарных
преобразований может получиться
уравнение, в правой части которого стоит
число
,
а все коэффициенты при неизвестных в
левой части равны нулю. Получим уравнение
вида
,
в этом случае говорим, что подобное
соотношение невозможно и система не
имеет решений.
2. Во втором случае исходная система приводится к треугольному виду:
- - - - - - - - - - - - - -
Переменную
находят из последнего уравнения системы,
подставляя, найденное значение
в предпоследнее уравнение, находят
неизвестную
,
поднимаясь, таким образом, находят
единственное решение системы уравнений,
в этом случае система совместная и
определенная. Система приводится к виду
трапеции:
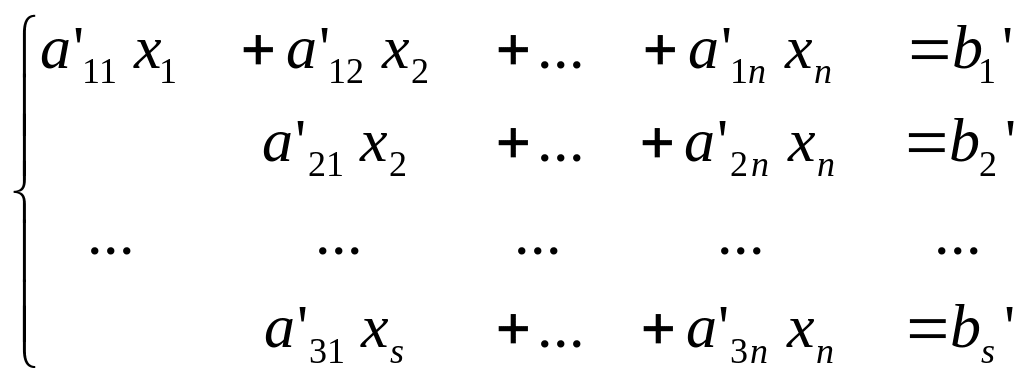
В этом случае переменные
разделяются. Переменные
,
образующие треугольник, остаются в
левой части, оставшиеся переменные
,
объявляются свободными параметрами, и
переносятся в правую часть уравнения.
Решение в этом случае будет зависеть
от n-m-параметров.
Такое решение называется общим решением
системы. Придавая параметрам конкретные
числовые значения, получим частное
решение. Система в этом случае называется
совместной и неопределенной.
Пример:
а) рассмотрим систему
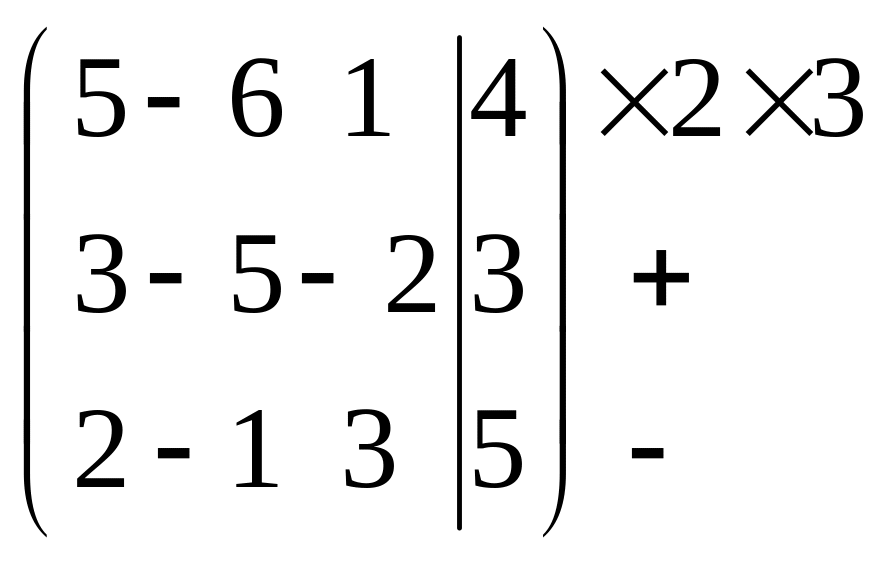
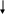
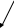
В нашей системе легче начать с переменной, коэффициент которой равен 1.
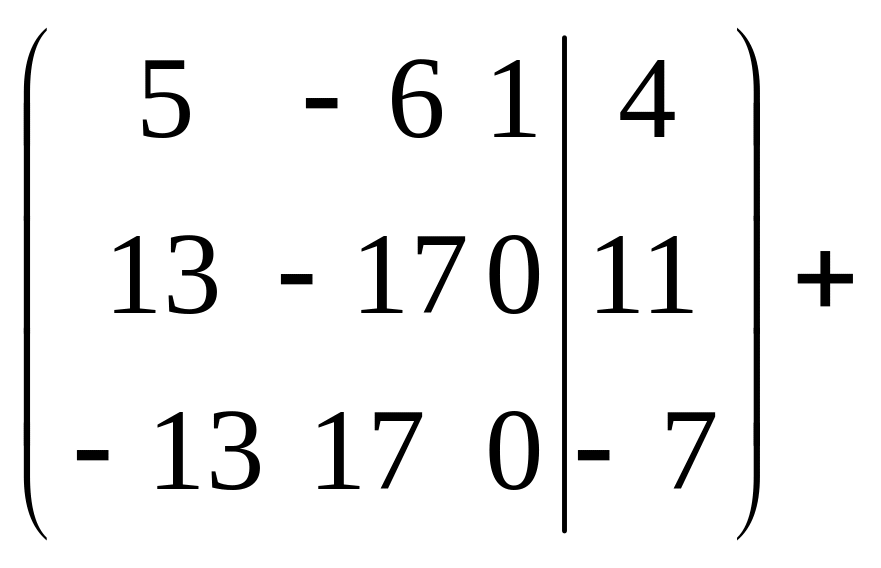
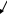
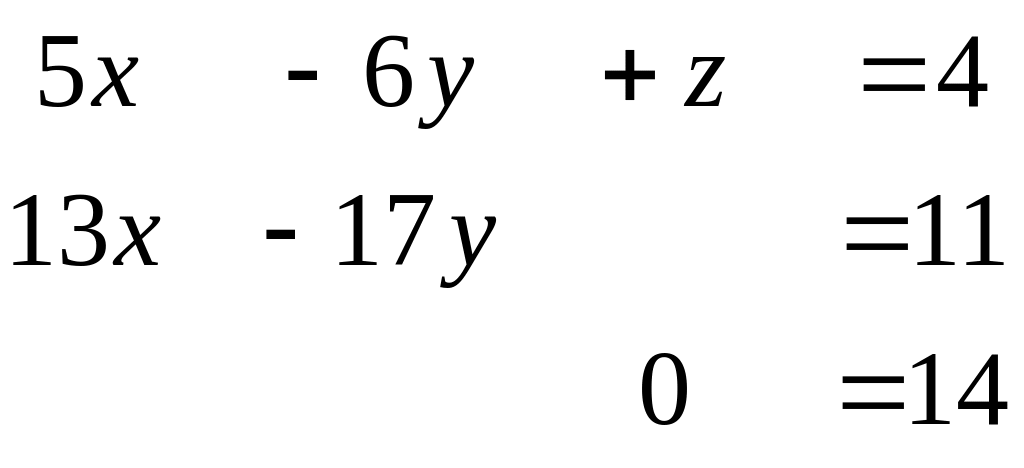Система не совместна.
Дадим геометрическую интерпретацию рассмотренной системе. Из школьного курса известно, что каждое уравнение системы определяет плоскость в пространстве x,y,z. Мы имеем 3 непересекающихся плоскости. Данной системе может соответствовать следующее расположение плоскостей:
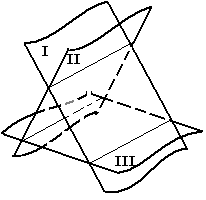
в)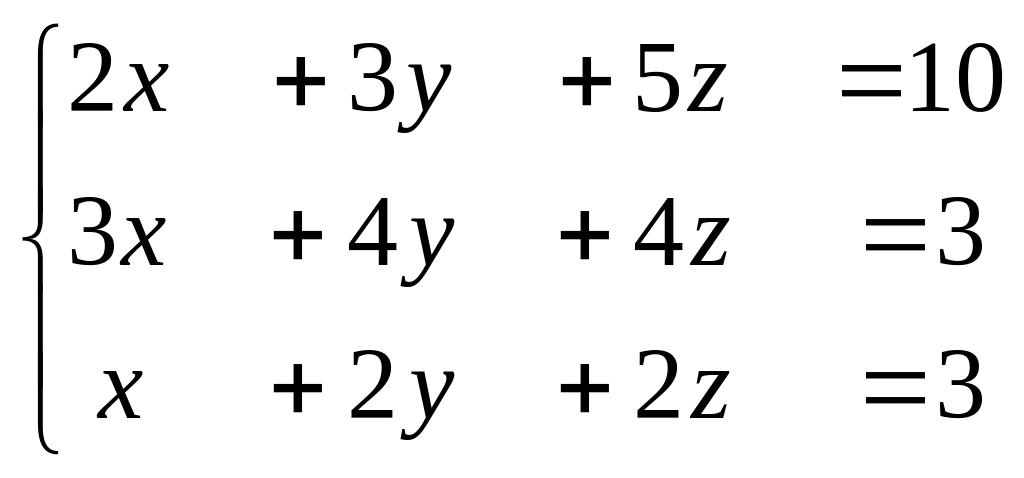
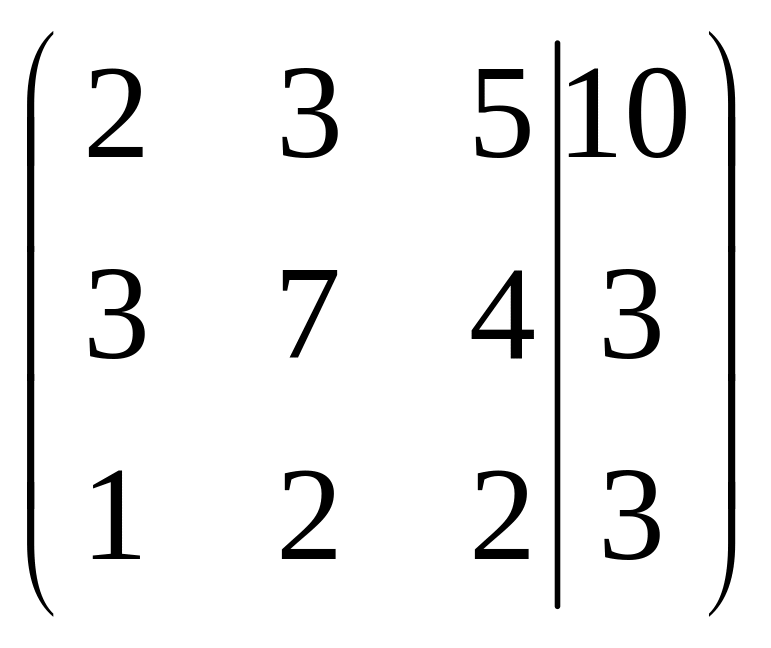
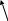
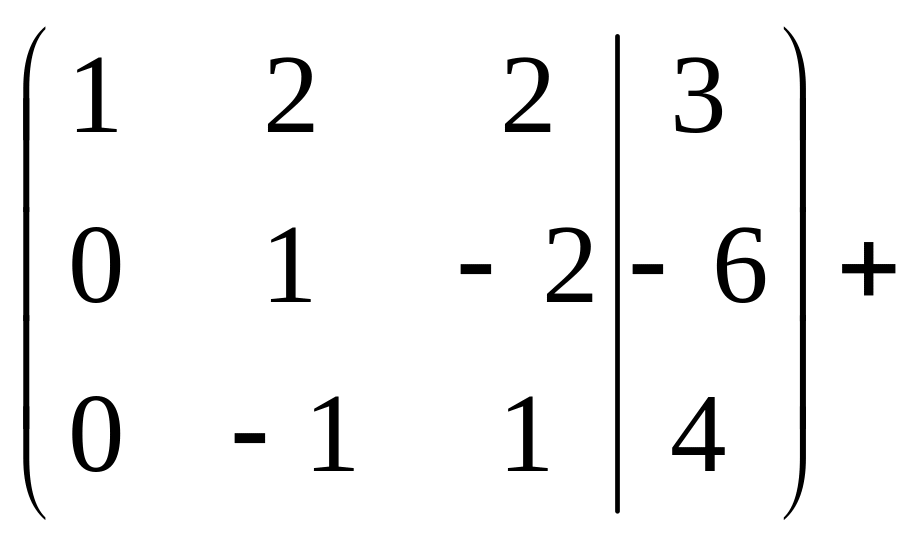
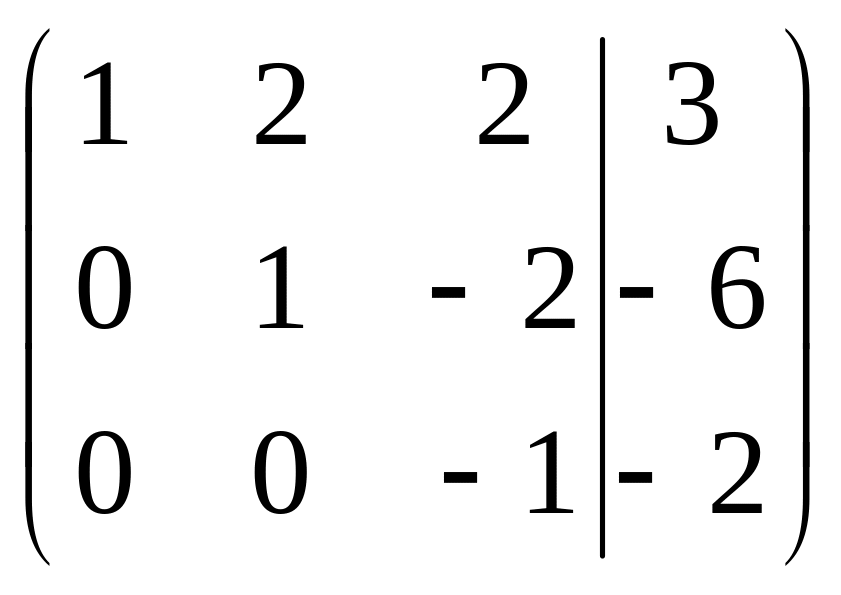
Эта система совместная и определенная. Эквивалентная система имеет вид:
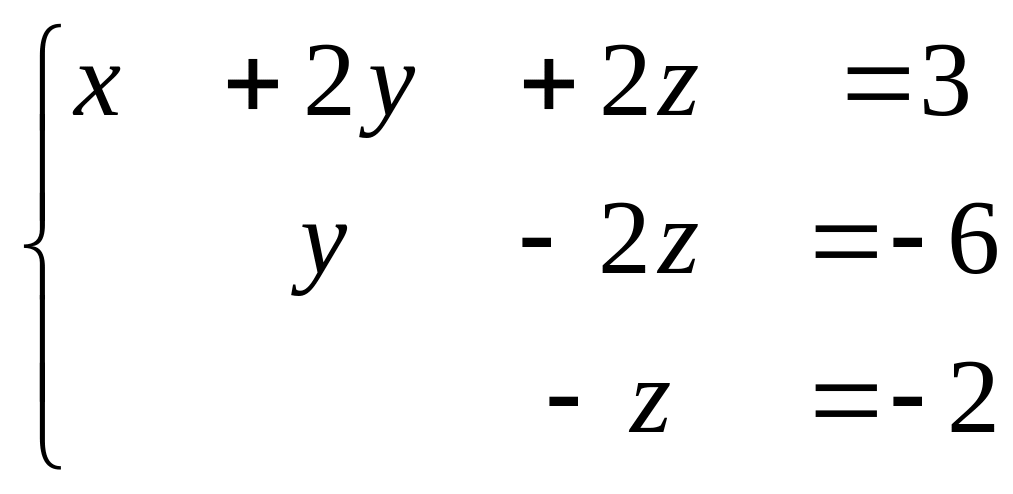
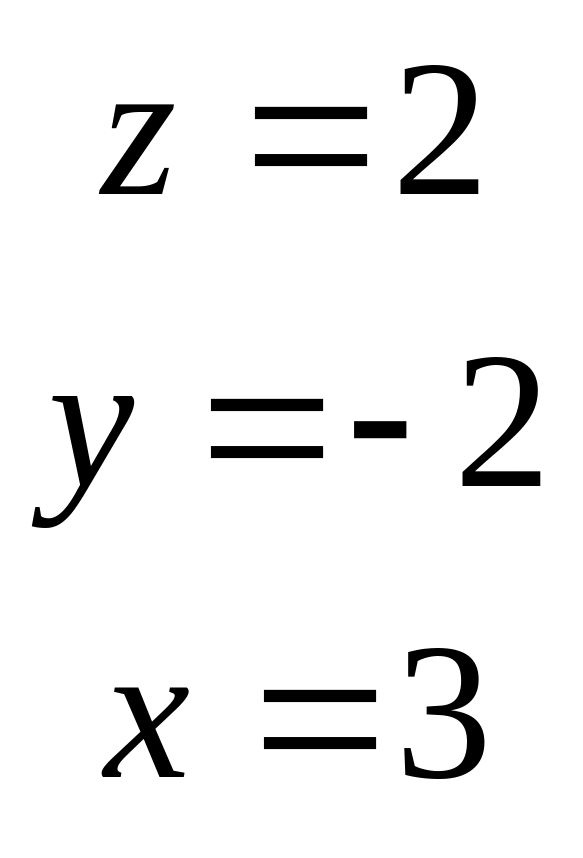
Геометрически это означает, что 3 плоскости пересекаются в одной точке.
с)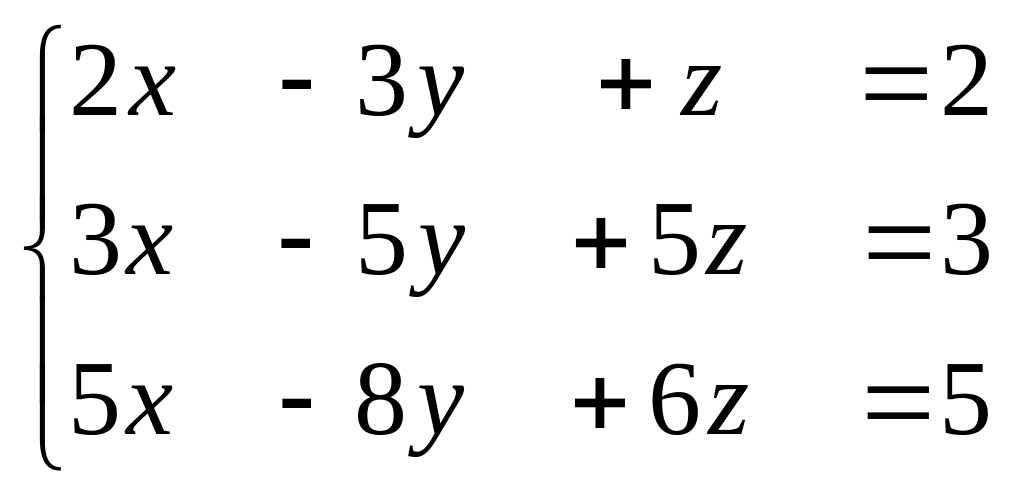
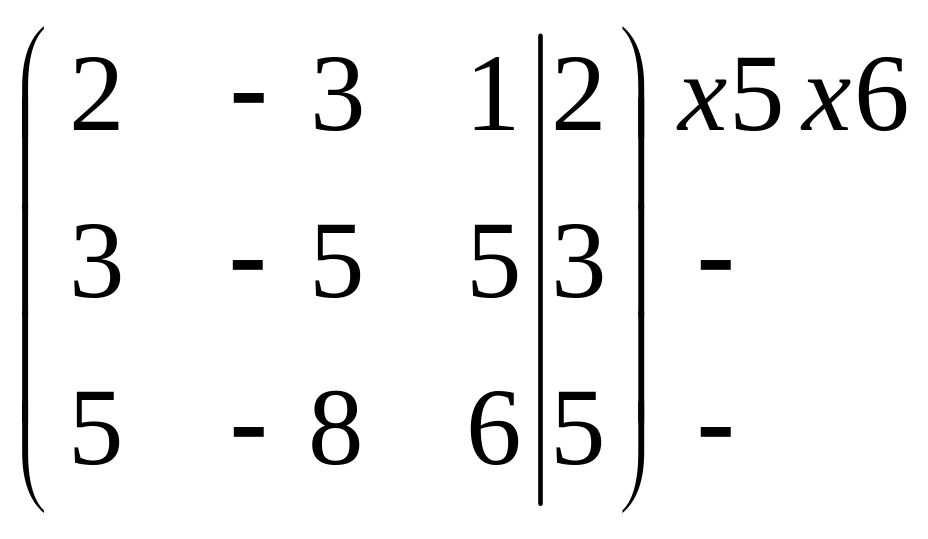
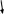
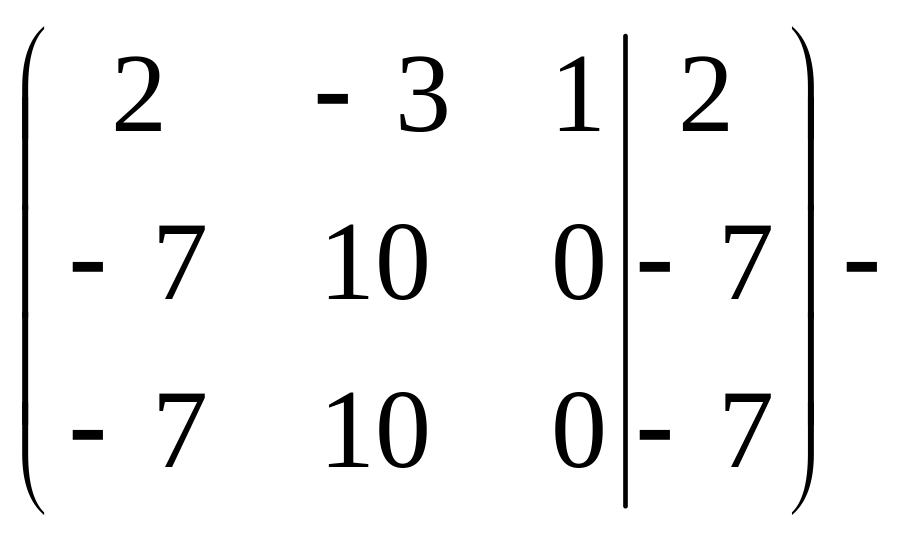
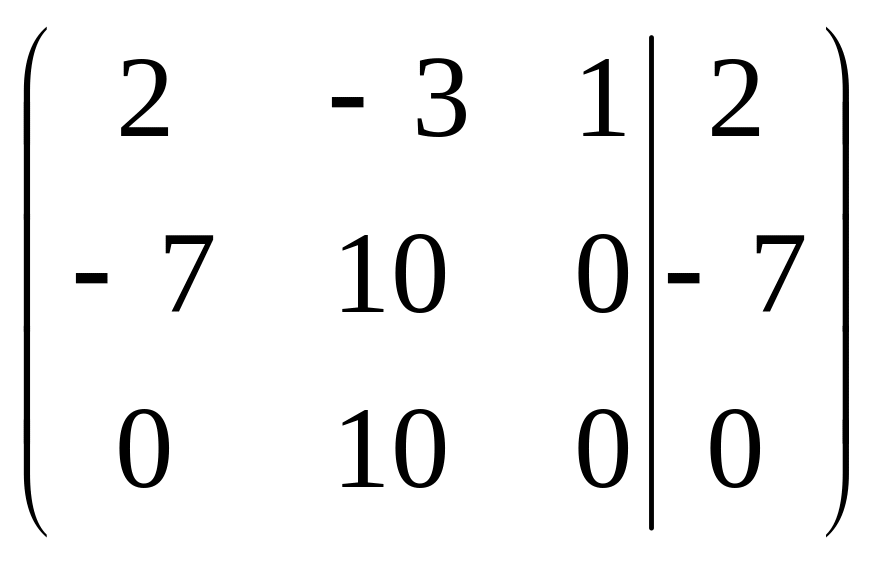
Матрица вида трапеции.
пусть x=t
,
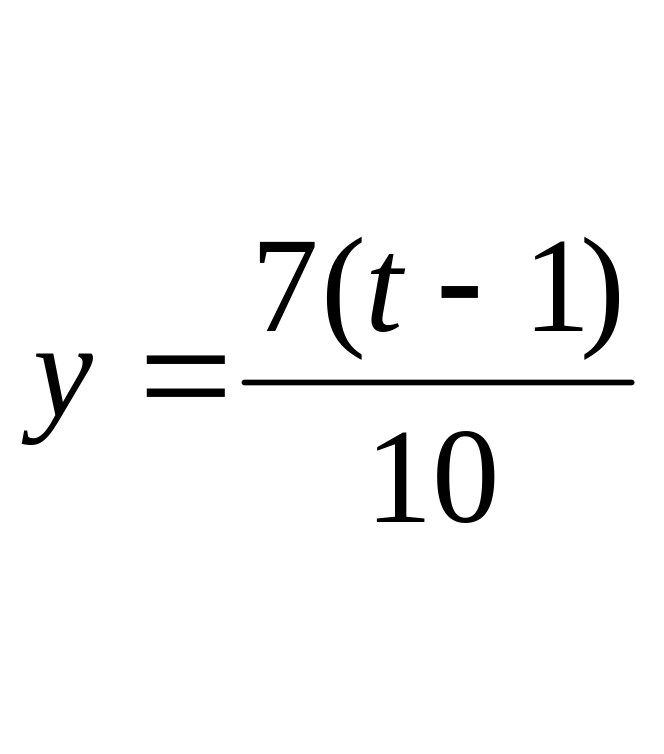
Решение такого типа называется, общим решением →система совместна и неопределенна. Геометрически это означает, что множество решений этой системы образуют некоторую прямую, являющуюся линией пересечения трех плоскостей.
