
- •Отношение эквивалентности
- •Свойства бинарных отношений
- •Метод Гаусса . Решение систем линейных уравнений.
- •Метод Крамера. Определитель второго и третьего порядков.
- •Элементы комбинаторики.
- •Свойства числа сочетаний
- •Определитель n-го порядка.
- •Разложение определителя по строке (столбцу).
- •Правило Крамера
- •Следствия из теоремы.
- •Решение матричных уравнений
- •Комплексные числа
- •Алгебраические операции над комплексными числами.
- •Линейные пространства
- •Линейная зависимость векторов .
- •Базис. Размерность.
- •Ранг матрицы
- •Матрица перехода
- •Система линейных уравнений
- •Теорема Кронекера - Капели
- •Система линейных однородных уравнений
- •Система однородных уравнений.
- •Линейные преобразования
- •Евклидово пространство
- •Свойства скалярного произведения
- •Процесс ортоганизации.
- •Векторная алгебра.
- •Скалярное произведение векторов в ортогональном базисе.
- •Двойное векторное произведение
- •Уравнение прямой и плоскости
- •Уравнение плоскости
- •Некоторые задачи о прямых и плоскостях.
- •Уравнение плоскости, проходящее через три заданных числа.
- •Расстояние от точки a до плоскости.
- •Расстояние от точки до прямой.
- •Расстояние между непараллельными прямыми в пространстве.
- •Кривые второго порядка
- •Уравнение касательной к эллипсу
- •Гипербола
- •Парабола
- •Поверхность второго порядка
- •Поверхности вращения
- •Эллипсоид
- •Конус второго порядка
- •Однополостный гиперболоид
- •Двуполостный гиперболоид
- •Эллиптический параболоид
- •Гиперболический параболоид
- •Математический анализ
- •Абсолютная величина u ее свойства
- •Последовательности.
- •Основные свойства бесконечно малых последовательностей.
- •Сходящиеся последовательности .
- •Монотонные последовательности.
- •Число е
- •Функция
- •Предел функции.
- •Непрерывные функции.
- •Классификация точек разрыва функции Точка устранимого разрыва.
- •Разрыв первого рода (конечный скачок)
- •Разрыв второго рода.
Разрыв второго рода.
Определение:
Точка
а называется точкой разрыва второго
рода для функции
![]() ,
если в этой точке функция
,
если в этой точке функция![]() не имеет хотя бы одного из односторонних
пределов, либо хотя бы из односторонних
пределов бесконечен.
не имеет хотя бы одного из односторонних
пределов, либо хотя бы из односторонних
пределов бесконечен.
Пример1. y = tg x
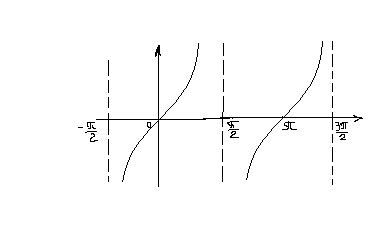
Из построенного графика
функции и из периодичности функции tg
x
следует, что значения аргумента функции
раны x
=
![]() ,
являются точками разрыва 2-ого рода.
,
являются точками разрыва 2-ого рода.
В т.
![]() имеет левый предел =
имеет левый предел =
![]()
Правый предел =![]()
Пример2. y
= sin
![]()
Покажем, что передел этой функции в 0 не существует. Для этого рассмотрим последовательность значений аргумента:
![]()
Видим, что эта последовательность сходится к 0.
Соответствующая последовательность значений функции
1;0;-1;0;1;-1;…;1;0;-1;…
Очевидно, что записанная
последовательность не является
сходящейся, т.к , например, для
положительного числа
![]() не существует такого номера N,
что при всех n
N,
значения последовательности
лежали бы в
-окрестности некоторого вещественного
числа.
не существует такого номера N,
что при всех n
N,
значения последовательности
лежали бы в
-окрестности некоторого вещественного
числа.
Таким образом, приведенная функция имеет в 0 разрыв второго рода.
Определение:
Функция
называется кусочно-непрерывной на
отрезке [![]() ]
, если она определена во всех точках
этого отрезка на сегменте [a,b]
и непрерывна за исключением конечного
их числа, в которых функция может терпеть
разрывы
1-ого
рода (конечные скачки), и кроме того
функция
должна обладать правым конечным пределом
в точке
, и левым конечным пределом в точке
]
, если она определена во всех точках
этого отрезка на сегменте [a,b]
и непрерывна за исключением конечного
их числа, в которых функция может терпеть
разрывы
1-ого
рода (конечные скачки), и кроме того
функция
должна обладать правым конечным пределом
в точке
, и левым конечным пределом в точке
![]() .
.
Функция называется кусочно-непрерывной на интервале, если она является кусочно-непрерывной на любом отрезке в рассматриваемом интервале.
