Монотонные последовательности.

Определение: Последовательность {X_n} называется монотонной, если она является либо не убывающей, либо невозрастающей.

Определение: Последовательность {X_n} называется неубывающей (невозрастающей), если все элементы этой последовательности, начиная со второго удовлетворяют неравенству .

Неубывающая и невозрастающая последовательность называются монотонной последовательностью.

Теорема(теорема о сходимости некоторой ограниченной последовательности): Если неубывающая (невозрастающая) последовательность ограничена сверху (снизу), эта последовательность является сходящейся.

Доказательство: Система отрезков { } наз. стягивающейся системой отрезков, если недостающий отрезок в предыдущем и если длина отрезка  0 при n 

Следствии: У всякой стягивающейся системы отрезков существует единственная точка, принадлежащая всем отрезкам.

Число е

Рассмотрим последовательность рациональных чисел n-ый член которой определяется

(2)

Покажем что последовательность n-ый член которой определяется соотношением (2), является сходящейся. Для этого покажем, что эта последовательность является возрастающей и ограниченной сверху.

Используя формулу Бинома – Ньютона соотношение 2 можно представить виде:

=

Используя выражение для числа сочетаний , получим:

=

Перепишем последнее соотношение в виде

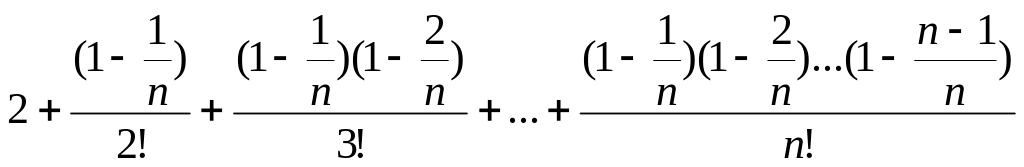= (3)

Используя представление (3), выпишем выражение для (n+1) элементов последовательности (4):

В выражении (3) присутствуют n слагаемых, в выражении (4) – (n+1) слагаемых.

Заметим, что последнее слагаемое в выражении (4) положительное.

Сравним между собой к-ое слагаемое соотношений (3),(4), где к меняется от 2 до n

k-ое слагаемое в соотношении (4) будет иметь вид:

Сравнивая к-ые слагаемые, замечаем, что к-ое слагаемое выражения (3) < k-ого слагаемого выражения (4). Откуда вытекает выполнение неравенства: , т.е. рассматриваемая последовательность является возрастающей.

Покажем, что эта последовательность является ограниченной. Заменим в выражении (3) каждую круглую скобку 1. В результате получим неравенство:

(5)

Используя очевидное соотношение

Используя очевидное неравенство для и оценки (5) получим что

Используя формулу бесконечно убывающей геометрической прогрессии парвую часть представем в виде

Рассматривая последовательность возрастающую и которая ограниченна сверху следовательно она имеет придел. Следуя Леонарду Геллеру этот предел обозначается в виде

Вещественное число

Если последовательность является бесконечно большой то её предел равен бесконечности

Если не является сходящейся то её называют расходящейся.

Функция

Определение: Если каждому значению переменной Х ,принадлежат некоторые области,соответствует одно определённое значение другой переменной Y есть функция от Х,или записи y=f(x),y= (x). ( -независимая переменная)

Определение: Совокупность значений Х,для которого определяются значения функции Y,называются областью определения функции.

Пример:

Определение:

Если функция y=f(x) такова,что большему значению аргумента Х,соответствует наибольшее значение функции,то y=f(x) называется возрвстающей(убывающей).

Если каждое значение Х принадлежит области,соответствующих значений Y,или бесконечно много Y,то функция называется многозиатной.

Способы образования функций.

1)Табличный (выписываются значения аргумента ,и соответствыющие значения ).

2)Графический.