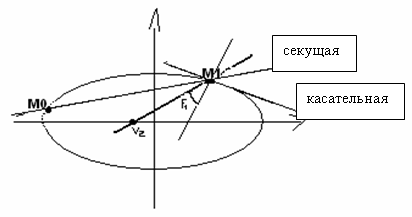
Уравнение касательной к эллипсу

Пусть , лежит на эллипсе, уравнение которой имеет вид . Проведём через точку производную прямую и найдём координаты второй точки пересечения прямой и эллипса. Прямая называется секущей. Если будет двигаться к , следовательно, получится касательная.

Зададим секущую прямую уравнением:

где t-параметр, - координаты направляющего вектора.

Для нахождения точки , подставим координаты прямой в уравнение эллипса.

=>

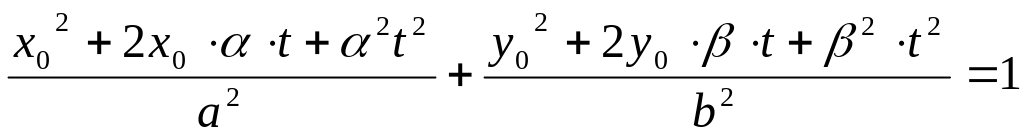
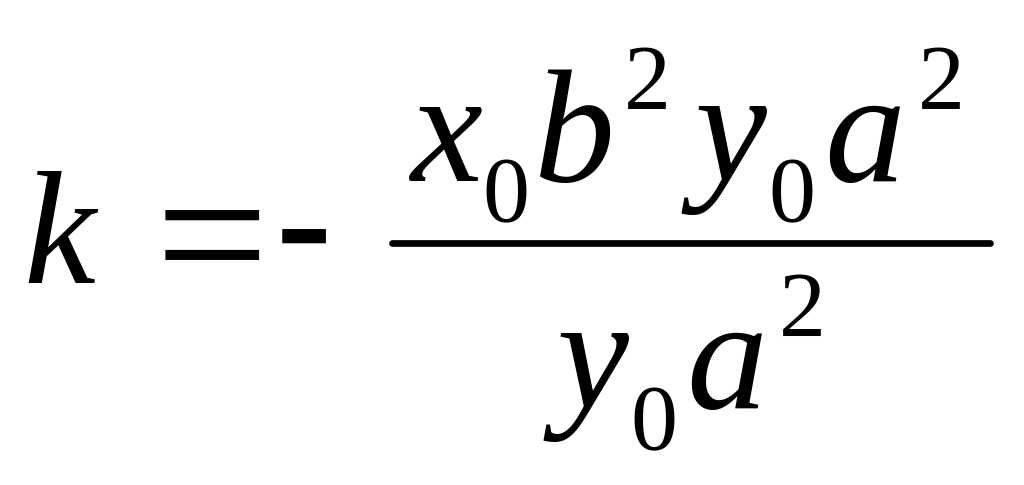
Так как точка лежит на эллипсе, то последнее уравнение можно переписать в виде.

, где к – угловой коэффициент.

вынесем параметр t за скобку.

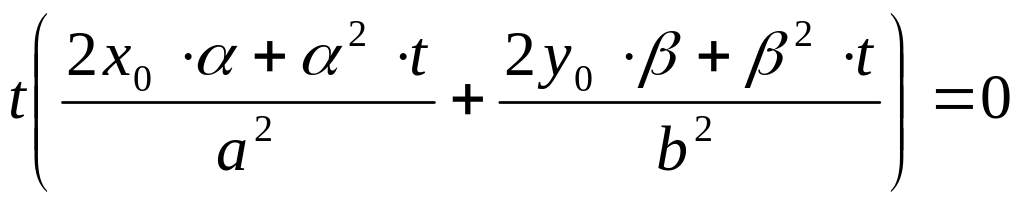
Для определения параметра t, мы должны приравнять каждый множитель к 0. При t=0; получим , приравняв к нулю круглую скобку, найдем координаты точки , для того чтобы точки и совпадали, необходимо потребовать, чтобы значение t=0 обращало в ноль круглую скобку, подставим значение t=0, получим соотношение.

Найдём угловой коэффициент k, определяющий уравнение касательной:

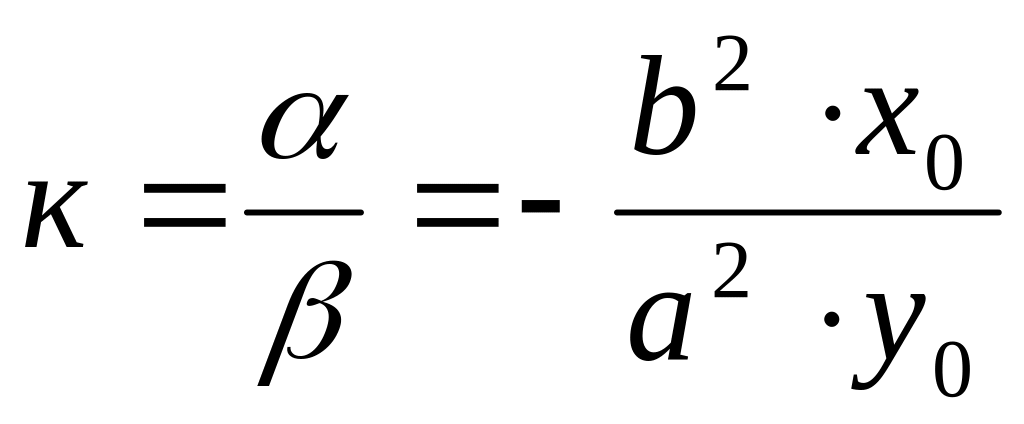
подставляем найденные значения к в уравнение прямой, проходящей через .

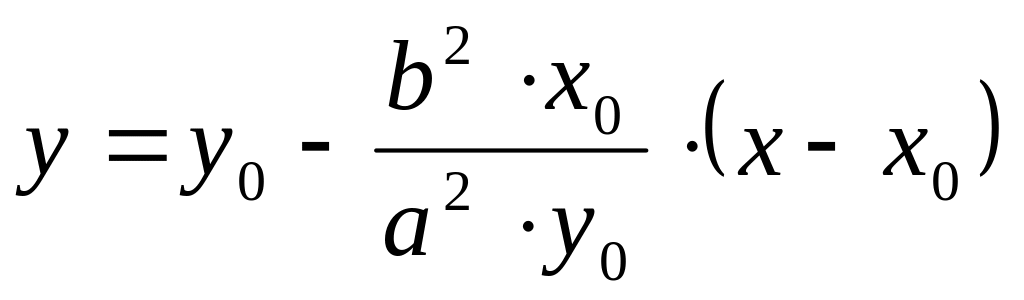-уравнение касательной к эллипсу, проходящее через т.

Обычное уравнение касательной записывается в более симметричном виде. Для этого приводят выражение к общему знаменателю

Замечаем, M₀ лежит на эллипсе, т.е. удовлетворяют уравнению

Уравнение касательной к эллипсу может быть представимо в виде:

- уравнение касательной к эллипсу.

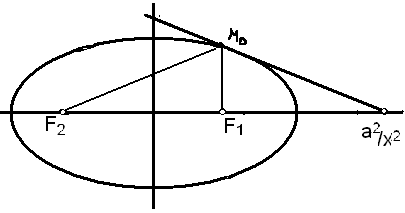
Касательная к эллипсу в точке M₀ (x₀,y₀) есть биссектриса угла, смежного с углом между отрезками, соединяющими эту точку с фокусами.

Гипербола

Определение: Гиперболой называется линия, которая в некоторой, декартовой прямоугольной системе координат определяется каноническим уравнением:

(1)

Из уравнения (1) вытекает, что первая координата точек гиперболы удовлетворяет неравенству . Точки гиперболы расположены, в виде вертикальной полосы, шириной 2а. Гипербола пересекает ось абсцисс в точках (a,0) (-a,0). Эти точки называются вершинами гипотенузы. Величина а называется действительной полуосью гиперболы. Гипербола не пересекается с осью ординат.

Величина b называется минимальной полуосью гиперболы. Координаты x, y входящие в уравнение во вторых степенях, поэтому справедливо 1⁰. Оси координат являются осями симметричными гиперболе, а начальные координаты- центром симметрии гиперболы, для определения формулы гиперболы выпустим из начала координат систему лучей. И исследуем точки пересечения с гиперболой.

1⁰ Оси канонической системы координат гиперболы являются осями симметрии, а начало канонической системы, центром симметрии.

Для исследования формы гиперболы найдем её пересечение с произвольной прямой, проходящей через начало координат. Уравнение прямой возьмем в виде . Абсциссу точек пересечения находится из уравнения :

Это позволит узнать координаты двух точек пересечения.

В силу симметричности достаточно рассмотреть формулу гиперболы в I четверти. Произвольный луч, выходящий из начала координат y=kx. Подставляя точки луча в уравнение гиперболы:

В силу симметрии достаточно проследить за движением первой из точек, при изменении k. Числитель дроби постоянный, а знаменатель принимает наибольшее значение при k=0, следовательно, наименьшую абсциссу имеет точка с координатами (a,0), с ростом k знаменатель убывает и абсцисса х растет бесконечно, когда k приближается к числу b/a. Прямая y=bx/a с угловым коэффициентом b/а не пересекает гиперболу и прямые с большим угловым коэффициентом также больше её не пересекает.

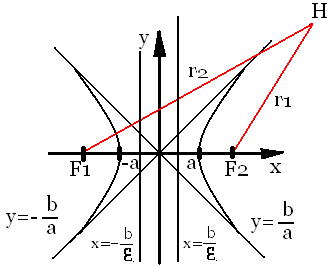
Определение: прямые с уравнениями y=bx/a b y=-bx/a в канонической системе координат называются асимптотами гиперболы. С гиперболой связаны две замечательные точки, называемые его фокусами. Пусть с²=а²+b² и с>0.

Фокусами гиперболы называются точки F₁, F₂ c координатами соответственно (c,0), (-c,0). Отношение называют экстрацентритетом у гиперболы .

2⁰ Тока М лежит на гипотенузе тогда и только тогда, когда разность расстояний до фокусов гипотенузы по абсолютной величине равна 2а.

-эксцентриситетом гипотенузы E>1.С гипотенузой связаны 2 замечательные прямые, называемые её директрисами. Уравнение директрис имеет вид:

3⁰ Точка М лежит на гипотенузе, если отношение расстояний от этой точки до фокуса к расстоянию до соответствующей директрисы равной E .

. Уравнение касательной к гиперболе выводится аналогично уравнению касательной к эллипсу, и имеет вид.