Скалярное произведение векторов в ортогональном базисе.

Пусть задан ортогональный базис .Найдем выражение для скалярного произведения векторов через их координаты

Используя утверждение 2 имеем :

Согласно утверждению 4 , , то приходим к следующему утверждению.

Утверждение 6) Если базис ортонормированный , то скалярное произведение векторов выражается через их компоненты по формуле

Утверждение 6 позволяет написать выражение длины вектора через его компоненты в ортонормированном базисе .

а также выражение угла между векторам

Используя формулу для длины вектора можно вычислить расстояние между точками , если заданы их координаты в декартовой прямоугольной системе координат.

Пусть , тогда расстояние между ними равно

Векторное произведение.

Определение: Упорядоченная тройка некомпланарных векторов называется правоориентированной , если из конца третьего вектора кротчайший поворот о первого ко второму будет против часовой стрелки в противнои случае тройка называется левоориентированной .

Определение: Векторным произведением векторов называется вектор ,удовлетворяющий следующим условиям:

1) , где - угол между векторами .

2)вектор c ортоганален к векторам а и b.

3)вектора a,b,c образуют новую тройку векторов.

Векторное произведение образуется в виде [a,b].Если один из сомножителей равен 0,то векторное произведение есть нулевой вектор.

Пример: Пусть правый ортогорированный вектор.

Утверрждение 7: Векторное умножение антикоммутативно,т.е

Доказательство: Изменив порядок сомножителей, меняем ориентацию тройки векторов и изменяя величины векторов.

Смешанные произведения векторов.

Определение: число (a[b,c]) называется смешанным произведением векторов a,b,c и обозначается [a,b,c].

Утверждение 8: Смешанное произведение некомпланарных векторов a,b,c ,по модулю равно объёму параллепипеда, построенного на сомножителях, оно положительно если тройка векторов a,b,c-правая, и отрицательно, если оно левая.

Объём парараллепипеда, построенного на векторах a,b,c равен произведению площади и основания( ),умноженного на высоту( ), поэтому, V=

Если ортогонален правому базису, то ( )=1

Утверждение 9: Смежное произведение равно 0,тогда итолько тогда когда сомножители компланарны.

Утверждение 10: Смежное произведение левой тройки векторов a,b,c удовлетворяет свойству линейности.

+ +

+М )+М

Доказательство:Сравнивая ориентации трех векторов, получим: = - - - (*)

Применим линейность скалярного произведения к выражению: = +М

Из равенства (*) следует аналитическое тождество, для остальных сомножителей.

Утверждение 11: Линейность векторной производной. Для местных векторов а,b,c и некоторых чисел ,имеет место равенство: =

Доказательство: Для доказательства воспользуемся линейностью смешанного произведения по второму сомножителю:

= - это равенство имеет место при всех а. Выберем ортогонированный базис и .Подставим вместо а, последовательно каждый вектор базиса, в силу утверждений 1,2.3 получим равенство всех компонентов векторов и ,отсюда ,требуемое равенство векторов.

Выражение векторного и смешанного произведения через координаты сомножителей.

Пусть правый ортогональный базис - координаты вектора - координаты вектора согласно утверждению 11 получим.

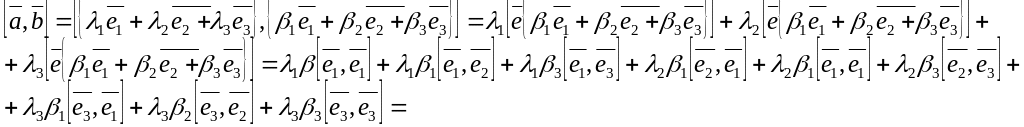
Учитывая, что , , Получим:

Пусть тогда смешанное произведение: