Евклидово пространство

Определение: Линейное пространство Е называется евклидовым , если выполняются два требования :

1)В пространстве Е определена операция , ставящая в соответствие каждой паре элементов некоторое вещественное число – эта операция называется скалярным произведением .

2)скалярное произведение удовлетворяет следующим аксиомам.

1] коммутативность , симметричность .

2] дистрибутивность

3]

4] причем равенство достигается только в том случае , когда нулевой.

Отметим , что скалярное произведение в алгебре по способу определения отличаются от скалярного произведения в геометрии, где

В геометрии рассматривается пространство размерности не более 3-х и понятия длины вектора и угла между векторами вводится до определения скалярного произведения. В алгебре понятие скалярного произведения понимается как операция удовлетворяющая 4-м аксиомам, и только потом вводится понятие длинны вектора = и понятием угла cos ,и эти понятия распространяются на пространства любой размерности.

Свойства скалярного произведения

1) Неравенство Коши-Буняковского:

Для евклидового пространства имеет место соотношение:

(1) неравенство Коши-Буняковского.

Доказательство: Выражение .Согласно 4-у свойству скалярное произведение будет использоваться 1-е,2-е,3-е свойства. Преобразуем скалярное произведение:

-

A ,где А,В,С - некоторые числа.

Видим, что в левой части стоит квадратный трёхчлен, ветви которого направлены вверх, неравенство выполнится в том случае, если дискриминант квадратного трёхчлена

Возвращаясь к скалярному произведению, получим

Что и требовалось доказать.

2)Матрица Грамма.

Пусть - некоторый базис евклидова пространства E. Возьмём два произвольных вектора . Разложим вектора по базису.

Найдём представленное скалярное произведение векторов x,y в заданном базисе Е.

= согласно аксиоме о дистрибутивности ,получим =

Представим элемент столбца( ,воспользовавшись разложением вектора y по координатам, получим( =

Подставляя, найдем соотношение в скалярном произведении векторов ,определим в виде матричного соотношения:

=( (2)

Матрица стоящая в (2), называется матрицей Грамма. Исходя из , замечаем, что матрица Грамма симметрична относительно главной диагонали. Матрица Грамма составлена из скалярных произведений базисных векторов.

3)Изменение матрицы Грамма при переходе к новому базису.

Наряду со старым базисом , рассмотрим новый базис . Связь между базисами устанавливается с помощью матрицы перехода Т. = Т. Матрица перехода Т, позволяет установить связь между старыми и новыми координатами. (3)

Транспонируя соотношение для столбца Х. = (4). Подставляя выражения (3) и (4) во (2), получим: = (5)

Матрица Грамма в новом базисе равна: .

Определение: два вектора называются ортогональными, если их скалярное произведение равно нулю.

Из определения ортогональности следует, что нулевой вектор ортогонален любому вектору.

Определение: система векторов называется ортогональной, если каждая пара этих векторов ортогональна между собой.

Теорема: ортогональная система не нулевых векторов, линейно независима.

Доказательство: пусть вектора ортогональны между собой, и нулевой вектор не содержится в этой системе векторов. Составим линейную комбинацию векторов и приравняем её к нулю.

(6)

Теорема будет доказана, если покажем что уравнение (6) имеет место только при нулевых коэффициентах, рассмотрим скалярное произведение вектора из заданной системы векторов на соотношение(6).

0 0 0

в силу ортогональности системы векторов, получаем , скалярный квадрат не равен нулю, следовательно .

В силу произвольности выбора , видим что все коэффициенты соотношения (6) равны нулю.

Теорема доказана.

Определение: вектор называется нормированным, если его скалярный квадрат равен единице, .

Система векторов называется ортонормированной, если все вектора этой системы нормированы и попарно ортогональны. В ортогональном базисе, матрица Грамма принимает наиболее простой вид.

i . Т.о. матрица Грамма в ортонормированном базисе.

G= единичная.

Пример: Пусть заданы в ортонормированном базисе

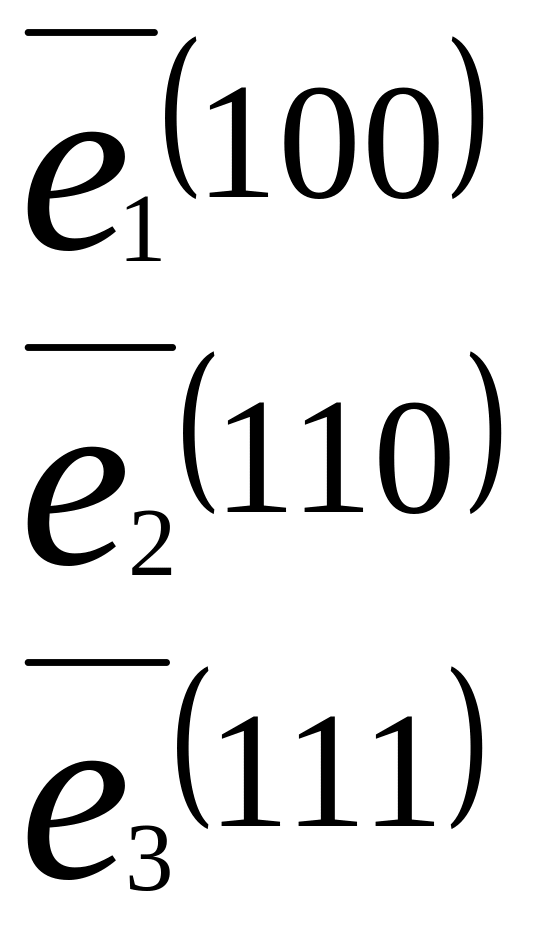
Найти скалярное произведение векторов(x;y).

x= y=

Решим задачу с помощью матрицы Грамма.

G= ( )=(111) ( )=(111)