Отношение эквивалентности

Одним из важных математических понятий является понятие множества. Множества принято обозначать заглавными буквами A,B,C, … Элементы множества принято обозначать строчными буквами a,b,c,… . Принадлежность элемента а множеству А, обозначается в виде a  A. Конечные множества могут быть заданы перечислением всех своих элементов, либо с помощью указания характеристического свойства, позволяющего определить принадлежность элемента к множеству.

Множество состоящее из двух элементов 1, 2 может быть задано перечислением элементов:

A={1,2} ;

либо указанием характеристического свойства

A={x | x²-3x+2=0}

Последняя запись означает, что множество А состоит из элементов х, являющихся решением уравнения x²-3x+2=0.

Часто приходится иметь дело с более сложными множествами. Пусть заданы множества X,Y. Пара элементов (x,y) такая, что x  X, y  Y, взятая в указанном порядке называется упорядоченной парой.

Две пары (x₁;y₁) и (x₂;y₂) равны, тогда и только тогда, когда x₁=x₂, y₁=y_2.

Если множество X и Y конечны, множество X состоит из n-элементов и множество Y состоит из m-элементов то число упорядоченных пар равно произведению n m. Все упорядоченные пары можно представить в виде прямоугольной таблицы вида:

Y X					...
					...
					...
					...
...	...	...	...	...	...	...
					...

Число ячеек в этой таблице n m.

Определение: Совокупность всех упорядоченных пар (x,y) построенных для множеств X,Y называется Декартовым произведением множеств.

Декартово произведение обозначается:

X Y={(x;y)│xX yY}.

Аналогично образом можно ввести декартовое произведение трёх множеств.

X Y Z={(x,y,z) │ xX, yY,zZ }.

Если множества X, Y, Z конечны и состоят из n, m, k элементов то количество упорядоченных троек равно произведения чисел n×m×k. Поскольку декартово произведение множеств можно рассматривать как пару образованную из двух множеств, так если A=X×Y, X×Y×Z=(X×Y)×Z=A×Z. В общем случае, если имеется n-множеств , тогда можно записать Декартово произведение этих множеств .

Д екартово произведение в этом случае будет состоять из упорядоченного набора n-элементов. Если эти множества конечны и состоят из m-элементов, то число упорядоченных наборов будет равно

Рене Декарт (1596-1650) предложил изображать произведение двух множеств в виде пересекающихся прямых.

Пример:

Пусть множество X=R и множество Y=R , множество R принято изображать числовой прямой тогда декартово произведение совпадает плоскостью

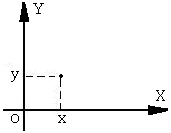
В этом случае упорядоченная пара (x;y) изображается точкой на плоскости. В рассматриваемом примере упорядоченную пару принято обозначать двухмерным вектором =(x,y) . Рассмотрим случай если , то .

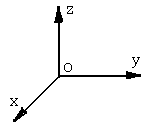
Упорядоченной тройкой в данном случае называется трёхмерный вектор .

Упорядоченная тройка определяет точку в трёхмерном пространстве. Если ( i меняется от 1 до n ),то - декартово произведение и элементами этого множества будут являться упорядоченные пары (x₁, x₂, … , x_n), который называются n-мерным вектором.

В школьном курсе математики изучаются понятия «больше» и «меньше». Обобщением этих понятий «>», «<» является понятием бинарного отношения.

Определение: Для любых двух множеств X, Y всякое подмножество называется бинарным отношением между X, Y (или просто на X, если X = Y).

Другими словами, чтобы задать бинарное отношение, нужно указать все упорядоченные пары, удовлетворяющие заданному свойству. Традиционно, вместо записи (x, y) , в случае бинарного отношения используют x y.

Изобразим бинарные отношения x < y на множестве R.

x – y < 0;

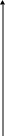
x – y = 0; y y = x

y = x.

M 1

-1 -1 x

подмножество образуется из точек принадлежащих заштрихованной области.

Пример:

Заданное бинарное отношение изобразить на декартовой диаграмме.

x y  = {(x, y) | x² + 4 y² ≤ 1} точка (x,y)  , если ее координаты удовлетворяют неравенству x² + 4 y² ≤ 1

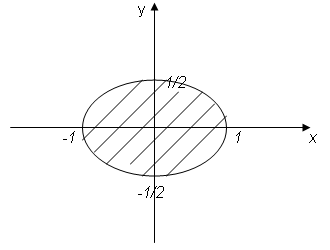
уравнение границ области будет иметь вид x² + 4 y² ≤ 1

гнаница разбивает плоскость на две части. Для определения нужной области выберем произвольную точку, например О(0,0) и подставим ее в левую часть неравенства, т.к. 0 + 0 = 0 ≤ 1, то необходимо заштриховать область, содержащую точку О(0,0).

Бинарные отношения на конечном множестве X можно представить при помощи особых чертежей, состоящих из точек, соединённых стрелками. Такие чертежи называются графами.

Пример:

На множестве X = {3, 4, 5, 6, 8} задать бинарные отношения «больше», «>» на единицу 1, «меньше» в 2 раза.

а) = {(4, 3), (5, 3), (6, 3), (8, 3), (5, 4), (6, 4), (8, 4), (6, 5), (8, 5), (8, 6)}-бинарное отношение больше

граф бинарного отношения больше. Каждая упорядоченная пара, принадлежащая множеству изображается стрелкой и проведенной от первого числа ко второму

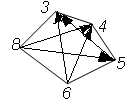
в) = {(4, 3), (5, 4), (6, 5)} – бинарное отношение, больше на единицу.

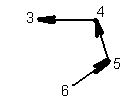
c) = {(3,6);(4,8)} – бинарное отношение, меньше в два раза.

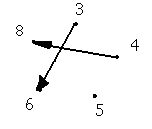
Если упорядоченная пара (a,a), принадлежит бинарному соотношению, то ее следует изображать петлёй.