2. Краткие сведения из теории вероятностей ...

график симметричен относительно оси ординат, из этого следует, что эти точки расположены на одинаковом расстоянии от нуля.

1-р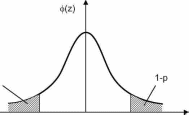

Z1-_P zp Z

Рис. 2.4. Квантиль стандартного нормального распределения

Зная квантиль z_p порядка р нормированного нормального закона распре­деления (M_z = 0 и cr_z ² = 1), всегда можно найти квантиль х_р соответствующего порядка р для нормального распределения с произвольными параметрами М_х\л о-х² .

Поскольку

^х< °_х &_х

Х-М х -М_х х -М_х х -М_х F(x_p)=P(X<x_p)=P( < )=P(Z< ) = Ф( )=Р=Ф(г ),

&_х

&_х

то

х — М_х

°_х

z_p и, следовательно,

^Xp⁼Mc^+Zp^(Jx.

(2.32а)

В ряде случаев важно знать вероятность того, что случайная величина X, подчиняющаяся нормальному закону распределения, не будет отличаться от своего математического ожидания М_х больше чем на величину ±5 = ео_х (см.рис.2.3,г).

Р(М_Х —8<Х<М_Х +S)=P

M_x—scr_x—M_x Х—М_х М_х+£сг_х—М_у

<

a

a

<

°_х

=P(_re<Z<+s)

2 2

s z -e z

1 -2 1 "2

\e ²dz—= \e ²dz =ф(е)-ф(-е) =

42т_

33

2. Краткие сведения из теории вероятностей ...

= Ф(е)-(1-Ф(е)) = 2Ф(е)-1. (Z33)

Так, при 8 = сг_х(£=1) получаем, что P(M_x+а_x<X<M_x-а_x) = 2Ф(1)-1, а

поскольку по таблицам (например, см. табл. [11) Ф(1) = 0,84135 (или в Microsoft Excel НОРМРАСП(1;0;1;ИСТИНА) = НОРМСТРАСП(1) = 0,84135), то для слу­чайной величины с нормальным законом распределения вероятность того, что она примет такое значение, которое не будет отличаться от ее математическо­го ожидания более чем на одно среднее квадратическое отклонение, равна 20,84135-1=0,68. Иными словами, при нормальном распределении примерно 2/3 всех значений случайной величины (отклика) лежит в интервале М_х ± а_х.

Аналогично можно подсчитать, что интервалу М_х ± 1,96сг_х « М_х ± 2а_х со­ответствует вероятность 0,95 (Ф(1,96) = 0,975002), а интервалу М_х ± За_х - 0,997 (Ф(3) = 0,99865). Отметим дополнительно, что 90% значений случайной вели­чины лежат в диапазоне М_х ± 1,64а_х (Ф(1,64) = 0,949497).

Следовательно, отличие какого-либо из значений случайной величины с нормальным законом распределения от ее математического ожидания не превосходит утроенного среднего квадратичного отклонения с вероятно­стью 0,997. Это свойство в математической статистике носит название «пра­вило трех сигм».

Чем больше величина интервала М_х ± 8, тем с большей вероятностью случайная величина X попадает в этот интервал.

Рассмотрим небольшой пример.

Пример 2.2. Предположим, что математическое ожидание содержания кремния в чугуне равно M_Si=0,6%, а среднеквадратичное отклонение a_Si=0,15%. В этом случае мы можем быть уверены в том, что величина фактически изме­ренного значения процентного содержания кремния в чугуне будет находиться в интервалах:

0,6 ± 1,000,15 = 0,6±0,15 с вероятностью 0,68;

0,6 ± 1,640,15 = 0,6±0,25 с вероятностью 0,90;

0,6 ± 1,960,15 = 0,6±0,29 с вероятностью 0,95;

0,6 ± 3,000,15 = 0,6±0,45 с вероятностью 0,997,

34